Презентация - Построение и расчет размерных цепей
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 83%
- Слайдов: 51
- Просмотров: 6455
- Скачиваний: 3093
- Размер: 2.89 MB
- Онлайн: Да
- Формат: ppt / pptx
Примеры похожих презентаций
 Пропорции и построение головы человека 6 класс
Пропорции и построение головы человека 6 класс Построение и исследование графиков функций с использованием программного обеспечения компьютеров
Построение и исследование графиков функций с использованием программного обеспечения компьютеров Пропорции и построение фигуры человека 7 класс
Пропорции и построение фигуры человека 7 класс Алгоритмы Прима и Крускала построения остовного связного дерева минимального веса
Алгоритмы Прима и Крускала построения остовного связного дерева минимального веса Законы построения раппортной композиции. Поиск мотива из модулей
Законы построения раппортной композиции. Поиск мотива из модулей Задачи на построение сечений
Задачи на построение сечений Построение
Построение
Слайды и текст этой онлайн презентации
Слайд 1
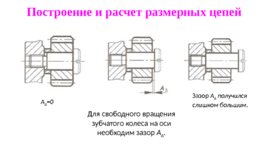
Построение и расчет размерных цепей Для свободного вращения зубчатого колеса на оси необходим зазор А . А 0 Зазор А получился слишком большим.
Слайд 2
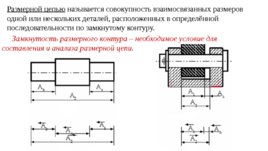
Размерной цепью называется совокупность взаимосвязанных размеров одной или нескольких деталей, расположенных в определённой последовательности по замкнутому контуру. Замкнутость размерного контура – необходимое условие для составления и анализа размерной цепи.
Слайд 3

Все размеры (звенья) размерной цепи разделяют на составляющие и замыкающее (исходное). Все составляющие звенья цепи делят на : Увеличивающие звенья – те, с увеличением размера которых замыкающее звено увеличивается; Уменьшающие звенья – те, с увеличением размера которых замыкающее звено уменьшается. Замыкающее звено – размер (или звено), который получается в размерной цепи последним при обработке или сборке. В некоторых случаях замыкающее звено является исходным, т.е. его точность известна и исходя из которой рассчитывается точность составляющих звеньев.
Слайд 4

Правила построения размерных цепей Перед тем как построить размерную цепь, следует выявить замыкающее звено, которое, определяет нормальное функционирование механизма или обеспечивает точность изготовления изделия. Размер или предельные отклонения замыкающего звена назначают или рассчитывают исходя и условий работы и (или) требуемой точности. Размер и предельные отклонения А принимаются такими, что обеспечат свободное вращение зубчатого колеса и при этом его смещение вдоль оси будет минимальным.
Слайд 5

Цепь должна быть замкнута; Размер любого звена сборочной цепи должен относится к элементам одной и той же детали (исключением является замыкающее звено, которое всегда соединяет элементы разных деталей); Цепь должна быть проведена наикратчайшим способом, т.е. деталь своими элементами должна входить в размерную цепь только один раз. При построении размерных цепей следует руководствоваться их основными свойствами:
Слайд 6
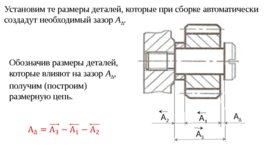
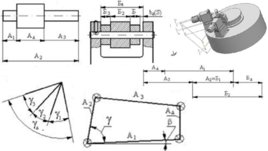
А 2 А 1 А 3 А Установим те размеры деталей, которые при сборке автоматически создадут необходимый зазор А . Обозначив размеры деталей, которые влияют на зазор А , получим (построим) размерную цепь.
Слайд 7

Правила построения схемы размерной цепи: Выбирают базовую плоскость, которую обычно совмещают с одним из краёв замыкающего звена; Замыкающее звено всегда направляют от базы и совместно с ним выбирают направление составляющих звеньев. Исходя из графика размерной цепи, сонаправленные с замыкающим составляющие звенья являются уменьшающими (А 3 , А 4 , А 5 ), а противоположно направленные – увеличивающее (А 1 , А 2 ).
Слайд 8
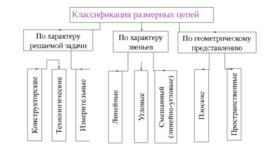
По характеру решаемой задачи По характеру звеньев По геометрическому представлению Классификация размерных цепей
Слайд 9
Слайд 10
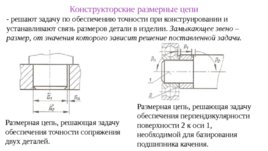
Конструкторские размерные цепи - решают задачу по обеспечению точности при конструировании и устанавливают связь размеров детали в изделии. Замыкающее звено – размер, от значения которого зависит решение поставленной задачи. Размерная цепь, решающая задачу обеспечения точности сопряжения двух деталей. Размерная цепь, решающая задачу обеспечения перпендикулярности поверхности 2 к оси 1, необходимой для базирования подшипника качения.
Слайд 11
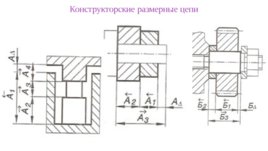
Конструкторские размерные цепи
Слайд 12
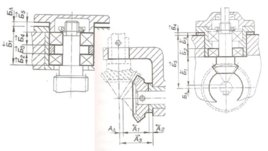
Слайд 13
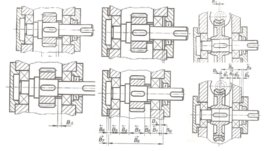
Слайд 14

Технологические размерные цепи - решают задачу по обеспечению точности при изготовлении машин и устанавливают связь размеров деталей на разных этапах технологического процесса. Замыкающее звено – размер, точность которого обеспечивается технологическим процессом. 1. Деталь с размерами, которые следует выдержать при изготовлении. 2. Последовательность получения размеров. 3. Построенная технологическая размерная цепь (на основании предложенного маршрута обработки.
Слайд 15
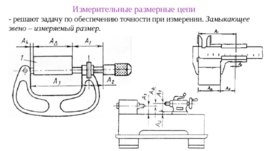
Измерительные размерные цепи - решают задачу по обеспечению точности при измерении. Замыкающее звено – измеряемый размер.
Слайд 16

При решении размерных цепей рассматриваются две задачи – прямая и обратная, отличающиеся последовательностью расчёта. Прямая задача : по заданным предельным размерам замыкающего звена определить номинальные размеры, допуски и предельные отклонения составляющих звеньев (применяется при проектировочном расчёте размерной цепи). Обратная задача : по установленным номинальным размерам, допускам и предельным отклонениям составляющих звеньев определить номинальный размер, допуск и предельные отклонения замыкающего звена (применяется в тех случаях, когда требуется проверить соответствие допуска замыкающего размера допускам соответствующих размеров, проставленных на чертеже, т.е. выполнить проверочный расчёт ).
Слайд 17

Обеспечение полной взаимозаменяемости – назначаются такие требования точности составляющих звеньев, что при любом их сочетании обеспечивается заданная точность замыкающего звена. Обеспечение неполной взаимозаменяемости – требования к точности составляющих звеньев назначаются таким образом, что возникает необходимость, например, дополнительно обрабатывать отдельные звенья, либо использовать дополнительные детали, такие как прокладки, клинья, уплотнения и т.п. (компенсаторы). Для решения обеих задач используют два подхода :
Слайд 18

Методы достижения заданной точности замыкающего звена (решение размерных цепей): Метод полной взаимозаменяемости; Вероятностный метод; Метод пригонки; Метод регулирования; Метод групповой взаимозаменяемости.
Слайд 19

Способы расчёта размерных цепей: Расчёт на максимум-минимум , при котором учитываются только наибольшие и наименьшие отклонения составляющих звеньев; Вероятностный расчёт , при котором не учитываются сочетания предельных отклонений звеньев, а учитывается то, что сочетания действительных размеров звеньев носят случайный характер и вероятность появления при сборке самых неблагоприятных сочетаний звеньев мала. Поэтому можно расширить поля допусков составляющих звеньев, задаваясь некоторым допустимым процентом выхода за пределы допуска замыкающего звена.
Слайд 20

Основные соотношения размерных цепей
Слайд 21

Основные соотношения размерных цепей
Слайд 22
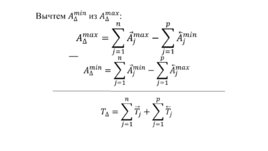
Слайд 23

Слайд 24

Слайд 25

1. Метод полной взаимозаменяемости – метод, при котором требуемая точность замыкающего звена размерной цепи получается при любом сочетании размеров составляющих звеньев. При этом предполагается, что в размерной цепи одновременно могут оказаться все звенья с предельными значениями в любом из двух наиболее неблагоприятном сочетании – все увеличивающие звенья с верхними предельными отклонениями, а уменьшающие с нижними и наоборот. Такой метод называется методом расчёта на максимум-минимум.
Слайд 26

2. Метод неполной взаимозаменяемости – метод, при котором требуемая точность замыкающего звена размерной цепи получается не при любых сочетаниях, а при ранее обусловленной части сочетаний размеров составляющих звеньев. Метод исходит из предположения, что сочетание действительных размеров составляющих звеньев в изделии носит случайный характер и вероятность того, что все звенья с самыми неблагоприятными сочетаниями окажутся в одном изделии, весьма мала. Метод расчёта, который учитывает рассеяние размеров и вероятность их различных сочетаний вероятностный метод.
Слайд 27

3. Метод пригонки – метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением размера компенсирующего звена путём снятия с компенсатора слоя материала. Суть метода в том, что допуски на составляющие звенья назначаются по экономически приемлемым квалитетам, а получающийся у замыкающего звена избыток поля рассеяния при сборке устраняют за счёт компенсатора. Смысл расчёта – определение припуска на пригонку с наименьшим объёмом пригоночных работ. Роль компенсатора обычно выполняет деталь, наиболее доступная при сборке-разборке механизма, несложная по конструкции и неточная (прокладки, шайбы, простановочные кольца и т.п.).
Слайд 28

4. Метод регулирования – метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением компенсирующего звена без снятия слоя материала. Суть метода в том, что избыток поля рассеяния замыкающего звена устраняют путём подбора компенсатора из некоторого количества компенсаторов, заранее изготовленных с различными размерами. Смысл расчёта – определение наименьшего количества компенсаторов в комплекте.
Слайд 29

5. Метод групповой взаимозаменяемости – метод, при котором требуемая точность замыкающего звена размерной цепи достигается включения в неё составляющих звеньев, принадлежащих к одной из групп на которые они предварительно разбиты. Сущность метода групповой взаимозаменяемости заключается в изготовлении деталей со сравнительно широкими технологически выполнимыми допусками, выбираемыми из соответствующих стандартов, сортировке деталей на равное число групп с более узкими групповыми допусками и сборке их (после комплектования) по одноименным группам. Такую сборку называют селективной.
Слайд 30
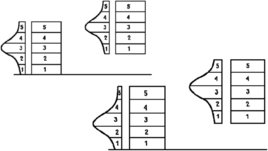
Слайд 31
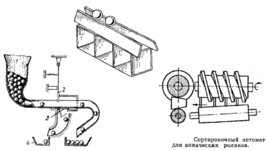
Слайд 32

При выборе метода нужно учитывать следующее: Метод, полной взаимозаменяемости применяется в индивидуальном или мелкосерийном производстве или в случае особо ответственных изделий; Вероятностный – при среднесерийном и массовом производстве; Метод пригонки не рекомендуется, т.к. велики затраты при проведении пригоночных работ; Метод групповой взаимозаменяемости чаще применяется в РЦ высокой точности с небольшим числом составляющих звеньев; Метод регулирования широко применяется в РЦ высокой точности с большим числом составляющих звеньев При использовании стандартных узлов ( типа подшипники качения ) допуски на них постоянны и соответствуют стандартам.
Слайд 33

Понятия об измерении и контроле Измерение – нахождение значения физической величины опытным путём с помощью специальных технических средств – средств измерений, с допустимой погрешностью. Контроль – это измерение, в процессе которого определяют, находится ли значение измеряемой величины в заранее установленных для нее пределах. Единство измерений – такое состояние измерений, при котором результаты измерений выражаются в узаконенных единицах, а их погрешность с заданной вероятностью не выходит за пределы допустимой.
Слайд 34

Измерение – это нахождение значения физической величины (ФВ) опытным путем с помощью специальных технических средств. В этом определении содержатся главные признаки понятия «измерение»: измерять можно только ФВ; измерение требует проведение опытов; для проведения данных опытов требуется специальные технические средства, проводимые во взаимодействии с объектом, которые называются средствами измерений ; результатом измерений является значение ФВ . Значение ФВ должно быть не просто числом, а числом именованным, т.е. результат должен быть выражен в определенных единицах, принятых для данной величины.
Слайд 35
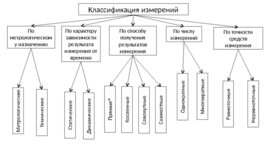
Классификация измерений По метрологическому назначению По характеру зависимости результата измерения от времени По способу получения результатов измерения По числу измерений По точности средств измерения
Слайд 36
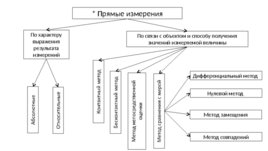
Прямые измерения По характеру выражения результата измерений По связи с объектом и способу получения значений измеряемой величины Дифференциальный метод Нулевой метод Метод замещения Метод совпадений
Слайд 37

Метрологические измерения выпол няются при помощи эталонов с целью воспроизведения единиц ФВ для передачи их размера рабочим средствам измерений, например, измерения при поверке. Технические изме рения проводятся рабочими средствами измерений, как правило, в производственных условиях. К статическим измерениям относятся измерения ФВ, прини маемой в соответствии с конкретной измерительной задачей за не изменную на протяжении времени измерения. Динамические измерения — это измерения изменяющейся по размеру ФВ. Примером динамических измерений является измере ние термопарой температуры печи при закалке детали с фиксацией результатов по шкале самописца.
Слайд 38

Прямое измерение — измерение, при котором искомое значе ние ФВ находят непосредственно по показаниям средства измере ний. Косвенное измерение — измерение, при котором искомое зна чение ФВ определяют на основании результатов прямых измерений других ФВ, функционально связанных с искомой величиной. Дру гими словами, искомое значение ФВ рассчитывают по формуле, а значения величин, входящих в формулу, получают прямыми изме рениями. Примерами косвенных измерений могут служить опреде ление объема тела по прямым измерениям его геометрических раз меров, определение угла конуса по прямым измерениям большого и малого основания и расстояния между ними и т.п.
Слайд 39

Совокупные измерения — измерения одновременно нескольких одноименных величин, при которых искомые значения величин находят решением системы уравнений, полученных при измерении этих величин в различных сочетаниях. Примером совокупных изме рений может служить нахождение значений массы отдельных гирь набора по известному значению массы одной из гирь (сравнивая массы различных сочетаний гирь, получают систему уравнений, из решения которой находят массу каждой из гирь, входящих в набор). Совместные измерения — одновременные измерения двух или нескольких разнородных величин для установления зависимости между ними. Примером совместных измерений может служить ряд одновременных прямых измерений длины тела и его температуры для установления зависимости размера от температуры.
Слайд 40

Однократное измерение выпол няется один раз. Например, измерение конкретного момента време ни по часам. Многократное измерение предусматривает измерение ФВ одного и того же размера, результат которого получен из не скольких следующих друг за другом измерений, т.е. состоит из ряда однократных измерений. Равноточные измерения — это ряд измерений какой-либо ве личины, выполненных одинаковыми по точности средствами изме рений в одних и тех же условиях с одинаковой тщательностью. Неравноточные измерения — ряд измерений какой-либо вели чины, выполненных различающимися по точности СИ и в различ ных условиях.
Слайд 41

Абсолютное измерение основано на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Понятие «абсолютное измерение» применя ется как противоположное понятию «относительное измерение» и рассматривается в качестве определения величины в ее единицах. Примером абсолютных измерений может служить нахождение штангенинструментом длины или диаметра детали в миллиметрах, дав ления манометра в паскалях и т.п. Относительное измерение — это измерение отношения величины к одноименной величине, играющей роль единицы, или измерение величины по отношению к одноименной величине, принимаемой за исходную. Примером относительного измерения является измерение линейного размера детали с помощью оптиметра, настроенного по концевым мерам длины.
Слайд 42

Контактный метод измерений основан на том, что чувствительный элемент прибора приводится в контакт с объектом измерений. Например, измерение диаметра с помощью микрометра. Бесконтактный метод измерений состоит в том, что чувствительный элемент прибора не приводится в контакт с объектом измерений. Например, измерение параметров резьбы с помощью инструментального микроскопа.
Слайд 43

При измерении по методу непосредственной оценки искомое значение величины определяют непосредственно по отсчетному устройству средства измерений, которое проградуировано в соответ ствующих единицах. Измерения этим методом проводятся быстро и просто и не требуют высокой классификации оператора. Метод сравнения с мерой — метод измерений, при котором изме ряемую величину сравнивают с величиной, воспроизводимой мерой (например, при использовании в качестве меры гири определенной массы). Отличительной чертой методов сравнения является непосред ственное участие меры в процедуре измерения, в то время как в методе непосредственной оценки мера в явном виде при измерении не при сутствует, а ее размеры перенесены на отсчетное устройство (шкалу) средства измерений заранее, при его градуировке. Обязательным в методе сравнения является наличие сравнивающего устройства .
Слайд 44

При использовании метода сравнения с мерой результат изме рения либо вычисляют как сумму значения используемой для срав нения меры и показания измерительного прибора, либо принимают равным значению меры. Метод сравнения с мерой имеет ряд разно видностей; При дифференциальном методе измеряемую величину х срав нивают с однородной величиной х м , имеющей известное значение, незначительно отличающееся от значения измеряемой величины, при котором измеряют разность между этими двумя величинами.
Слайд 45
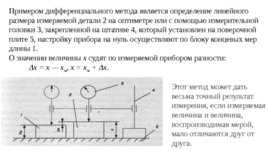
При мером дифференциального метода является определение линейного размера измеряемой детали 2 на оптиметре или с помощью измери тельной головки 3, закрепленной на штативе 4, который установлен на поверочной плите 5, настройку прибора на нуль осуществляют по блоку концевых мер длины 1. О значении величины х судят по измеряемой прибором разно сти: Δх х — х м , х х м Δх . Этот метод может дать весьма точный результат измерения, если измеряемая величина и величина, вос производимая мерой, мало отличаются друг от друга.
Слайд 46
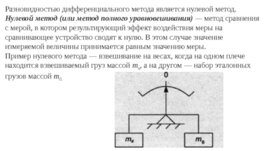
Разновидно стью дифференциального метода является нулевой метод. Нулевой метод (или метод полного уравновешивания) — метод сравнения с мерой, в котором результирующий эффект воздействия меры на сравнивающее устройство сводят к нулю. В этом случае значение измеряемой величины принимается равным значению меры. Пример нулевого метода — взвешивание на весах, когда на одном плече находится взвешиваемый груз массой m x , а на дру гом — набор эталонных грузов массой m 0.
Слайд 47

Метод замещения заключается в том, что измеряемую величи ну замещают в измерительной установке некой известной величи ной, воспроизводимой мерой. Преимущество метода замещения со стоит в том, что измеряемую величину и величину, воспроизводимую мерой, включают последовательно одну за другой в одну и ту же часть измерительного прибора, благодаря чему искомое значение величины определяется по отношению показаний прибора, что спо собствует значительному снижению погрешности измерений. При мер метода замещения — взвешивание на пружинных весах в два приема. Вначале на чашу весов помешают взвешивае мую массу и отмечают положение указателя весов; затем массу m x замещают массой гирь, подбирая ее так, чтобы указатель весов устанавливался точно в том же положении, что и в первом случае. При этом т х m 0 .
Слайд 48

В методе совпадений разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов. По принципу метода совпадений построен нониус, входящий в состав ряда изме рительных приборов, например, штангенинструментов. При выборе метода измерения необходимо добиваться, чтобы погрешность метода измерения, обусловленная несовершенством принятых модели и метода измерения, заметно не сказывалось на результирующей погрешности измерения. Как правило, методическая погрешность не должна превышать 30% суммарной погрешности из мерения. При выборе метода измерения необходимо учитывать и экономические соображения: чрезмерное завышение точности ме тода измерения, как правило, приводит к необоснованным затратам.
Слайд 49
Слайд 50

Слайд 51
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
