Презентация - Основы гидравлики (для бакалавров)

Основы гидравлики (для бакалавров)

Предмет гидравлики, как науки. Гидростатика и гидродинамика

ОСНОВЫ ТЕОРИИ ГИДРАВЛИЧЕСКИХ И АЭРОДИНАМИЧЕСКИХ РАСЧЕТОВ ОСНОВНЫЕ ПОНЯТИЯ ГИДРАВЛИКИ Гидравлика - наука, изучающая законы равновесия и движения жидкостей, а также взаимодействия жидкостей с соприкасающимися с ними неподвижными или движущимися твердыми телами. ЧТО ТАКОЕ ЖИДКОСТЬ? (ОПРЕДЕЛЕНИЕ ЖИДКОСТИ) Жидкость - физическое тело, обладающее свойствами текучести и легко изменяющее свою форму под действием внешних сил. Точнее жидкость не имеет собственной формы и приобретает форму сосуда, который она заполняет.

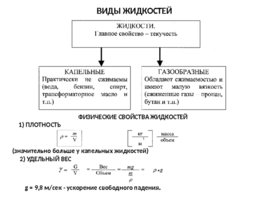
ВИДЫ ЖИДКОСТЕЙ ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ 1) ПЛОТНОСТЬ (значительно больше у капельных жидкостей) 2) УДЕЛЬНЫЙ ВЕС g 9,8 м/сек - ускорение свободного падения.

3) УДЕЛЬНЫЙ ОБЪЕМ - объём , занимаемый единицей массы жидкости При колебаниях С и давления объемы капельных жидкостей изменяются незначительно, поэтому на практике обычно принимают СЖИМАЕМОСТЬ ЖИДКОСТЕЙ Характеризуется коэффициентом сжимаемости - относительное изменение объема жидкости при изменении давления на единицу I / Па - уменьшение объема - увеличение давления ВИДЫ ЖИДКОСТЕЙ - Продолжение

При относительно невысоких давлениях сжимаемостью жидкостей пренебрегают. Вследствие большой сжимаемости газообразных жидкостей их плотность, удельный вес и удельный объем в значительной степени зависят от температуры и давления. Процессы сжатия и расширения газов подчиняются известным из физики законам Бойля-Мариотта и Гей-Люссака для идеальных газов и здесь не рассматриваются. ВИДЫ ЖИДКОСТЕЙ- Продолжение ИСТИННЫЙ МОДУЛЬ СЖАТИЯ Величина, обратная коэффициенту сжимаемости Для газов при постоянной температуре истинный модуль сжатия численно равен давлению .

Вязкость жидкости. Закон Ньютона для вязкой жидкости. Параметры, характеризующие вязкость жидкости. Идеальная жидкость

При движении реальных (вязких) жидкостей в них возникают внутренние напряжения, обусловленные силами внутреннего трения жидкости. Природа этих сил довольно сложна; возникающие в жидкости напряжения связаны с процессом переноса импульса (вектора массовой скорости движения жид-кости). При этом возникающие в жидкости напряжения обусловлены двумя факторами: напряжениями, возни-кающими при деформации сдвига и напряжениями, возникающими при деформации объёмного сжатия.

Наличие сил вязкостного трения в движущейся жидкости подтверждается простым и наглядным опытом. Если в цилиндрическую ёмкость, заполненную жид-костью опустить вращающийся цилиндр, то вскоре придёт в движение (начнёт вращаться вокруг своей оси в том же направлении, что и вращающийся цилиндр) и сама ёмкость с жидкостью. Этот факт свидетельствует о том, что вращательный момент от вращающегося цилиндра был передан через вязкую жидкость самой ёмкости, заполненной жидкостью.

Напряжения, возникающие при деформации сдвига согласно гипотезе Ньютона пропорциональны градиенту скорости в движущихся слоях жидкости, а сила трения между слоями движущейся жидкости будет пропорциональна площади поверхности движущихся слоев жидкости: , где: - сила трения между слоями движущейся жидкости, - площадь поверхности слоев движущейся жидкости, - касательные напряжения, возникающие в жидкости при деформации сдвига, - коэффициент динамической вязкости жидкости.

Величина коэффициента динамической вязкости жид-кости при постоянной температуре и постоянном давлении зависит от внутренних (химических) свойств самой жид-кости. Размерность коэффициента динамической вязкости в системе единиц СИ – Н с/м 2 , в системе СГС – д-с/см . По-следняя размерность носит название пуаза (пз). Таким образом, 1 пз 1 д-с/см , а соотношение между единицами вязкости - 1 да 0,1 Н с/м2.

Помимо коэффициента динамической вязкости жид-кости широко используется коэффициент кинематической вязкости жидкости , представляющий собой отношение коэффициента динамической вязкости к плотности жид-кости: В системе единиц СИ коэффициент кинематической вязкости измеряется в м /с, в системе единиц СГС единицей измерения коэффициента кинематической вязкости жидкости является стоке (cт), т.е. 1 cт 1 см/с.

Коэффициент динамической вязкости чистой воды составляет 1-10 3 н-с/м (или 0,01 пз), коэффициент кинематической вязкости чистой воды составляет МО" м/с (или 0,01 cт). Коэффициенты вязкости жидкостей варьируют- ся в весьма широких пределах от 0,0003 до 0,139 н-с/л 2 . Вязкость жидкости в значительной степени зависит от температуры и давления. При увеличении температуры капельной жидкости коэффициенты её вязкости (как динамический, так и кинематический) резко снижается в десятки и сотни раз, что обусловлено увеличением внутренней энергии молекул жидкости по сравнению с энергией межмолекулярной связи в жидкости.

Зависимость вязкости капельной жидкости от температуры может быть выражена в виде экспоненциальной зависимости : где: - вязкость капельной жидкости при стандартной температуре - 20 С, - экспериментальный температурный коэффициент.

Зависимость вязкости жидкости от давления в широком диапазоне давлений остаётся практически линейной: где: - вязкость жидкости при атмосферном давлении, - экспериментальный коэффициент пропорциональности.

Измерение вязкости жидкостей осуществляется с помощью вискозиметров, работающих на принципе истечения жидкости через малое калиброванное отверстие; вязкость вычисляется по скорости истечения.

Предмет изучения гидростатики. Силы, действующие на жидкость, находящуюся в равновесии. Гидростатическое давление и его свойства. Основное уравнение гидростатики

Предмет изучения гидростатики. Гидростатическое давление и его свойства. Основное уравнение гидростатики Гидростатика - изучат законы равновесия жидкостей и их действие на ограничивающие стенки. Основные понятия гидростатики В гидростатике рассматриваются равновесие жидкости и ее взаимодействие с твердыми телами.

Силы, действующие на жидкость МАССОВЫЕ (ОБЪЕМНЫЕ) СИЛЫ Приложены к частицам жидкости, заполняющим некоторый объем (силы собственной тяжести, инерции и др.) ПОВЕРХНОСТНЫЕ СИЛЫ Действуют лишь на поверхность выделенного объема (атмосферное давление, давление твердого тела на обтекающую его жидкость и др.)

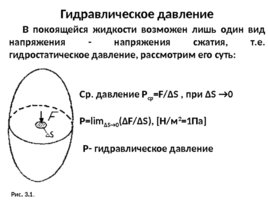
Гидравлическое давление В покоящейся жидкости возможен лишь один вид напряжения - напряжения сжатия, т.е. гидростатическое давление, рассмотрим его суть: Ср. давление Р ср F/ S , при S 0 P lim S 0 ( F/ S), Н/м 2 1Па Р- гидравлическое давление Рис. 3.1 .

Свойства гидравлического давления 1. Всегда направлено по нормали к площадке, на которую действует. 2. Всегда действует одинаково по всем направлениям. 3. Давление в точке зависит от ее координат в пространстве. По мере погружения точки под уровень жидкости давление в ней будет возрастать и наоборот. Газ, находящийся в сосуде, также создает гидростатическое давление на стенки.

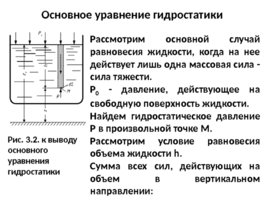
Основное уравнение гидростатики Рассмотрим основной случай равновесия жидкости, когда на нее действует лишь одна массовая сила - сила тяжести. Р 0 - давление, действующее на свободную поверхность жидкости. Найдем гидростатическое давление Р в произвольной точке М. Рассмотрим условие равновесия объема жидкости h. Сумма всех сил, действующих на объем в вертикальном направлении: Рис. 3.2. к выводу основного уравнения гидростатики

Р S - P о S – pgh S 0 - вес столбика жидкости, сократив на S, получим: Р P о pgh. (А) Это основное уравнение гидростатики. Оно позволяет подсчитать давление в любой точке покоящийся жидкости.

Заменив в (А), h Zо –Z, для точки М, получим: Р P0 pg(Z о –Z), откуда, разделив, на pg, получим: Z P/pg Z o P o /pg Z P/pg const Основное уравнение гидростатики Сумма (Z P/pg) называется гидростатическим напором, который, как показано, есть величина постоянная для всего объема неподвижной жидкости.

Измерение гидростатического давления. Жидкостные манометры-пьезометры. Микроманометры

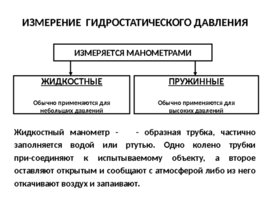
ИЗМЕРЕНИЕ ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ ИЗМЕРЯЕТСЯ МАНОМЕТРАМИ ЖИДКОСТНЫЕ Обычно применяются для небольших давлений ПРУЖИННЫЕ Обычно применяются для высоких давлений Жидкостный манометр - - образная трубка, частично заполняется водой или ртутью. Одно колено трубки при-соединяют к испытываемому объекту, а второе оставляют открытым и сообщают с атмосферой либо из него откачивают воздух и запаивают.

НИВЕЛИРНАЯ И ПЬЕЗОМЕТРИЧЕСКАЯ ВЫСОТЫ

Избыточное или манометрическое давление(при ): (27.3) где ; т.е. глубина погружения h точки жидкости характеризует манометрическое давление в ней. Из (27.3) манометрическое давление равно весу столба жидкости высотой h приходящегося на единицу. НИВЕЛИРНАЯ И ПЬЕЗОМЕТРИЧЕСКАЯ ВЫСОТЫ - Продолжение

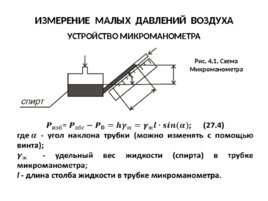
ИЗМЕРЕНИЕ МАЛЫХ ДАВЛЕНИЙ ВОЗДУХА УСТРОЙСТВО МИКРОМАНОМЕТРА Рис. 4.1. Схема Микроманометра

Основные понятия гидродинамики и величины, характеризующие движение жидкости. Задачи гидродинамики

ОСНОВНЫЕ ПОНЯТИЯ ГИДРОДИНАМИКИ Гидродинамика рассматривает законы движения жид-костей. Причинами движения жидкости являются дейст-вующие на нее внешние массовые и поверхностные силы. ОСНОВНЫЕ ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЩИЕ ДВИЖЕНИЕ ЖИДКОСТИ 1. Гидродинамическое давление: 2. Скорость движения:

Эти величины характеризуют неустановившееся дви-жение, так как есть зависимость от времени t , если то это установившееся движение. и , ЗАДАЧИ ГИДРОДИНАМИКИ Определение и , установление связи между ними и законов их изменения при различных случаях движения жидкости. ОСНОВНЫЕ ВЕЛИЧИНЫ, ХАРАКТЕРИЗУЩИЕ ДВИЖЕНИЕ ЖИДКОСТИ - Продолжение

Представление потока жидкости. Элементарная струйка и ее свойства. Величины, применяемые для характеристики элементарной струйки

ПОНЯТИЕ О ПОТОКЕ И ЭЛЕМЕНТАРНОЙ СТРУЙКЕ ЖИДКОСТИ Поток жидкости состоит из совокупности элементарных струек, образующих непрерывную массу частиц, движущихся в каком-либо направлении. Поток ограничен твердыми стенками, а в общем случае и поверхностями соприкосновения жидких и газообразных тел. Основной элемент гидравлической модели потока - ЭЛЕМЕНТАРНАЯ СТРУЙКА. Направление скоростей частиц жидкости в потоке характеризуется линиями тока - воображаемыми кривыми с векторами скоростей частиц, направленными по касательной в соответствующих точках.

ПОНЯТИЕ О ПОТОКЕ И ЭЛЕМЕНТАРНОЙ СТРУЙКЕ ЖИДКОСТИ - Продолжение При установившемся движении линии тока совпадают с траекторией движения частиц потока, таким образом мы получаем трубку тока. ОБЪЁМНЫЙ ПУЧОК ЛИНИЙ ТОКА называется элементарной струйкой . - скорость частиц ds – элементарно малая площадка

СВОЙСТВА ЭЛЕМЕНТАРНОЙ СТРУЙКИ ЖИДКОСТИ ПРИ УСТАНОВИВШЕМСЯ ДВИЖЕНИИ Площадь поперечного сечения струйки и ее форма не зависит от времени (так как формы линий тока не зависят от t). Невозможно перетекание жидкости через боковую поверхность элементарной струйки. Скорость движения жидкости во всех точках поперечного сечения струйки одинакова. По длине потока форма, площадь поперечного сечения элементарной струйки и скорости в поперечных сечениях могут изменяться.

ЖИВОЕ СЕЧЕНИЕ СТРУЙКИ РАСХОД ЭЛЕМЕНТАРНОЙ СТРУЙКИ Элементарно малая площадка ds , перпендикулярная линиям тока. Объем жидкости, проходящей через живое сечение в единицу времени.

Гидравлические параметры жидкости. Коэффициент Кориолиса и его физический смысл. Уравнение неразрывности потока и постоянства расхода при установившемся движении жидкости

ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ПОТОКА В гидравлике различают следующие характери- стики потока: живое сечение , смоченный периметр , гидравлический радиус , расход , средняя скорость . Живым сечением потока называется поверхность (поперечное сечение), нормальная ко всем линиям тока, его пересекающим, и лежащая внутри потока жидкости. Площадь живого сечения обозначается буквой S. Для элементарной струйки жидкости используют понятие живого сечения элементарной струйки (сечение струйки, перпендикулярное линиям тока), площадь которого обозначают через d S.

Смоченный периметр потока – линия, по которой жидкость соприкасается с поверхностями русла в данном живом сечении. Длина этой линии обозначается буквой χ, которая в курсе УМК обозначается (П). В напорных потоках смоченный периметр совпадает с геометрическим периметром, так как поток жидкости соприкасается со всеми твёрдыми стенками. Гидравлическим радиусом R потока называется часто используемая в гидравлике величина, представляющая собой отношение площади живого сечения S к смоченному периметру χ : ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ПОТОКА- продолжение

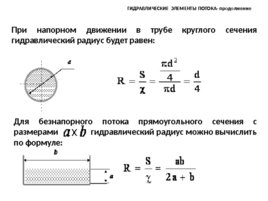
При напорном движении в трубе круглого сечения гидравлический радиус будет равен: Для безнапорного потока прямоугольного сечения с размерами гидравлический радиус можно вычислить по формуле: ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ПОТОКА- продолжение

Расход потока жидкости (расход жидкости) – количество жидкости, протекающей в единицу времени через живое сечение потока. Различают объёмный , массовый и весовой расходы жидкости. Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока. Объёмный расход жидкости измеряется обычно в м 3 /с, дм 3 /с или л/с. Он вычисляется по формуле: где Q - объёмный расход жидкости, V - объём жидкости, протекающий через живое сечение потока, t - время течения жидкости. , ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ПОТОКА- продолжение

Массовый расход жидкости это масса жидкости, протекающей в единицу времени через живое сечение потока. Массовый расход измеряется обычно в кг/с, г/с или т/с и определяется по формуле: где Q м - массовый расход жидкости, M-масса жидкости, протекающий через живое сечение потока, t -время течения жидкости. ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ПОТОКА- продолжение

Весовой расход жидкости это вес жидкости, протекающей в единицу времени через живое сечение потока. Весовой расход измеряется обычно в Н/с, КН/с. Формула для его определения выглядит так: где Q G - весовой расход жидкости, G - вес жидкости, протекающий через живое сечение потока, t – время течения жидкости. Чаще всего используется объёмный расход потока жидкости. С учётом того, что поток складывается из элементарных струек, то и расход потока складывается из расходов элементарных струек жидкости d Q. ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ПОТОКА- продолжение

Расход элементарной струйки – объем жидкости d V, проходящей через живое сечение струйки в единицу времени. Таким образом: если последнее выражение проинтегрировать по площади живого сечения потока можно получить формулу объёмного расхода жидкости, как сумму расходов элементарных струек ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ПОТОКА- продолжение

Применение этой формулы в расчетах весьма затруднительно, так как расходы элементарных струек жидкости в различных точках живого сечения потока различны. Поэтому в практике для определения расхода чаще пользуются понятием средней скорости потока. Средняя скорость потока жидкости Vср в данном сечении это не существующая в действительности скорость потока, одинаковая для всех точек данного живого сечения, с которой должна была бы двигаться жидкость, что бы её расход был равен фактическому. ГИДРАВЛИЧЕСКИЕ ЭЛЕМЕНТЫ ПОТОКА- продолжение

Уравнение Бернулли для идеальной и реальной (вязкой) жидкости (для элементарной струйки и для потока реальной жидкости). Динамическое и статическое давление

Уравнение Бернулли для элементарной струйки идеальной жидкости В потоке идеальной жидкости (ИЖ) потенциальная энергия полностью расходуется на изменение кинетической энергии потока и изменение положения элементов жидкости в поле силы тяжести. Д О П У Щ Е Н И Я: 1. Плавно изменяющееся течение жидкости (установившееся движение, близкое к параллельно-струйному); 2. Жидкость несжимаема. Уравнение Бернулли устанавливает связь между скоростью и давлением в потоке жидкости.

Уравнение Бернулли для элементарной струйки идеальной жидкости - Продолжение Определим удельную механическую энергию такой элементарной струйки d W пот d W пол d W давл . Энергия положения – потенциальная энергия, запасаемая объёмом d V при поднятии его на высоту h: d W пол d Vρgh. Энергия давления – физический смысл ее заключается в том, что под действием гидростатического давления P элементарный объем можно дополнительно поднять на некоторую высоту : h P/ϒ. Уравнение Бернулли представляет собой закон сохранения механической энергии при движении идеальной несжимаемой жидкости

Уравнение Бернулли для элементарной струйки идеальной жидкости - Продолжение Полная удельная энергия, отнесенная к единице массы элементарной струйки e e п e к ϑ 2 /2 P/ρ gh const. Так как для идеальной несжимаемой жидкости. Обладающей абсолютной текучестью, полная удельная энергия не изменится по длине элементарной струйки. Для двух сечений 1 и 2: ϑ 1 2 /2 P 1 /ρ gh 1 ϑ 2 2 /2 P 2 /ρ gh 2. Это уравнение Бернулли для элементарной струйки невязкой жидкости при установившемся движении считается основным уравнением гидродинамики.

Уравнение Бернулли для элементарной струйки реальной (вязкой) жидкости - Продолжение При движении элементарной струйки реальной (вязкой) жидкости вследствие ее вязкости возникает сопротивления движению, а часть энергии потока расходуется на преодоление сопротивления в каналах. Таким образом: ϑ 1 2 /2 P 1 /ρ gh 1 ϑ 2 2 /2 P 2 /ρ gh 2 P w /ρ Это уравнение Бернулли для элементарной струйки реальной жидкости.

Уравнение Бернулли потока реальной жидкости Поток реальной жидкости состоит из множества элементарных струек. Выделим участок потока: S 1 , S 2 – сечения; w 1, w 2 – линейные скорости жидкости; p 1 , p 2 – давления жидкости в сечениях. Местные скорости и кинетическая энергия в различных точках живого сечения различны, поэтому кинетическую энергию для потока движущейся жидкости определяют через среднеквадратичную скорость. (α к1 ) 2 w 1 2 /2 P 1 /ρ gh 1 (α к2 ) 2 w 2 2 /2 P 2 /ρ gh 2 Pw/ρ где: w – средняя скорость, α к – коэффициент Кориолиса

Динамическое и статическое давления При изучении жидкости часто необходимо выразить не изменение абсолютного давления в струе, а лишь изменение давления, связанного с самим движением, т.е. необходимо исключить из рассмотрения действие силы тяжести. Разложим абсолютное давление в точке жидкости: P P P , (1) где P – давление сил тяжести, т.е. давление в состоянии покоя; P – давление, созданное движением. P P 0 ϒh, (2) где P 0 – давление покоя на уровне отсчета. С учетом (1) и (2), подставив их в уравнение Бернулли, получим: (α к2 ) 2 w 1 2 /2 P 1 /ρ (α к2 ) 2 w 2 2 /2 P 2 /ρ Pw/ρ (3)

Динамическое и статическое давления - Продолжение Для газов можно принять: P 0 P ат ; ϒh 0; α к 1; Тогда P P – P ат P изб Умножив все члены уравнения Бернулли (3) на плотность ρ, получим ρ (w 1) 2 /2 P изб const P полн Величина ρ(w 1) 2 /2 – называется динамическим давлением ; Величина P изб P стат – статическое давление . P полн P дин P стат const Это полное давление движущейся жидкости.

Режимы течения жидкостей. Опыты и число Рейнольдса. Критическая скорость потока. Распределение скоростей жидкости в трубопроводах при ламинарном и турбулентном течениях

РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ РЕЖИМЫ ЛАМИНАРНЫЙ Течение без перемешивания частиц и без пульсаций скорости. Линии тока определяются формой канала. ТУРБУЛЕНТНЫЙ Сопровождается интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. Наряду с основным продольным перемещением имеется поперечное и вращательное движение.

Напорным называется поток, у которого по всему периметру живого сечения жидкость соприкасается с твердыми стенками. Примером напорного потока может служить движение вода в водопроводных трубах. Безнапорным называется поток со свободной поверхностью. Примером безнапорного потока является движение воды в реках и каналах. РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ - Продолжение

ОПЫТ РЕЙНОЛЬДСА ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ В ТРУБАХ Предположение о существовании двух режимов движения жидкости было высказано впервые в 1880 году Д. И. Менделеевым. В 1883 году это предположение было подтверждено экспериментально английским ученым Осборном Рейнольдсом. Рис. 1. Схема экспериментальной установки О. Рейнольдса 1, 2 - краны для регулировки скорости движения воды; 3 - трубка для подвода окрашенной жидкости; 4 - стеклянная трубка; 5 - окрашенная жидкость; 6 - мерный сосуд для определения средней скорости жидкости; 7 - сливная трубка.

СРЕДНЯЯ СКОРОСТЬ В ТРУБКЕ ПЛОЩАДЬЮ S где: - объем воды в сосуде 6; - время; - сечение трубки 4. Опыты проводились при постоянном напоре, для поддержания которого использована сливная трубка 7.

ПОЛУЧЕННЫЙ РЕЗУЛЬТАТ При малых скоростях воды краска движется в ней в виде тонкой струйки, не перемешиваясь с водой. При достижении определенной для данных условий опыта движение частиц жидкости приобретает как бы беспорядочный характер, струйка краски начинает размываться, отчего вода окрашивается.

ЧИСЛО РЕЙНОЛЬДСА Рейнольдса показал, что основным критерием для определения режима движения жидкости служит безразмерный параметр (число Рейнольдса). или - средняя линейная скорость жидкости; - диаметр трубы; - кинематическая вязкость жидкости, м 2 /с ; - массовая скорость потока; - динамическая вязкость жидкости; - в общем случае - гидравлический диаметр канала. где:

Число Рейнольдса, при котором ламинарный режим переходит в турбулентный, называют критическим Условие возникновения турбулентного потока при разных диаметрах трубы и разных жидкостях характеризуется одним и тем же , . Число Рейнольдса является критерием подобия и безразмерно : ЧИСЛО РЕЙНОЛЬДСА - Продолжение

КРИТИЧЕСКАЯ СКОРОСТЬ ПОТОКА Скорость , соответствующая критическому числу Рейнольдса, называют критической скоростью: Число Рейнольдса является важной характеристикой течения. Определяет относительную роль сил инерции и сил трения потока. Турбулентное движение в противоположность ламинарному возникает при больших скоростях движения жидкости, наличии больших диаметров труб, малой вязкости жидкости и большей ее плотности.

При больших преобладающее влияние оказывают силы инерции, действие которых приводит к передаче энергии от одного элемента к другому. Ламинарное течение легче осуществить, чем меньше скорость движения Ж, меньше диаметр трубы, больше вязкость жидкости и меньше ее плотность. Турбулентное движение в противоположность ла-минарному возникает при больших скоростях движения жидкости, наличии больших диаметров труб, малой вяз-кости жидкости и большей ее плотности. КРИТИЧЕСКАЯ СКОРОСТЬ ПОТОКА - Продолжение

Гидравлическое сопротивление. Формула Дарси-Вейсбаха. Коэффициент гидравлического трения и его физический смысл. Формула Пуазейля

ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ Возникающие при движении жидкости потери давления можно разбить на две составляющие: , (11.1) где: - потери давления, обусловленные силами трения; - потери давления, обусловленные различными конструктивными элементами и местными преградами в потоке (поворот потока, сужение, расширение, задвижка и т. п.).

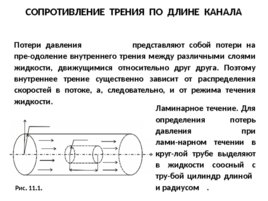
СОПРОТИВЛЕНИЕ ТРЕНИЯ ПО ДЛИНЕ КАНАЛА Потери давления представляют собой потери на пре-одоление внутреннего трения между различными слоями жидкости, движущимися относительно друг друга. Поэтому внутреннее трение существенно зависит от распределения скоростей в потоке, а, следовательно, и от режима течения жидкости. Ламинарное течение. Для определения потерь давления при лами-нарном течении в круг-лой трубе выделяют в жидкости соосный с тру-бой цилиндр длиной и радиусом . Рис. 11.1.

С внешней стороны на поверхность цилиндра дейст-вует напряжение внутреннего трения: . (11.2) Формула (11.2) - Закон Ньютона для вязкой жидкости, где - динамический коэффициент вязкости. Следовательно, на всю поверхность цилиндра действует сила: , (11.3) СОПРОТИВЛЕНИЕ ТРЕНИЯ ПО ДЛИНЕ КАНАЛА - Продолжение которая определяет сопротивление трения по длине канала.

ФОРМУЛА ДАРСИ-ВЕЙСБАХА. КОЭФФИЦИЕНТ ГИДРАВЛИЧЕСКОГО ТРЕНИЯ Потери напора по длине трубопровода можно опреде-лить по формуле Дарси-Вейсбаха: , где: - относительная длина трубы; - коэффициент гидравлического трения (коэффициент Дарси); - длина трубопровода; - диаметр трубопровода.

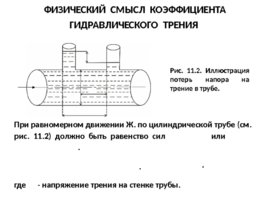
ФИЗИЧЕСКИЙ СМЫСЛ КОЭФФИЦИЕНТА ГИДРАВЛИЧЕСКОГО ТРЕНИЯ Рис. 11.2. Иллюстрация потерь напора на трение в трубе. При равномерном движении Ж. по цилиндрической трубе (см. рис. 11.2) должно быть равенство сил или где - напряжение трения на стенке трубы. , . .

Поэтому . Решив совместно (34.4) и (34.5), получим: . Таким образом, коэффициент есть величина, пропор-циональная отношению напряжения трения на стенке трубы к динамическому давлению, подсчитанному по средней ско-рости. При ламинарном течении в круглой трубе коэффициент гидравлического трения определяется по формуле Пуазейля ФИЗИЧЕСКИЙ СМЫСЛ КОЭФФИЦИЕНТА ГИДРАВЛИЧЕСКОГО ТРЕНИЯ – Продолжение. .

КОЭФФИЦИЕНТ ГИДРАВЛИЧЕСКОГО ТРЕНИЯ. ФОРМУЛА ПУАЗЕЙЛЯ Поскольку течение стационарно, это сила уравновешивается разностью сил давлений и на торцах цилиндра. Таким образом: , откуда: . Учитывая граничное условие при , где - радиус трубы, проинтегрируем правую часть уравнения от до , а левую соответственно от 0 до : .

Таким образом, при ламинарном течении вязкой жид-кости по сечению круглого трубопровода скорости распре-делены по закону параболы. При максимальная скорость в центре трубы . Расход жидкости равен объему параболоида, т. е.: . Определим среднюю скорость: , откуда потери давления: . КОЭФФИЦИЕНТ ГИДРАВЛИЧЕСКОГО ТРЕНИЯ. ФОРМУЛА ПУАЗЕЙЛЯ - Продолжение

Отметим, что это один из немногих случаев, когда интегрирование уравнения движения вязкой жидкости возможно. Преобразуем полученную формулу: , где - коэффициент гидравлического трения. КОЭФФИЦИЕНТ ГИДРАВЛИЧЕСКОГО ТРЕНИЯ. ФОРМУЛА ПУАЗЕЙЛЯ - Продолжение

Сопротивление трения по длине канала при турбулентном течении. Исследование Никурадзе и их результаты. Зависимость коэффициента гидравлического трения от числа Рейнольдса

СОПРОТИВЛЕНИЕ ТРЕНИЯ ПО ДЛИНЕ КАНАЛА ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ При турбулентном движении (течении) коэффициент трения , а его зависимость от числа Рейнольдса определяется степенью шероховатости труб. Эту зависимость исследовали экспериментально на трубах с искусственной равномерной шероховатостью.

В качестве параметра использовалась относительная шероховатость: - средняя величина шероховатости; - радиус трубы. где: Результаты исследований, например ученого Никурадзе, можно свести в таблицу. СОПРОТИВЛЕНИЕ ТРЕНИЯ ПО ДЛИНЕ КАНАЛА ПРИ ТУРБУЛЕНТНОМ ТЕЧЕНИИ - - Продолжение ,

ЗАВИСИМОСТЬ КОЭФФИЦИЕНТА ГИДРАВЛИЧЕСКОГО ТРЕНИЯ ОТ ЧИСЛА РЕЙНОЛЬДСА. ИССЛЕДОВАНИЯ НИКУРАДЗЕ Турбулентное течение . Распределение скоростей в турбулентном потоке не имеет параболического характера (рис. 1.12), а коэффициент трения λ 64/Re, его зависимость от числа Рейнольдса определяются степенью шероховатости стенок труб. Эту зависимость экспериментально исследовал Никурадзе на трубах с искусственной равномерной шероховатостью. На рис. 2.1 представлено шесть кривых, полученных для труб с различной относительной шероховатостью δ Δ/r, где Δ — средняя высота шероховатости, а r — радиус трубы. Кривые 1 ...6 соответствуют относительной шероховатости δ 0,066; 0,032; 0,067; 0,007; 0,004; 0,002.

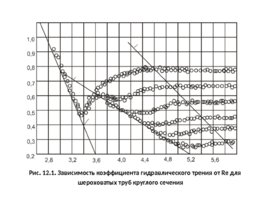
Рис. 12.1. Зависимость коэффициента гидравлического трения от Re для шероховатых труб круглого сечения

АНАЛИЗ КРИВЫХ НИКУРАДЗЕ Анализируя кривые Никурадзе, можно прийти к выводу, что этот график распадается на пять зон. Зона 1 - область ламинарного течения. Кривые для труб разной шероховатости в этой зоне совпадают с прямой а , описываемой уравнением: Зона 2 - область перехода из ламинарного режима в турбулентный. Для этой зоны справедливо уравнение, полученное Н. В. Френкелем: .

Зона 3 - турбулентный режим течения, область гидравлически гладких труб , где зависит только от числа Рейнольдса и не зависит, от шероховатости (прямая б ). Для этой зоны справедлива формула Блазиуса: Зона 4 - турбулентный режим течения , переходная область (между областями гидравлически гладких труб и квадратичной) между прямыми б и в (рис. 12.1), где за-висит как от шероховатости, так и от числа Рейнольдса. Для переходной области справедлива формула А. Д. Альтшуля: АНАЛИЗ КРИВЫХ НИКУРАДЗЕ - Продолжение . .

Зона 5 - турбулентный режим течения , квадратичная зона сопротивления (правее прямой в), где практически не зависит от числа Рейнольдса и является функцией только относительно шероховатости. Для этой зоны применяют формулу Никурадзе: Результаты исследований Никурадзе представлены в таблице, составленной автором настоящего УМК ТИГР. Данная таблица удобна для расчетов в рамках дипломного и курсового проектирования. АНАЛИЗ КРИВЫХ НИКУРАДЗЕ - Продолжение .

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ГИДРАВЛИЧЕСКОГО ТРЕНИЯ ДЛЯ РАЗЛИЧНЫХ ВИДОВ ТЕЧЕНИЙ ЖИДКОСТИ И РАЗНЫХ ШЕРОХОВАТОСТЕЙ КАНАЛА Режим течения жидкости соответствующий номеру зоны на зависимостях : 1 - Ламинарное течение. 2 - Переход из ламинарного режима в турбулентный. 3 - Турбулентный режим течения в области «гидравличес- ких гладких труб». 4 - Турбулентный режим течения (переходная зона между областями гидравлических гладких труб и квадратичной зоной сопротивления). 5 - Турбулентный режим течения, квадратичная зона со-противления.

Номер зоны на зависимостях Пределы изменения (lg Re) Пределы изменения относительной шероховатости и ее влияние на λ Пределы изменения λ (lg 100 λ) Формула для определения коэффициента гидравлического трения и имя ее автора 1 0,002-0,006 0,2-1,1 Формула Пуазейля 2 0,002-0,066 Уравнение Френкеля 3 0,002-0,066 Не влияет на λ λ зависит только от Re; не зависит от δ Формула Блазиуса 4 0,002-0,006 Формула Альтшуля 5 0,002-0,066 На λ влияет только δ, и практически не влияет Re Формула Никуридзе ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ГИДРАВЛИЧЕСКОГО ТРЕНИЯ ДЛЯ РАЗЛИЧНЫХ ВИДОВ ТЕЧЕНИЙ ЖИДКОСТИ И РАЗНЫХ ШЕРОХОВАТОСТЕЙ КАНАЛА - Продолжение Таблица для определения коэффициентов гидравлического трения для различных видов течения жидкости и разных шероховатостей канала

Основные виды местных гидравлических сопротивлений и формулы их расчета

ОСНОВНЫЕ ВИДЫ МЕСТНЫХ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ И ФОРМУЛЫ ДЛЯ ИХ РАСЧЕТА КОЭФФИЦИЕНТ СОПРОТИВЛЕНИЯ ГИДРАВЛИЧЕСКОГО ТРЕНИЯ Потери давления на преодоление внутреннего трения: , , (13.1) где - коэффициент сопротивления гидравлического трения.

МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ Потери давления представляют собой затраты энергии на внутреннее трение при преодолении различных пре-пятствий в трубопроводах - вентилей, колен, диффузоров, сужения и расширения и др., которые называют местными гидравлическими сопротивлениями. Потери давления на этих сопротивлениях зависят от квадрата средней скорости потока до (или после) препятствия, их определяют по формуле Вейсбаха: где: - средняя скорость потока до местного гидравлического сопротивления; - коэффициент местного гидравлического сопротив-ления.

Обычно коэффициент местного гидравлического со-противления определяют экспериментальным путем и выражают в виде эмпирических формул, графиков или таблиц. Рассмотрим некоторые виды местных сопротивлений При расчете трубопроводов наряду с гидравлическим сопротивлением внутренних стенок следует учитывать МЕСТНЫЕ СОПРОТИВЛЕНИЯ, в которых вследствие изменения размеров или конфигурации русла происходят изменения скорости потока, отрыв транзитной струи от стенок русла и возникновение вихреобразования. МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ - Продолжение

Простейшие местные гидравлические сопротивления можно разбить на: 1. диффузор (постепенное расширение канала). 2. конфузор (постепенное сужение канала). 3. внезапное расширение канала; 4. внезапное сужение канала; 5. поворот русла. Более сложные случаи местных сопротивлений пред-ставляют собой соединения или комбинации перечислен-ных простейших сопротивлений. МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ - Продолжение

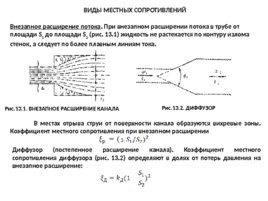
ВИДЫ МЕСТНЫХ СОПРОТИВЛЕНИЙ Внезапное расширение потока . При внезапном расширении потока в трубе от площади S 1 до площади S 2 (рис. 13.1) жидкость не растекается по контуру излома стенок, а следует по более плавным линиям тока. В местах отрыва струи от поверхности канала образуются вихревые зоны. Коэффициент местного сопротивления при внезапном расширении Диффузор (постепенное расширение канала). Коэффициент местного сопротивления диффузора (рис. 13.2) определяют в долях от потерь давления на внезапное расширение: Рис.13.1. ВНЕЗАПНОЕ РАСШИРЕНИЕ КАНАЛА Рис.13.2. ДИФФУЗОР 1-

где к д - коэффициент, учитывающий уменьшение потерь давления в диффузоре по сравнению с потерями давления при внезапном расширении с тем же соотношением сечения соединяемых труб. Коэффициент к д зависит от угла конусности 0 Ь Для 0 4; 8; 12 соответственно к д 0,12; 0,14; 0,23. При 0! д sin Oi, а при 01 5О к д принимают равным 1. Внезапное сужение потока. При внезапном сужении потока (рис. 13.3) также образуются вихревые зоны, и происходит сжатие потока. Коэффициент местного сопротивления при внезапном сужении Вход в канал. Потери напора при входе в канал зависят от условий входа. Условия входа в канал с острыми кромками наиболее затруднены. Коэффициент местного сопротивления такого участка (рис. 13.4, а) зависит от толщины δ , диаметра d и длины Ь выступающей части трубы, и его можно определить по графикам рис. 13.4, б. Рис.13.3. СХЕМА ТОКА ПРИ ВНЕЗАПНОМ РАСШИРЕНИЕ КАНАЛА

При входе в канал с толстыми стенками, например в стене (рис. 13.6), коэффициент местного сопротивления получают из (2.18), приняв S 1 со, ξ вх 0,5. При плавном входе в канал коэффициент местного сопротивления зависит от радиуса закругления (рис. 13.5). ВИДЫ МЕСТНЫХ СОПРОТИВЛЕНИЙ - Продолжение Рис.13.4. ВХОД В КАНАЛ С ОСТРЫМИ КРОМКАМИ (а), ЗАВИСИМОСТЬ Рис.13.5. ПЛАВНЫЙ ВХОД В КАНАЛ: БЕЗ ТОРЦЕСТЕНКИ(а), С ТОРЦЕВОЙ СТЕНКИ (б) ЗАВИСИМОСТЬ Рис.13.6. ВХОД В КАНАЛ С ТОЛСТЫМИ СТЕНКАМИ

Конфузор (постепенное сужение канала) Коэффициент местного сопротивления при постепенном сужении (рис. 13.7, а ) определяется в долях от потерь напора при внезапном сужении, как и при определении коэффициента потерь диффузора: где - коэффициент, учитывающий уменьшение потерь напора в конфузоре по сравнению с потерями напора при внезапном сужении; коэффициент зависит от угла схо-димости конфузора определяется по графику (рис. 13.7, б .) ВИДЫ МЕСТНЫХ СОПРОТИВЛЕНИЙ - Продолжение

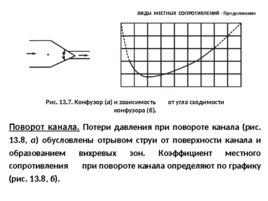
Рис. 13.7. Конфузор ( а ) и зависимость от угла сходимости конфузора ( б ). Поворот канала. Потери давления при повороте канала (рис. 13.8, а ) обусловлены отрывом струи от поверхности канала и образованием вихревых зон. Коэффициент местного сопротивления при повороте канала определяют по графику (рис. 13.8, б ). ВИДЫ МЕСТНЫХ СОПРОТИВЛЕНИЙ - Продолжение

Выход в открытый канал. Коэффициент местного со-противления для данного случал можно получить из (13.3), приняв , . Значения коэффициентов для других местных со-противлений можно найти в справочниках и специальной литературе. Рис. 13.8. Поворот канала ( а ) и график зависимости от угла (б). ВИДЫ МЕСТНЫХ СОПРОТИВЛЕНИЙ - Продолжение

Результирующее гидравлическое сопротивление (на примере электрической машины). Составление эквивалентной гидравлической схемы (ЭГС). Электрогидравлическая аналогия

Результирующее гидравлическое сопротивление (на примере электрической машины) В электрических машинах при движении охлаждающих сред проявляются все виды рассмотренных выше гидравлических сопротивлении. Поэтому пути движения охлаждающих сред могут быть достаточно сложными. Расчет суммарного гидравлического сопротивления электрической машины - одна из важнейших задач ее вентиляционного (гидравлического) расчета.

Составление эквивалентной гидравлической схемы (ЭГС) электрической машины Двигаясь в канале, струя жидкости или газа преодолевает гидравлические сопротивления различного вида. Эти сопротивления можно считать соединенными последовательно или параллельно. По аналогии с электрической цепью аэродинамические и гидравлические тракты принято изображать в виде сопротивлений, соединенных между собой отрезками каналов, не имеющих сопротивления.

Рассмотрим порядок составления эквивалентной гидравлической схемы (ЭГС) на примере небольшой машины постоянного тока без аксиальных каналов в якоре (рис. 15.1, а). Поток воздуха, характеризующийся расходом Q, встречает на своем пути последовательно различные гидравлические сопротивления. Чтобы установить причину этих сопротивлений, начинающему расчетчику рекомендуется выполнить упрощенное изображение вентиляционного тракта (рис. 15.1, б). По аналогии с электрической цепью вентиляционный тракт можно представить в виде ЭГС (рис. 15.1, в).

Из рисунка (15.1. б) видно, что сечение канала в общем случае переменно. Поэтому при заданном значении расхода Q скорость среды оказывается также переменной. Потери давления на преодоление какого-либо гидравлического сопротивления вычисляют с помощью коэффициента гидравлического сопротивления - как долю динамического давления Ap z ξp/(2w 2 ).

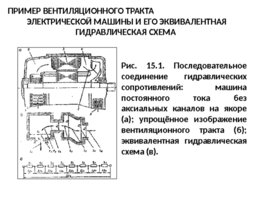
ПРИМЕР ВЕНТИЛЯЦИОННОГО ТРАКТА ЭЛЕКТРИЧЕСКОЙ МАШИНЫ И ЕГО ЭКВИВАЛЕНТНАЯ ГИДРАВЛИЧЕСКАЯ СХЕМА Рис. 15.1. Последовательное соединение гидравлических сопротивлений: машина постоянного тока без аксиальных каналов на якоре (а); упрощённое изображение вентиляционного тракта (б); эквивалентная гидравлическая схема (в).

Закон Адкинсона. Электрогидравлическая аналогия

ЗАКОН АДКИНСОНА. ЭЛЕКТРОГИДРАВЛИЧЕСКАЯ АНАЛОГИЯ Чтобы исключить из расчета переменную скорость движения, потери давления можно выразить как функцию неизменной для данного канала величины расхода Q : ; (39.1) где - гидравлическое сопротивление, соответствующее коэффициенту местного сопротивленияучастка: ; (39.2) Размерность гидравлического сопротивления можно определить из: ;

Выражение (39.1) называют законом Адкинсона. Он устанавливает связь между падением давления на гидравлическом сопротивлении z и расходом Q в ЭГС, аналогично тому, как закон Ома в электрической цепи устанавливает связь между падением напряженияна сопротивлении R и током I . На этом основании говорят об электрогидравлической аналогии:- закон Адкинсона;- закон Ома. ЗАКОН АДКИНСОНА. ЭЛЕКТРОГИДРАВЛИЧЕСКАЯ АНАЛОГИЯ - Продолжение

Однако эта аналогия будет неполной, так как гидравлическое сопротивление z зависит не только от свойств, но и от расхода охлаждающей среды, т.е. электрическое сопротивление R аналогично z Q . Следовательно, ЭГС можно рассматривать как нелинейную электрическую цепь и применять для ее расчета методы, разработанные для электрических цепей, в частности законы Кирхгофа. Рассмотрим, как можно использовать эти законы для преобразования и упрощения ЭГС. ЗАКОН АДКИНСОНА. ЭЛЕКТРОГИДРАВЛИЧЕСКАЯ АНАЛОГИЯ - Продолжение

Определение суммарного сопротивления эквивалентной гидравлической схемы (ЭГС)

ОПРЕДЕЛЕНИЕ СУММАРНОГО СОПРОТИВЛЕНИЯ ЭГС Последовательное соединение сопротивлений. При после-довательном соединении гидравлических сопротивлений суммарный перепад давления: где - суммарное гидравлическое сопротивление всей схемы. Потери давления на каждом участке: С другой стороны: где - число последовательно соединенных участков. , (17.1) . (17.2) , (17.3)

Приравнивая (17.1) и (17.3), и сокращая полученное равенство на , запишем: , (17.4) Таким образом, при последовательном соединении гидравлических сопротивлении суммарное сопротивление ЭГС определяется, как для электрической цепи. Параллельное соединение сопротивлений. При парал-лельном соединении гидравлических сопротивлений (рис. 1.1) ввиду нелинейности закона Адкинсона расчет сум-марного сопротивления усложняется. ОПРЕДЕЛЕНИЕ СУММАРНОГО СОПРОТИВЛЕНИЯ ЭГС - Продолжение

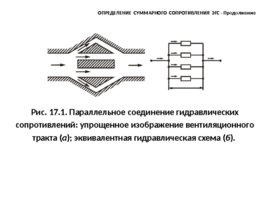
Рис. 17.1. Параллельное соединение гидравлических сопротивлений: упрощенное изображение вентиляционного тракта ( а ); эквивалентная гидравлическая схема ( б ). ОПРЕДЕЛЕНИЕ СУММАРНОГО СОПРОТИВЛЕНИЯ ЭГС - Продолжение

Из уравнения неразрывности потока для рассматривае-мого вентиляционного тракта следует, что расход охлаж-дающей среды в любом сечении вентиляционного тракта должен оставаться постоянным, т.е. где - число параллельно включенных участков. , (1.5) ОПРЕДЕЛЕНИЕ СУММАРНОГО СОПРОТИВЛЕНИЯ ЭГС - Продолжение Полученное выражение аналогично первому закону Кирхгофа для электрической цепи.

Так как давления до разветвления и после него могут иметь только одно значение, разность давлений на участках - постоянная величина, т.е.: , (17.6) Перепад давления на i-м участке , откуда: , (17.7) Тогда, в соответствии с (17.5): , (17.8) ОПРЕДЕЛЕНИЕ СУММАРНОГО СОПРОТИВЛЕНИЯ ЭГС - Продолжение

В то же время для всей цепи , откуда , (17.9) Приравниваем (17.8) и (17.9): тогда результирующее гидравлическое сопротивление параллельно включенных : (17.10) ОПРЕДЕЛЕНИЕ СУММАРНОГО СОПРОТИВЛЕНИЯ ЭГС - Продолжение

Эта формула не имеет аналогов в расчетах линейных электрических цепей, для которых Таким образом, для ЭГС следует, что для двух параллельно соединенных элементов суммарное гидравлическое сопротивление: (17.11) , т.е. выражение получается более сложным, чем для элек-трической цепи. ОПРЕДЕЛЕНИЕ СУММАРНОГО СОПРОТИВЛЕНИЯ ЭГС - Продолжение

Преобразование сложных эквивалентных гидравлических схем

ПРЕОБРАЗОВАНИЕ СЛОЖНЫХ ЭГС При последовательном соединении гидравлических сопротивлений (см. рис. 38.1, в ) участок вентиляционного тракта называют простым трактом, при параллельном соединении (рис. 40.1. б ) - разветвленным. Для сложных ЭГС, типичных для электрических машин, расчет суммарных гидравлических сопротивлений усложняется. Суммарное сопротивление сложной ЭГС определяют следующим образом.

ПРЕОБРАЗОВАНИЕ СЛОЖНЫХ ЭГС - Продолжение В сложной ЭГС выделяют простые тракты и определяют их эквивалентное гидравлическое сопротивление по (40.3). Затем выделяют разветвленные тракты и определяют их эквивалентное гидравлическое сопротивление по (40.8). Вновь находят простые тракты и определяют их суммарное гидравлическое сопротивление и т.д. В итоге получают суммарное гидравлическое сопротивление z c всей гидравлической или вентиляционной системы.

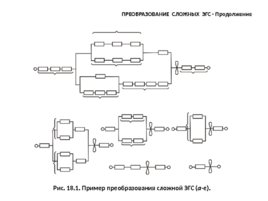
ПРЕОБРАЗОВАНИЕ СЛОЖНЫХ ЭГС - Продолжение Рис. 18.1. Пример преобразования сложной ЭГС ( а - е ).

ТИПЫ СХЕМ ВЕНТИЛЯЦИИ И ИХ ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ Как видно из приведенных примеров, существует много конструкций схем вентиляции электрических машин, однако, все их многообразие можно свести к нескольким характерным типам ЭГС. В табл. приведены наиболее часто встречающиеся схемы вентиляции различных электрических машин и их ЭГС.

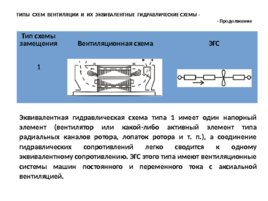
ТИПЫ СХЕМ ВЕНТИЛЯЦИИ И ИХ ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ - - Продолжение Тип схемы замещения Вентиляционная схема ЭГС 1 Эквивалентная гидравлическая схема типа 1 имеет один напорный элемент (вентилятор или какой-либо активный элемент типа радиальных каналов ротора, лопаток ротора и т. п.), а соединение гидравлических сопротивлений легко сводится к одному эквивалентному сопротивлению. ЭГС этого типа имеют вентиляционные системы машин постоянного и переменного тока с аксиальной вентиляцией.

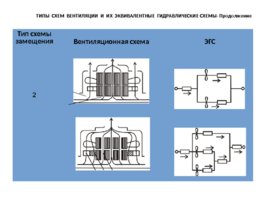
ТИПЫ СХЕМ ВЕНТИЛЯЦИИ И ИХ ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ- Продолжение Тип схемы замещения Вентиляционная схема ЭГС 2

ТИПЫ СХЕМ ВЕНТИЛЯЦИИ И ИХ ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ - Продолжение Эквивалентная гидравлическая схема типа 2 содержит два (или более) вентилятора или других напорных элементов, включенных параллельно и имеющих общее эквивалентное гидравлическое сопротивление входа z BX . Выход из камер горячего воздуха (пространство между сердечником статора и станиной) и камер лобовых частей может быть раздельным (схема 2, а ) или общим (схема 2, б ). К этому типу относятся ЭГС вентиляционных систем асинхронных машин с радиальной схемой вентиляции, у которых напорными элементами служат радиальные каналы ротора (р 1 ), прямолинейные участки лобовых частей (р 2 ) и головки лобовых частей обмотки ротора с напаянными лопатками (р 3 ).

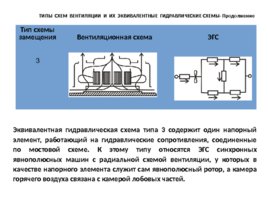
ТИПЫ СХЕМ ВЕНТИЛЯЦИИ И ИХ ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ- Продолжение Тип схемы замещения Вентиляционная схема ЭГС 3 Эквивалентная гидравлическая схема типа 3 содержит один напорный элемент, работающий на гидравлические сопротивления, соединенные по мостовой схеме. К этому типу относятся ЭГС синхронных явнополюсных машин с радиальной схемой вентиляции, у которых в качестве напорного элемента служит сам явнополюсный ротор, а камера горячего воздуха связана с камерой лобовых частей.

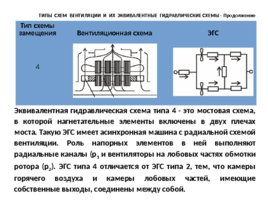
Тип схемы замещения Вентиляционная схема ЭГС 4 Эквивалентная гидравлическая схема типа 4 - это мостовая схема, в которой нагнетательные элементы включены в двух плечах моста. Такую ЭГС имеет асинхронная машина с радиальной схемой вентиляции. Роль напорных элементов в ней выполняют радиальные каналы (р 1 и вентиляторы на лобовых частях обмотки ротора (р 2 ). ЭГС типа 4 отличается от ЭГС типа 2, тем, что камеры горячего воздуха и камеры лобовых частей, имеющие собственные выходы, соединены между собой. ТИПЫ СХЕМ ВЕНТИЛЯЦИИ И ИХ ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ - Продолжение

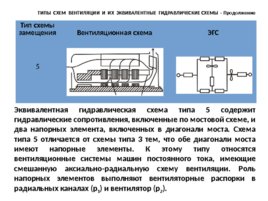
Тип схемы замещения Вентиляционная схема ЭГС 5 Эквивалентная гидравлическая схема типа 5 содержит гидравлические сопротивления, включенные по мостовой схеме, и два напорных элемента, включенных в диагонали моста. Схема типа 5 отличается от схемы типа 3 тем, что обе диагонали моста имеют напорные элементы. К этому типу относятся вентиляционные системы машин постоянного тока, имеющие смешанную аксиально-радиальную схему вентиляции. Роль напорных элементов выполняют вентиляторные распорки в радиальных каналах (p 1 ) и вентилятор (р 2 ). ТИПЫ СХЕМ ВЕНТИЛЯЦИИ И ИХ ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ - Продолжение

Все приведенные схемы вентиляции относятся к самовентилируемым электрическим машинам. Машины, работающие с независимой вентиляцией при разомкнутом цикле, могут иметь любую из приведенных схем с добавлением еще одного напорного элемента - внешнего вентилятора. Таким образом, можно получить еще ряд схем, имеющих последовательное или смешанное соединение элементов. В качестве примера можно привести ЭГС асинхронной машины, имеющей схему типа 4 и работающей с независимой вентиляцией по разомкнутому циклу. ТИПЫ СХЕМ ВЕНТИЛЯЦИИ И ИХ ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ - Продолжение

Приведенные типы ЭГС не охватывают всего многообразия существующих вентиляционных систем электрических машин. Однако большинство ЭГС после упрощения можно, свести к одному из указанных типов. ТИПЫ СХЕМ ВЕНТИЛЯЦИИ И ИХ ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ- Продолжение

Вопрос 2.19. Вентиляционные системы электрических машин различных типов

ВЕНТИЛЯЦИОННЫЕ СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ МАШИН РАЗЛИЧНЫХ ТИПОВ Рассмотрим примеры составления эквивалентной гидравлической схемы (ЭГС) конкретных типов электрических машин (ЭМ). Асинхронные двигатели. Наибольшее распространение получил асинхронный двигатель со степенью защиты IP44 (рис. 19.1), имеющий наружную и внутреннюю вентиляционные системы. Наружная система вентиляции аксиальная, разомкнутая.

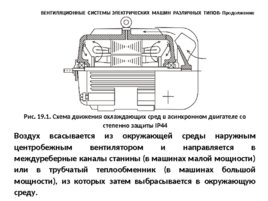
Рис. 19.1. Схема движения охлаждающих сред в асинхронном двигателе со степенно защиты IP44 Воздух всасывается из окружающей среды наружным центробежным вентилятором и направляется в междуреберные каналы станины (в машинах малой мощности) или в трубчатый теплообменник (в машинах большой мощности), из которых затем выбрасывается в окружающую среду. ВЕНТИЛЯЦИОННЫЕ СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ МАШИН РАЗЛИЧНЫХ ТИПОВ- Продолжение

ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ НАРУЖНОЙ И ВНУТРЕННЕЙ СИСТЕМ ВЕНТИЛЯЦИИ ЭМ ЭГС наружной системы вентиляции (рис. 19.2) относится к первому типу и представляет собой последовательное соединение гидравлических сопротивлений: z BX - входа через решетку кожуха; z K - внезапного расширения под кожухом; z П - поворота при выходе из вентилятора; z МР - внезапного сужения при входе в междуреберное пространство; z Bb IX - выхода. рис. 19.2

Для определения названных сопротивлений находят площади сечений соответствующих участков вентиляционного тракта, а затем коэффициенты гидравлических сопротивлений. Эквивалентная гидравлическая схема внутренней системы вентиляции. В машинах малой мощности внутренняя система вентиляции (рис. 19.1) радиальная, замкнутая. В качестве вентилятора используют крылышки на короткозамыкающих кольцах ротора. Воздух, выходящий из вентилятора, разветвляется на два потока - один обтекает лобовые части, другой проходит через «решетку» лобовых частей. ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ НАРУЖНОЙ И ВНУТРЕННЕЙ СИСТЕМ ВЕНТИЛЯЦИИ ЭМ - Продолжение

Эти потоки соединяются и обтекают поверхности станины и подшипниковых щитов, выполняющие в данном случае роль теплообменника, затем охлажденный воздух подается к рабочему колесу вентилятора. Для упорядочения движения внутреннего воздуха в асинхронных двигателях с высотами оси вращения выше 160мм устанавливаются специальные перегородки в виде диффузоров. Эквивалентная гидравлическая схема внутренней системы вентиляции асинхронного двигателя (см. рис. 42.1) изображена на рис. 42.3. ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ НАРУЖНОЙ И ВНУТРЕННЕЙ СИСТЕМ ВЕНТИЛЯЦИИ ЭМ - Продолжение

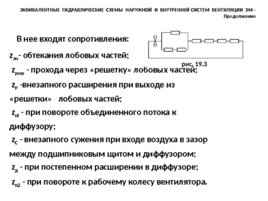
z лч - обтекания лобовых частей; z реш - прохода через «решетку» лобовых частей; z P -внезапного расширения при выходе из «решетки» лобовых частей; z пl - при повороте объединенного потока к диффузору; z С - внезапного сужения при входе воздуха в зазор между подшипниковым щитом и диффузором; z д - при постепенном расширении в диффузоре; z п2 - при повороте к рабочему колесу вентилятора. ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ НАРУЖНОЙ И ВНУТРЕННЕЙ СИСТЕМ ВЕНТИЛЯЦИИ ЭМ - Продолжение рис. 19.3 В нее входят сопротивления:

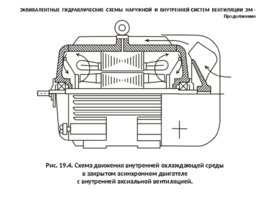
Рис. 19.4. Схема движения внутренней охлаждающей среды в закрытом асинхронном двигателе с внутренней аксиальной вентиляцией. ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ НАРУЖНОЙ И ВНУТРЕННЕЙ СИСТЕМ ВЕНТИЛЯЦИИ ЭМ - Продолжение

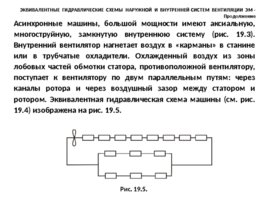
Асинхронные машины, большой мощности имеют аксиальную, многоструйную, замкнутую внутреннюю систему (рис. 19.3). Внутренний вентилятор нагнетает воздух в «карманы» в станине или в трубчатые охладители. Охлажденный воздух из зоны лобовых частей обмотки статора, противоположной вентилятору, поступает к вентилятору по двум параллельным путям: через каналы ротора и через воздушный зазор между статором и ротором. Эквивалентная гидравлическая схема машины (см. рис. 19.4) изображена на рис. 19.5. Рис. 19.5. ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ НАРУЖНОЙ И ВНУТРЕННЕЙ СИСТЕМ ВЕНТИЛЯЦИИ ЭМ - Продолжение

Ветвь каналов статора содержит следующие гидравлические сопротивления: z cc - внезапного сужения перед входом в «карманы»; z пс1 - поворота в «карманы»; z ск - внезапного сужения в «карманах»; z тск - трения в карманах; z пк2 - поворота при выходе из карманов; z рл , - внезапного расширения в зоне лобовых частей обмотки статора; z лч - обтекания лобовых частей; z рс - внезапного расширения при подходе воздуха к торцам ротора. ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ НАРУЖНОЙ И ВНУТРЕННЕЙ СИСТЕМ ВЕНТИЛЯЦИИ ЭМ - Продолжение Ветвь зазора и каналов ротора состоит из сопротивлений: сужения z СЗ , трения z T3 , расширения z P3 .

Асинхронные двигатели со степенью защиты IP23 имеют радиальную систему вентиляции (рис. 19.5). В качестве венти-лятора в них служат лопатки ротора. Воздух поступает в двигатель через окна в подшипниковых щитах, проходит через вентилятор, омывает лобовые части обмотки статора, поступает в канал между сердечником статора и станиной и выбрасывается через отверстия в станине. Рис. 19.6. Схема движения охлаждающей среды в асинхронном двигателе со степенью защиты IP23 с радиальной системой вентиляции ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ НАРУЖНОЙ И ВНУТРЕННЕЙ СИСТЕМ ВЕНТИЛЯЦИИ ЭМ - Продолжение

Эквивалентная гидравлическая схема машины, представленной на рис. 19.6, изображена на рис. 19.1. Входной участок ЭГС состоит из сопротивлений: z вх - входа; z p.вх -внезапного расширения; z п.вх - поворота струи в аксиальном направлении. Рис. 19.7. Схема движения охлаждающей среды в двигателе постоянного тока со степенью защиты IP23 с аксиальной вентиляцией ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ НАРУЖНОЙ И ВНУТРЕННЕЙ СИСТЕМ ВЕНТИЛЯЦИИ ЭМ - Продолжение

Эквивалентная гидравлическая схема защищенных двигателей с радиальной вентиляцией представляет собой простой разомкнутый тракт, состоящий из следующих гидравлических сопротивлений: z BX - входа через окно в подшипниковом щите; z p - внезапного расширения; z Д –диффузора; z п1 - поворота к лопаткам ротора; z лч - обтекания лобовых частей; z cc - внезапного сужения при входе в канал между статором и станиной; z пк – поворота в этом канале; z c.вых -внезапного сужения при выходе из машины; z вых - выхода из машины. ЭКВИВАЛЕНТНЫЕ ГИДРАВЛИЧЕСКИЕ СХЕМЫ НАРУЖНОЙ И ВНУТРЕННЕЙ СИСТЕМ ВЕНТИЛЯЦИИ ЭМ - Продолжение

Вопрос 2.20. Устройств и принцип действия вентиляторов электрических машин. Диаграммы скоростей частиц воздуха вентиляторов с различной конструкцией лопаток (центробежный и осевой вентиляторы). Особенности конструкций встроенных вентиляторов

Вентиляторы электрических машин Для обеспечения циркуляции охлаждающего газа в система вентиляции используются вентиляторы. Вентилятором называется лопастная машина, предназначенная для подачи газов из одной области пространства в другую. По принципу действия вентиляторы разделяют на центробежные и осевые

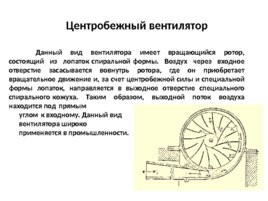
Центробежный вентилятор Данный вид вентилятора имеет вращающийся ротор, состоящий из лопаток спиральной формы. Воздух через входное отверстие засасывается вовнутрь ротора, где он приобретает вращательное движение и, за счет центробежной силы и специальной формы лопаток, направляется в выходное отверстие специального спирального кожуха. Таким образом, выходной поток воздуха находится под прямым углом к входному. Данный вид вентилятора широко применяется в промышленности.

Осевой вентилятор Данный вид вентилятора содержит лопасти (в некоторых случаях вместо понятия «лопасти» применяется понятие «лопатки»), которые перемещают воздух вдоль оси, вокруг которой они вращаются. В виду совпадения направления движения всасываемого и нагнетаемого воздуха, а также, в большинстве случаев, простоты изготовления, этот вид вентилятора является наиболее распространенным.

Диаграммы скоростей частиц воздуха вентиляторов с различной конструкцией лопаток Абсолютная скорость c движения частицы воздуха в междулопаточном пространстве складывается из скорости в относительном движении w и скорости в переносном движении u, т.е.: с u w. Вектор w направлен по касательной к поверхности лопатки в рассматриваемой точке, а вектор u – по касательной к окружности с центром на оси вращения рабочего колеса Угол между направлениями окружной и абсолютной скорости α, однако в расчетах часто используют угол β между касательной в рассматриваемой точке и направлением вектора относительной скорости.

Диаграммы скоростей частиц воздуха вентиляторов с различной конструкцией лопаток - Продолжение Связь между скоростями частиц воздуха выражается диаграммами скоростей Если угол на выходе из рабочего колеса β 2 ,то это вентилятор с загнутыми назад лопатками (рис. б). Если β 2 ,то это вентилятор с радиальными лопатками(рис. в). Если β 2 90 ,то – с загнутыми вперед лопатками (рис. г).

Встроенные вентиляторы Встроенные вентиляторы могут быть центробежными и осевыми. Они устанавливаются на валу или крепятся к вращающимся частям электрических машин. Встроенные вентиляторы не имеют кожухов, могут устанавливаться с направляющими аппаратами и без них.

Вопрос 2.21. Теория идеального центробежного вентилятора. Турбинное уравнение Эйлера. Характеристики давления вентиляторов с различными конструкциями лопаток

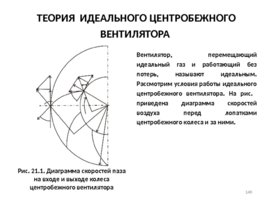
ТЕОРИЯ ИДЕАЛЬНОГО ЦЕНТРОБЕЖНОГО ВЕНТИЛЯТОРА Вентилятор, перемещающий идеальный газ и работающий без потерь, называют идеальным. Рассмотрим условия работы идеального центробежного вентилятора. На рис. приведена диаграмма скоростей воздуха перед лопатками центробежного колеса и за ними. Рис. 21.1. Диаграмма скоростей паза на входе и выходе колеса центробежного вентилятора

На рис.21.1. обозначено: , - абсолютная скорость соответственно при входе на лопатки и при выходе из колеса; , - переносная скорость соответственно на диаметре входа в лопатки и на наружном диаметре колеса; , - относительная скорость воздуха соответственно при входе и выходе; , - тангенциальная составляющая скорости соответственно при входе на лопатки и при выходе; , - радиальная составляющая скорости соответственно при входе и выходе. ТЕОРИЯ ИДЕАЛЬНОГО ЦЕНТРОБЕЖНОГО ВЕНТИЛЯТОРА - Продолжение

К движению в междулопаточном канале применим теорему моментов количества движения: в установившемся движении изменение момента количества движения секундной массы газа при переходе от входного сечения междулопаточного пространства к выходному равно моменту внешних сил , приложенных к потоку между этими сечениями. Внешние силы в колесе центробежного вентилятора прилагаются при помощи системы лопаток. Масса газа, протекающая через междулопаточные каналы за 1 с, равна плотности , умноженной на расход газа , и одинакова для обоих сечений. ТЕОРИЯ ИДЕАЛЬНОГО ЦЕНТРОБЕЖНОГО ВЕНТИЛЯТОРА - Продолжение

ТУРБИННОЕ УРАВНЕНИЕ ЭЙЛЕРА (ОСНОВНОЕ УПРАВЛЕНИЕ ЛОПАСТНЫХ МАШИН) Количество движения в единицу времени на входе, на выходе. Момент количества движения равен произведению количества движения на плечо, т.е. на входе, на выходе. Изменение момента количества движения: где и - плечи абсолютных скоростей и .

Разложим векторы абсолютной скорости и на составляющие и в радиальном и в тангенциальном направлении. Тогда из подобия треугольников и треугольников и следует: Отсюда: Умножим левую правую части на угловую скорость , тогда в левой части получим мощность, передаваемую при помощи вентилятора потоку газа: ТУРБИННОЕ УРАВНЕНИЕ ЭЙЛЕРА (ОСНОВНОЕ УПРАВЛЕНИЕ ЛОПАСТНЫХ МАШИН) - Продолжение

Умножение правой части на с учетом значения окружных скоростей: дает: Так как давление есть энергия жидкости, отнесенная к единице расхода, то мощность, передаваемая газу в междулопаточном пространстве рабочего колеса, , где - полное теоретическое давление, развиваемое вентилятором. Следовательно: ТУРБИННОЕ УРАВНЕНИЕ ЭЙЛЕРА (ОСНОВНОЕ УПРАВЛЕНИЕ ЛОПАСТНЫХ МАШИН) - Продолжение Это соотношение называется турбинным уравнением Эйлера или основным уравнением лопастных машин.

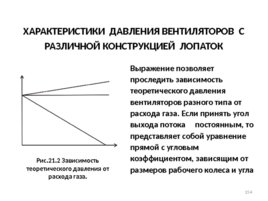
ХАРАКТЕРИСТИКИ ДАВЛЕНИЯ ВЕНТИЛЯТОРОВ С РАЗЛИЧНОЙ КОНСТРУКЦИЕЙ ЛОПАТОК Рис.21.2 Зависимость теоретического давления от расхода газа. Выражение позволяет проследить зависимость теоретического давления вентиляторов разного типа от расхода газа. Если принять угол выхода потока постоянным, то представляет собой уравнение прямой с угловым коэффициентом, зависящим от размеров рабочего колеса и угла

В этом случае характеристики давления будут иметь вид прямых, показанных на рис. Характеристика вентилятора с радиальными лопатками ( 90 ) не зависит от расхода. Характеристика вентилятора с загнутыми назад лопатками ( 90 ) будет иметь отрицательный угловой коэффициент, и с увеличением расхода давление вентилятора падает. Характеристика вентилятора с загнутыми вперед лопатками ( 90) будет иметь положительный угловой коэффициент, и с увеличением расхода давление вентилятора возрастает. ХАРАКТЕРИСТИКИ ДАВЛЕНИЯ ВЕНТИЛЯТОРОВ С РАЗЛИЧНОЙ КОНСТРУКЦИЕЙ ЛОПАТОК - Продолжение

Вопрос 2.22. Потери давления и мощности в центробежном вентиляторе. Баланс энергии и КПД вентилятора. Характеристика давления центробежного вентилятора. Подобие вентиляторов

ПОТЕРИ ДАВЛЕНИЯ И МОЩНОСТИ В ЦЕНТРОБЕЖНОМ ВЕНТИЛЯТОРЕ При работе вентиляторов всегда возникают потери энергии, связанные с передачей механической энергии от привода вентилятора газу, с преобразованием одного вида механической энергии движущегося газа в другой и с те-чением газа через рабочее колесо. Реальное давление , создаваемое центробежным вен-тилятором, всегда меньше теоретического на величину потерь давления в самом вентиляторе.

При этом надо иметь в виду, что теоретическое давление при любом расходе газа через вентилятор равно его значению по формуле (22.2), но во внешней сети может быть использован лишь его избыток по отношению к внутренним потерям, равный . Таким образом, теоретическое давление центробежного вентилятора аналогично ЭДС электрического генератора, давление во внешней сети аналогично напряжению элек-трического генератора.

В вентиляторе имеются следующие виды потерь давления: потери на местных сопротивлениях и трение; потери на входе в рабочее колесо; потери на вихреобразование при протекании пото-ка газа по каналам рабочего колеса; потери при преобразовании кинетической энергии потока, выходящего из рабочего колеса, в статическое давление.

Баланс энергии и КПД вентилятора. Мощность, факти-чески передаваемая вентилятором потоку перемещаемого газа, называется полезной мощностью вентилятора . Полезная мощность равна произведению полезного давле-ния на расход газа : , (22.1) Мощность, потребляемая вентилятором , больше по-лезной мощности на величину потерь, имеющих место при работе вентилятора: , (22.2)

где: - гидравлические потери в рабочем колесе вентиля-тора; - паразитная мощность, отдаваемая рабочим коле-сом, и потоком соседним объемам газа за счет вовлечения их в бесполезное движение; - щелевые потери из-за утечек газа; - механические потери в подшипниках (у встроен-ных вентиляторов отсутствуют).

Коэффициент полезного действия вентилятора: , (22.3) где: - его гидравлический КПД; - гидравлическая мощность; - КПД, учитывающий паразитную мощность; - объемный КПД; - расход газа через рабочее колесо с уче-том утечек через зазоры; - механический КПД, учитывающий механические потери в подшипниках (у встроенных вентиляторов 1).

ХАРАКТЕРИСТИКА ДАВЛЕНИЯ ЦЕНТРОБЕЖНОГО ВЕНТИЛЯТОРА Характеристика давления представляет собой зависи-мость действительного давления р, развиваемого вентиля-тором, от его расхода . По аналогии с электрическим генератором, где зависимость напряжения от тока на-зывается внешней характеристикой, зависимость называют внешней характеристикой вентилятора. Эта ха-рактеристика всегда лежит ниже характеристики его теоре-тического давления из-за потерь давления в вентиляторе. Рассмотрим распределение потерь давления на примере вентилятора с загнутыми назад лопатками (рис. 22.1).

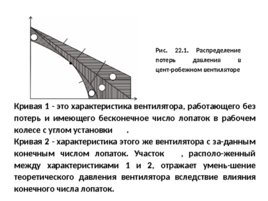
Рис. 22.1. Распределение потерь давления в цент-робежном вентиляторе Кривая 1 - это характеристика вентилятора, работающего без потерь и имеющего бесконечное число лопаток в рабочем колесе с углом установки . Кривая 2 - характеристика этого же вентилятора с за-данным конечным числом лопаток. Участок , располо-женный между характеристиками 1 и 2, отражает умень-шение теоретического давления вентилятора вследствие влияния конечного числа лопаток.

Кривая 3 - характеристика давления вентилятора с конечным числом лопаток при учете потерь на местных сопротивлениях и на трение в рабочем колесе вентилятора. Участок , расположенный между кривыми 2 и 3, характеризует потери на местных сопротивлениях и на трение в проточных частях вентилятора в том числе и междулопаточных каналах рабочего колеса. Участок , расположенный между кривыми 3 и 4, отра-жает потери на входе в рабочее колесо и вихреобразо-вание в каналах рабочего колеса.

Кривая 4 - это характеристика реального, давления вентилятора, или его внешняя характеристика. Точка , в которой соприкасаются кривые 3 и 4, соответствует оптимальному расходу газа, создаваемому вентилятором, при котором потери на вихреобразование в рабочем колесе отсутствуют. Точную внешнюю характеристику центробежного вен-тилятора построить с помощью расчета невозможно, так как сложно учесть все действующие факторы; ее получат по данным испытаний. ХАРАКТЕРИСТИКА ДАВЛЕНИЯ ЦЕНТРОБЕЖНОГО ВЕНТИЛЯТОРА - Продолжение

Полученная система уравнений (2) есть искомое уравнение движения невязкой жидкости – уравнение Эйлера. К трем уравнениям (2) добавляются еще два уравнения, поскольку неизвестных пять, и решается система из пяти уравнений с пятью неизвестными: одним из двух дополнительных уравнений является уравнение неразрывности. Еще одним уравнением является уравнение состояния. Например, для несжимаемой жидкости уравнением состояния может быть условие ρ const. Уравнение состояния должно быть выбрано таким образом, чтобы оно содержало хотя бы одно из пяти неизвестных.

ЭЙЛЕРА УРАВНЕНИЕ В гидромеханике дифференциальное уравнение движения идеальной жидкости в переменных Эйлера. Если давление р , плотность ρ , проекции скоростей частиц жидкости и, v, w к проекции действующей объёмной силы X, Y, Z рассматривать как функции координат х, у, z точек пространства и времени t (переменные Эйлера), то уравнение в проекциях на оси прямоугольной декартовой системы координат принимает вид системы уравнений:

Решение общей задачи гидромеханики в переменных Эйлера сводится к тому, чтобы, зная X, Y, Z, а также начальные и граничные условия, определить как функции х, у, z и t. Для этого к уравнениям Эйлера присоединяют уравнение неразрывности в переменных Эйлера: В случае баротропной жидкости, у которой плотность зависит ρ ϕ(р) только от давления, пятым уравнением будет уравнение состояния (или ρ const, когда жидкость несжимаема).

Вопрос 2.23. Расчет внешней характеристики центробежного вентилятора (суть методик А. Е. Алексеева, И. Ф. Филиппова, ЛЭО «Электросила», М. В. Виноградова и др.). Осевые вентиляторы

Вопрос 2.24. Вентиляционный расчет электрических машин. Задачи вентиляционного расчета. Проектный и проверочный вентиляционные расчеты. Расчет совместной работы вентилятора и вентиляционного тракта. Расчет сложных вентиляционных систем

ВЕНТИЛЯЦИОННЫЙ РАСЧЕТ ЭЛЕКТРИЧЕСКИХ МАШИН Общая задача вентиляционного расчета электрических машин заключается в том, чтобы проверить, как выбранная схема вентиляции и вентилятор обеспечивают допустимую температуру активных частей машины при заданном уровне греющих потерь. В проектном задании на разработку электрической машины, как правило, задается исполнение по степени защиты от внешних воздействий, которое практически предопределяет выбор способа охлаждения и схемы вен-тиляции электрической машины.

ЗАДАЧИ ВЕНТИЛЯЦИОННОГО РАСЧЕТА ЭЛЕКТРИЧЕСКИХ МАШИН Исходными данными для вентиляционного расчета явля-ются схемы вентиляции, размеры каналов вентиляционного тракта, физические свойства охлаждающей среды, класс нагревостойкости применяемых электроизоляционных ма-териалов, потери мощности, которые выделяются в машине при работе и повышают ее температуру, частота вращения вентилятора. Исходя из общей задачи вентиляционного расчета можно выделить несколько частных задач , которые должны решаться при вентиляционном расчете электрической машины. Одна из важнейших задач вентиляционного расчета - оп-ределение суммарного гидравлического сопротивления вентиляционного тракта электрической машины.

Другая задача вентиляционного расчета - определение требуемого расхода охлаждающего газа . Требуемый расход газа определяется количеством отводимых газом потерь, допустимым повышением температуры и теплоемкостью газа: где: - греющие потери, отводимые охлаждающим потоком (известны из электромагнитного расчета машины); - удельная теплоемкость охлаждающего газа, Дж/(кг С); - плотность газа, кг/м З ; - допустимое повышение температуры охлаждающего газа для данного класса нагревостойкости изоляции машины. ЗАДАЧИ ВЕНТИЛЯЦИОННОГО РАСЧЕТА ЭЛЕКТРИЧЕСКИХ МАШИН - Продолжение ,

ПОЛУЧЕНИЕ ИСХОДНЫХ ДАННЫХ ДЛЯ РАСЧЕТА ВЕНТИЛЯТОРА Воспользовавшись законом Адкинсона, можно опреде-лить перепад давлений на суммарном гидравлическом сопротивлении вентиляционного тракта при требуемом расходе газа через машину : Таким образом, требуемый расход охлаждающего га-за и перепад давления , возникающий в машине, являются исходными данными для расчета вентилятора. Расчет вентилятора в зависимости от решаемых задач подразделяется на проектный и поверочный .

При проектном расчете вентилятора должны опреде-ляться основные конструктивные параметры рабочего колеса - наружный и внутренний диаметры, тип, число, размеры и углы установки лопаток. Вентилятор, имеющий выбранные параметры, должен обеспечивать подачу требуемого количества охлаждающего газа при известном суммарном гидравлическом сопротивлении машины. Од-нако для встроенных вентиляторов электрических машин многие из названных параметров ограничены размерами места, в котором должен быть установлен вентилятор. Поэтому основные размеры рабочего колеса вентилятора обычно устанавливаются конструктивно, и при расчетах электрических машин широкое распространение получил поверочный расчет вентилятора. ПОЛУЧЕНИЕ ИСХОДНЫХ ДАННЫХ ДЛЯ РАСЧЕТА ВЕНТИЛЯТОРА - Продолжение

При поверочном расчете вентилятора необходимо про-верить, обеспечит ли вентилятор с данными размерами требуемое давление и расход газа при известном суммарном гидравлическом сопротивлении вентиляцион-ного тракта . Необходимое давление определяют исходя из задан-ного расхода на основе уравнения , или: Соблюдение равенства означает, что потери давления в машине равны давлению, развиваемому вентилятором, т.е. равенство определяет факт равновесия. После этого можно вычислять распределение расходов по отдельным ветвям схемы вентиляции и затраты мощности на вентиляцию. ПОЛУЧЕНИЕ ИСХОДНЫХ ДАННЫХ ДЛЯ РАСЧЕТА ВЕНТИЛЯТОРА - Продолжение .

ОПРЕДЕЛЕНИЕ РАБОЧЕГО РАСХОДА И РАБОЧЕГО ДАВЛЕНИЯ, СОЗДАВАЕМОГО ВЕНТИЛЯТОРОМ Приравнивая -характеристику давления вен-тилятора, с характеристикой давления вентиляционного тракта : , (24.4) получают решение уравнения равновесия в аналитической форме и определяют рабочий расход и рабочее давление , , создаваемое вентилятором.

Давление, создаваемое вентилятором, является сложной функцией расхода газа и не всегда поддается простой анали-тической записи, поэтому, на практике широко используют графический метод решения уравнения (24.4). Этот метод прост и нагляден (рис. 24.1): в координатах , наносят ха-рактеристику давления вентилятора и характерис-тику давления вентиляционного тракта . Точка их пересечения является точкой равновесия, т.е. точкой взаим-ного соответствия потерь давления в машине и давления вентилятора. Рис. 24.1. Пример графического определения рабочего расхода газа ОПРЕДЕЛЕНИЕ РАБОЧЕГО РАСХОДА И РАБОЧЕГО ДАВЛЕНИЯ, СОЗДАВАЕМОГО ВЕНТИЛЯТОРОМ - Продолжение

В результате решения уравнения равновесия (24.4) рабочий расход никогда не бывает в точности равен требуемому расходу . Это объясняется тем, что, во-первых, характеристики вентилятора и вентиляционной сети рассчитаны с определенными погрешностями; во-вторых, очень трудно подобрать вентилятор, чтобы его характеристика пересекалась с характеристикой вентиляционной сети именно в точке ( , ). Поэтому вентиляторы выбирают из условия на 10%. Рис. 24.2. Схема вентиляции машины постоянного тока ОПРЕДЕЛЕНИЕ РАБОЧЕГО РАСХОДА И РАБОЧЕГО ДАВЛЕНИЯ, СОЗДАВАЕМОГО ВЕНТИЛЯТОРОМ - Продолжение

Порядок поверочного вентиляционного расчета. Находят требуемый расход воздуха: Рассчитывают гидравлические сопротивления. Для этого удобно представить вентиляционный тракт в виде упрощенной схемы (рис. 24.3), с помощью которой легко установить причины местных сопротивлений. Затем находят коэффициенты гидравлического сопротивления трения и местных сопротивлений и вычисляют гидравлические сопротивления участков. Эквивалентная гидравлическая схема двигателя постоянного тока (рис. 24.2) приведена на рис. 24.4. м 3 /с

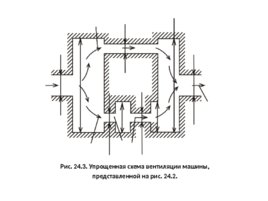
Рис. 24.3. Упрощенная схема вентиляции машины, представленной на рис. 24.2.

ИСХОДНЫЕ ДАННЫЕ ДЛЯ ПОВЕРОЧНОГО ВЕНТИЛЯЦИОННОГО РАСЧЕТА ДПТ Для двигателя постоянного тока известны: Вт - греющие потери; об/мин - частота вращения; Дж/(кг С) - удельная теплоемкость воздуха; кг/м 3 - плотность воздуха; - коэффициент трения в каналах; размеры центробежного вентилятора с радиальными лопатками (м): - наружный диаметр; - внутренний диаметр; - ширина лопаток; значения площадей (м 2 ): - входных окон подшипникового щита; - пространства над коллектором;

- поперечного сечения междуполюсных окон; - пространства над лобовыми частями со стороны заднего подшипникового щита; - поперечного сечения каналов втулки коллек-тора; - пространства под лобовыми частями обмотки якоря; - вентиляционных каналов якоря; - пространства под лобовыми частями обмотки якоря со стороны заднего подшипникового щита; - поперечного сечения выходной решетки; - длина канала междуполюсного окна; - эквивалентный диаметр этого канала; - длина канала втулки коллектора; - эквивалентный диаметр канала втулки кол- лектора; - длина канала якоря; - диаметр канала.

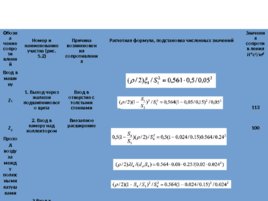
РЕЗУЛЬТАТЫ РАСЧЕТА ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ МПТ (ПРИМЕР К ЭГС, ПРЕДСТАВЛЕННОЙ НА РИС. 5.2 И РИС. 5.4) Обозна чение сопроти влений Номер и наименование участка (рис. 5.2) Причина возникновения сопротивления Расчетная формула, подстановка численных значений Значения сопротив ления Н с 2 /м 8 Вход в машину Z 1 1. Выход через жалюзи подшипникового щита Вход в отверстие с толстыми стенками 113 Z 2 2. Вход в камеру над коллектором Внезапное расширение 100 Проход воздуха между полюсными катушками Z 3 З. Вход в пространство между полюсными катушками Внезапное сужение 411 Z 4 4. Междуполюсные каналы Гидро- динамическое трение 979 Z 5 5. Выход из междуполюсных окон Внезапное расширение 691

окон Проход воздуха через вентиляционные каналы Z 6 6. Вход в вентиляционные каналы коллекторной втулки Внезапное сужение 1802 Z 7 7. Каналы коллекторной втулки Гидродинами-ческое трение 1567 Z 8 8. Выход из каналов коллектора Внезапное сужение 2109 Z 9 9. Выход в аксиальные вентиляционные каналы якоря Внезапное расширение 1345 Z 10 10. Вентиляционные каналы Гидродинами-ческое трение 4661 Z 11 11. Выход из вентиляционных каналов Внезапное расширение 2074 Выход из машины Z 12 12. Проход через выходную решетку Проход через отверстие с толстыми стенками 113 Z 13 13. Выход воздуха в атмосферу Выход в открытый канал 226

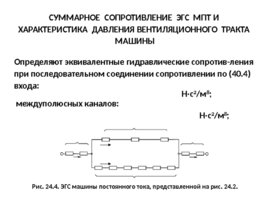
СУММАРНОЕ СОПРОТИВЛЕНИЕ ЭГС МПТ И ХАРАКТЕРИСТИКА ДАВЛЕНИЯ ВЕНТИЛЯЦИОННОГО ТРАКТА МАШИНЫ Определяют эквивалентные гидравлические сопротив-ления при последовательном соединении сопротивлении по (40.4) входа: междуполюсных каналов: Рис. 24.4. ЭГС машины постоянного тока, представленной на рис. 24.2. Н с 2 /м 8 ; Н с 2 /м 8 ;

каналов якоря : выхода : Определяют эквивалентное сопротивление при парал-лельном соединении сопротивлений междуполюсных ка-налов якоря по (40.11): Суммарное сопротивление ЭГС: Находят характеристику давления вентиляционного тракта: Н с 2 /м 8 ; Н с 2 /м 8 . Н с 2 /м 8 . Н с 2 /м 8 . . СУММАРНОЕ СОПРОТИВЛЕНИЕ ЭГС МПТ И ХАРАКТЕРИСТИКА ДАВЛЕНИЯ ВЕНТИЛЯЦИОННОГО ТРАКТА МАШИНЫ - Продолжение

ХАРАКТЕРИСТИКА ДАВЛЕНИЯ, РАБОЧИЙ РАСХОД ВОЗДУХА И РАБОЧЕЕ ДАВЛЕНИЕ, РАЗВИВАЕМОЕ ВЕНТИЛЯТОРОМ Определяют характеристику давления вентилятора, для этого используют методику А. Е. Алексеева. Давление при холостом ходе вентилятора: Па, где: м/с, м/с. Максимальный расход вентилятора: м 3 /с, где: м 2 .

Приравнивая характеристики давления вентилятора и вентиляционного тракта, получают: Характеристика давления вентилятора: рабочий расход вентилятора м 3 /с, рабочее давление, развиваемое вентилятором Па. ХАРАКТЕРИСТИКА ДАВЛЕНИЯ, РАБОЧИЙ РАСХОД ВОЗДУХА И РАБОЧЕЕ ДАВЛЕНИЕ, РАЗВИВАЕМОЕ ВЕНТИЛЯТОРОМ - Продолжение ,

Определяют частичные расходы в параллельных ветвях. При параллельном соединении сопротивлений падения давления на них равны, т.е. откуда: На основании первого закона Кирхгофа: откуда частичные расходы в параллельных ветвях: м 3 /с, м 3 /с. ХАРАКТЕРИСТИКА ДАВЛЕНИЯ, РАБОЧИЙ РАСХОД ВОЗДУХА И РАБОЧЕЕ ДАВЛЕНИЕ, РАЗВИВАЕМОЕ ВЕНТИЛЯТОРОМ - Продолжение ,

Затраты мощности на вентиляцию: Вт. Таким образом, поверочный вентиляционный расчет показал, что при данных размерах вентиляционного тракта данный вентилятор обеспечит требуемый расход воздуха через машину, так как . ХАРАКТЕРИСТИКА ДАВЛЕНИЯ, РАБОЧИЙ РАСХОД ВОЗДУХА И РАБОЧЕЕ ДАВЛЕНИЕ, РАЗВИВАЕМОЕ ВЕНТИЛЯТОРОМ - Продолжение

РАСЧЕТ СЛОЖНЫХ ВЕНТИЛЯЦИОННЫХ СИСТЕМ Непосредственное вычисление суммарного гидравли-ческого сопротивления ЭГС при сложных разветвленных схемах оказывается чрезвычайно громоздким. Поэтому существует много приемов расчета ЭГС гра-фическими и графоаналитическими методами, а также методами последовательных приближений.

Эти методы основаны на двух законах, соответствующих законам Кирхгофа для электрических цепей: 1. Алгебраическая сумма расходов в узле ЭГС равна нулю: 2. Алгебраическая сумма давлений и падений давлений в замкнутом контуре равна нулю: РАСЧЕТ СЛОЖНЫХ ВЕНТИЛЯЦИОННЫХ СИСТЕМ - Продолжение . .

Рис. 24.5. Преобразование треугольника ( а ) гидравлических сопротивлений в звезду ( б ) Наиболее широко распространены метод преобразо-вания треугольника в звезду, графический метод, метод уравнивания потерь давления. Метод преобразования треугольника в звезду. Пусть имеется ЭГС (рис. 24.5, а ) в виде соединения гидравлических сопротивлений в треугольник. Это соединение можно преобразо-вать в эквивалент-ную звезду, как это делают для элек-трических цепей. РАСЧЕТ СЛОЖНЫХ ВЕНТИЛЯЦИОННЫХ СИСТЕМ - Продолжение

Однако с учетом нелинейности сопротивления фор-мулы для преобразования будут более сложными. Полученное решение является приближенным, и об-ратное решение не позволит получить точные значения расходов в отдельных ветвях. На рис. 24.5, б приведено преобразование исходной схемы в эквивалентную звезду. Формулы для пересчета сопротивлений следующие: РАСЧЕТ СЛОЖНЫХ ВЕНТИЛЯЦИОННЫХ СИСТЕМ - Продолжение , , , , ,

Рис. 24.6. Последовательное сложение характеристик давления ( а ) и сопротивления ( б ) Графический метод. Этот метод заключается в том, что при сложении графических характеристик последовательно соединенных элементов складываются их ординаты (рис.24.6, а , б ) при сложении характеристик параллельно соединенных элементов складываются их абсциссы (рис.24.7, а , б ). РАСЧЕТ СЛОЖНЫХ ВЕНТИЛЯЦИОННЫХ СИСТЕМ - Продолжение

При последовательном соединении (рис. 24.8) нагнета-тельного элемента и гидравлического сопротивления из ординаты характеристики, нагнетательного элемента вычитают ординату характеристики гидравлического со-противления , в результате получают характеристику избыточного давления . Рис. 24.7. Параллельное сложение характеристик давления нагнетательных элементов ( а ) и гидравлических сопротивлений ( б ) РАСЧЕТ СЛОЖНЫХ ВЕНТИЛЯЦИОННЫХ СИСТЕМ - Продолжение

Рис. 24.7. Сложение характеристик давления нагнетательного элемента и гидравлического сопротивления при их последовательном соединении. РАСЧЕТ СЛОЖНЫХ ВЕНТИЛЯЦИОННЫХ СИСТЕМ - Продолжение

Вопрос 2.25. Расчет схем вентиляции, содержащих несколько нагнетательных элементов