Презентация - N!. Соединения и правила комбинаторики
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 96%
- Слайдов: 56
- Просмотров: 6529
- Скачиваний: 3280
- Размер: 4.42 MB
- Онлайн: Да
- Формат: ppt / pptx
Примеры похожих презентаций
 Как из букв составляются слоги, из слогов – слова, так из правильного соединения слов составляются предложения
Как из букв составляются слоги, из слогов – слова, так из правильного соединения слов составляются предложения Соединение брусков
Соединение брусков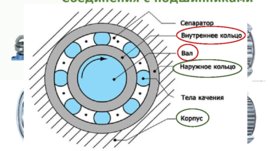 Соединения с подшипниками качения
Соединения с подшипниками качения Воспитательные, развивающие и обучающие задачи: в чем разница и как их правильно формулировать
Воспитательные, развивающие и обучающие задачи: в чем разница и как их правильно формулировать Правильная осанка - залог здоровья
Правильная осанка - залог здоровья Настольный теннис - Правила игры
Настольный теннис - Правила игры Правила обращения с веществами и лабораторным оборудованием
Правила обращения с веществами и лабораторным оборудованием
Слайды и текст этой онлайн презентации
Слайд 1

n!
Соединения и правила комбинаторики
Волошина Н.Н., *
Соединения и правила комбинаторики
Волошина Н.Н., *
Слайд 2

Множества
Теория соединений, или, как ее еще называют, комбинаторика, - это раздел элементарной алгебры, где изучаются некоторые операции над конечными множествами и решаются задачи, связанные с этими операциями. Комбинаторика - раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями. Термин «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять».
Теория соединений, или, как ее еще называют, комбинаторика, - это раздел элементарной алгебры, где изучаются некоторые операции над конечными множествами и решаются задачи, связанные с этими операциями. Комбинаторика - раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями. Термин «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять».
Слайд 3

Термин "комбинаторика" был введён
в математический обиход знаменитым
Лейбницем.
В 1666 году Лейбниц опубликовал
«Рассуждения о комбинаторном
искусстве».
Комбинаторика становится наукой лишь
в XVII в. в период, когда возникла теория вероятности.
Чтобы решать теоретико-вероятностные задачи, нужно было уметь подсчитывать число различных комбинаций, подчиненных тем или иным условиям.
Комбинаторными задачами интересовались и математики, занимавшиеся составлением и разгадыванием шифров, изучением древних письменностей.
Теперь комбинаторика находит приложения во многих областях науки: в биологии, где она применяется для изучения состава белков и ДНК, в химии, механике сложных сооружений и т. д .
Слайд 4

Понятия множества - одно из неопределяемых основных понятий в математике.
С этим понятием встречаемся во всех ее разделах.
Так, в арифметике рассматривают множество натуральных чисел, множество простых чисел; в алгебре - множество многочленов, корней данного уравнения и т.п.
Объекты, составляющие множество, называются элементами этого множества.
Множество, состоящее из конечного числа элементов, называется конечным.
Такими множествами являются множество всех двузначных чисел, множество вершин данного многоугольника, множество его диагоналей и т.д.
Множество, содержащее неограниченное количество элементов, называется бесконечным.
Бесконечным множеством, например, является множество всех натуральных чисел, всех простых чисел и т.д.
Множество, не содержащее элементов, называется пустым.
Слайд 5

Если всякий элемент множества В есть элемент множества А, то множество В называют подмножеством множества А.
Подмножеством множества А считают также пустое множество и само множество А; их называют несобственными подмножествами; остальные подмножества называют собственными.
Отношения между множествами наглядно представляют при помощи кругов Эйлера
Слайд 6
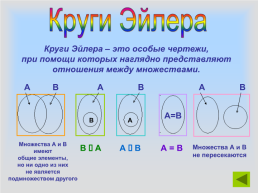
Круги Эйлера
Круги Эйлера – это особые чертежи, при помощи которых наглядно представляют отношения между множествами.
А
В
А
В
А
В
А=В
В
А
Множества А и В имеют общие элементы, но ни одно из них не является подмножеством другого
В М А
А М В
А = В
Множества А и В не пересекаются
Круги Эйлера – это особые чертежи, при помощи которых наглядно представляют отношения между множествами.
А
В
А
В
А
В
А=В
В
А
Множества А и В имеют общие элементы, но ни одно из них не является подмножеством другого
В М А
А М В
А = В
Множества А и В не пересекаются
Слайд 7

Множество М = {а, b, с, d, ...} называется упорядоченным, если между его элементами установлено некоторое соотношение а < b (читают: "а предшествует b"), имеющее следующие свойства:
1) для каких-либо двух элементов а и b действительно одно и только одно из соотношений a = b, а < b, b > а;
2) для всяких трех элементов а, b и с из соотношений а > b и b > с следует соотношение а > с.
Слайд 8

Комбинаторные задачи
Перестановки Сочетания Размещения Решение примеров и задач Правила комбинаторики Комбинаторный практикум Комбинации с повторением
Перестановки Сочетания Размещения Решение примеров и задач Правила комбинаторики Комбинаторный практикум Комбинации с повторением
Слайд 9

Перестановки
Пусть мы имеем множество М, состоящее из n элементов: a₁, а₂, а₃, ..., аn. Если переставлять эти элементы всеми возможными способами, оставляя неизменным их общее число, получим несколько последовательностей: а1 а2 a3 ... an, а2 а1 а3 ... аn, аn а3 а2 ... a1 и т.д. Каждую из этих последовательностей называют перестановкой из данных n элементов.
Пусть мы имеем множество М, состоящее из n элементов: a₁, а₂, а₃, ..., аn. Если переставлять эти элементы всеми возможными способами, оставляя неизменным их общее число, получим несколько последовательностей: а1 а2 a3 ... an, а2 а1 а3 ... аn, аn а3 а2 ... a1 и т.д. Каждую из этих последовательностей называют перестановкой из данных n элементов.
Слайд 10

Пример.
Ниже приведены 6 всевозможных перестановок из букв а, b и с:
abc, асb, bас, bса, cab, сbа.
Итак, перестановкой из n элементов называется всякая конечная последовательность, которая получается
в результате упорядоченности некоторого конечного множества, состоящего
из n элементов.
Если множество имеет некоторое число элементов, то его можно упорядочить несколькими способами.
Число всех перестановок из n элементов обозначается Рn.
Слайд 11

Это число равно произведению всех целых чисел от 1 до n включительно:
Рn = 1 · 2 · 3 · 4 ... (n - 1) · n.
Произведение n первых натуральных чисел принято обозначать символом n!:
1 · 2 · 3 · 4 · 5 · ... · n = n!
Символ n! читают "эн факториал".
Это слово происходит от латинского factor,
что значит - множитель.
Итак, Рn = n!
Верна также следующая формула:
Pn = n · Pn-1
Слайд 12

Примечание.
При n = 1 в выражении 1 · 2 · 3, ... n остается одно число 1. Поэтому принимается (в качестве определения): 1! = 1. При n = 0 выражение 1 · 2, ..., n вовсе лишается смысла. Однако принимается (в качестве определения): 0! = 1.
При n = 1 в выражении 1 · 2 · 3, ... n остается одно число 1. Поэтому принимается (в качестве определения): 1! = 1. При n = 0 выражение 1 · 2, ..., n вовсе лишается смысла. Однако принимается (в качестве определения): 0! = 1.
Слайд 13

Пример 1
Каким числом способов можно расставить 8 книг на полке из 8 мест? Решение: Р8 = 8! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40320.
Каким числом способов можно расставить 8 книг на полке из 8 мест? Решение: Р8 = 8! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40320.
Слайд 14

Сочетания - комбинации
Пусть имеем множество М, состоящее из n различных элементов. Всякое подмножество множества М, содержащее k элементов (k = 0, 1, 2, ..., n), называется сочетанием или комбинацией из данных n элементов по k элементов. Из определения следует, что два различных сочетания из данных n элементов по k элементов отличаются по крайней мере одним элементом.
Пусть имеем множество М, состоящее из n различных элементов. Всякое подмножество множества М, содержащее k элементов (k = 0, 1, 2, ..., n), называется сочетанием или комбинацией из данных n элементов по k элементов. Из определения следует, что два различных сочетания из данных n элементов по k элементов отличаются по крайней мере одним элементом.
Слайд 15

Пример.
Из множества цифр 1, 2, 3, 4 можно образовать такие сочетания по два элемента:
1, 2; 1, 3; 1, 4; 2, 3; 2, 4; 3, 4.
Число различных сочетаний из n элементов по k обозначается символом:
combinatio от combinare (лат.) - соединять
Но иногда вместо пишут:
Слайд 16

Число всех сочетаний из n элементов по k элементов, где 1 ≤ k ≤ n, равно произведению k последовательных натуральных чисел, из которых наибольшее есть n, деленному на произведение последовательных натуральных чисел от 1 до k
Слайд 17

Формулу для можно записать в ином виде. Умножив числитель и знаменатель дроби в правой части ее на произведение 1 · 2 · 3 ... (n - k), получим: или
Слайд 18

Примечание
Из n элементов можно составить только одно сочетание, содержащее все n элементов, поэтому Формула для дает это значение только в том случае, если принять 0! за 1. В качестве определения принимается, что Принято также считать, что
Из n элементов можно составить только одно сочетание, содержащее все n элементов, поэтому Формула для дает это значение только в том случае, если принять 0! за 1. В качестве определения принимается, что Принято также считать, что
Слайд 19

Пример 2
Из 15 туристов надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор? Решение: Можно оформить решение более рационально:
Из 15 туристов надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор? Решение: Можно оформить решение более рационально:
Слайд 20

Свойства сочетаний
1) Число сочетаний из n элементов по k элементов равно числу сочетаний из n элементов по n - k элементов, т.е. Это соотношение позволяет упростить нахождение числа сочетаний из n элементов по k, когда k превосходит Пример:
1) Число сочетаний из n элементов по k элементов равно числу сочетаний из n элементов по n - k элементов, т.е. Это соотношение позволяет упростить нахождение числа сочетаний из n элементов по k, когда k превосходит Пример:
Слайд 21

Свойства сочетаний
2) Число сочетаний из n элементов по k элементов равно числу сочетаний из n - 1 элементов по k элементов, прибавленному к числу сочетаний из n - 1 элементов по k - 1 элементов, т.е. правило Паскаля: Комбинаторные тождества:
2) Число сочетаний из n элементов по k элементов равно числу сочетаний из n - 1 элементов по k элементов, прибавленному к числу сочетаний из n - 1 элементов по k - 1 элементов, т.е. правило Паскаля: Комбинаторные тождества:
Слайд 22

Слайд 23

Слайд 24

Размещения
Возьмем какое-либо множество М, состоящее из n элементов. Всякое упорядоченное подмножество, содержащее k элементов данного множества n элементов, называется размещением из n элементов по k элементов. Таким образом, два разных размещения из данных n элементов по k отличаются друг от друга или составом элементов, входящих в них, или порядком из размещения.
Возьмем какое-либо множество М, состоящее из n элементов. Всякое упорядоченное подмножество, содержащее k элементов данного множества n элементов, называется размещением из n элементов по k элементов. Таким образом, два разных размещения из данных n элементов по k отличаются друг от друга или составом элементов, входящих в них, или порядком из размещения.
Слайд 25

Из трех цифр 1, 2, 3 можно образовать такие размещения по два:
1, 2; 2, 1; 1, 3; 3, 1; 2, 3; 3, 2.
Число размещений из n элементов по k обозначается символом
Arrangement (франц.) - размещения.
Слайд 26

Число всевозможных размещений
из n элементов по k равно произведению k последовательных целых чисел, из которых наибольшее есть n, т.е.
или
Слайд 27

Пример 3
В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в день? Решение: Всевозможные распределения уроков в день представляют собой, очевидно, всевозможные размещения из 10 элементов по 5; поэтому всех способов распределения должно быть:
В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в день? Решение: Всевозможные распределения уроков в день представляют собой, очевидно, всевозможные размещения из 10 элементов по 5; поэтому всех способов распределения должно быть:
Слайд 28

Решение примеров и задач
на соединения
n! = n(n-1)(n-2)…4·3·2·1
n! = n(n-1)(n-2)…4·3·2·1
Слайд 29

Упростить выражение: Решение:
Слайд 30

2. Решить уравнение: Решение: (x + 1)(х + 2) = 110 или x2 + 3x - 108 = 0, Ответ: х = 9.
Слайд 31
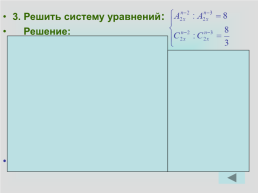
3. Решить систему уравнений:
Решение:
Ответ: n = 5, x = 5
Слайд 32
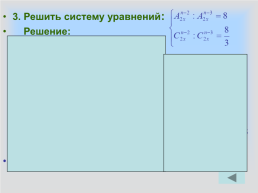
3. Решить систему уравнений:
Решение:
Ответ: n = 5, x = 5
Слайд 33

4. Число перестановок из n букв относится к числу перестановок из n + 2 букв, как 0,1 к 3. Найти n.
Решение:
По условию
=> (n + 1)(n + 2) = 30
n2 + 3n – 28 = 0
Ответ: n = 4
Слайд 34

5. Число сочетаний из n элементов по 3
в 5 раз меньше числа сочетаний из n + 2 элементов по 4. Найти n.
Решение:
По условию
=> 20(n - 2) = n2 + 3n + 2
n2 – 17n + 42 = 0
Ответ: {3; 14}
Это выражение можно не записывать!
Это выражение можно не записывать!
Слайд 35

6. Сколькими разными способами собрание, состоящее из 40 человек, может избрать из своего числа председателя собрания, его заместителя и секретаря?
Решение:
Избрать определенные три человека из 40 человек можно так:
а - председатель, а - секретарь,
b - секретарь, b - председатель,
с - зам. председателя; с - зам. председателя
и т.д., => количество разных способов будет:
Слайд 36

7. На плоскости расположено 10 точек так, что из них никакие 3, за исключением одной тройки точек, не лежат на одной прямой. Сколько разных прямых можно провести через эти точки?
Решение:
Если бы 3 точки не лежали на одной прямой,
то всего можно было бы провести прямых.
Если при этом 1 точка перемещается так, что будет на одной прямой с 2 другими точками, то из 3 разных прямых получим одну.
Итак, всего прямых можно провести:
Слайд 37

Правило умножения строгое
Если объект А1 может быть выбран n1 способами, затем для каждого из таких выборов объекта А1 другого объекта А2 может быть n2 способов, затем для каждого из таких выборов и объекта А1, и объекта А2 – III объект А3 может быть выбран n3 способами, и т.д., включая Аm, который может быть выбран nm способами, то объект, состоящий в выборе всех m объектов вместе, т.е. объект А1, и А2, и А3, … и Аm может быть выбран n1 · n2 · n3 · … · nm способами
Если объект А1 может быть выбран n1 способами, затем для каждого из таких выборов объекта А1 другого объекта А2 может быть n2 способов, затем для каждого из таких выборов и объекта А1, и объекта А2 – III объект А3 может быть выбран n3 способами, и т.д., включая Аm, который может быть выбран nm способами, то объект, состоящий в выборе всех m объектов вместе, т.е. объект А1, и А2, и А3, … и Аm может быть выбран n1 · n2 · n3 · … · nm способами
Слайд 38
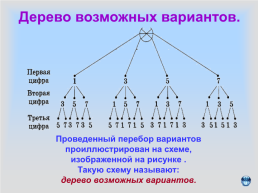
Дерево возможных вариантов.
Проведенный перебор вариантов проиллюстрирован на схеме, изображенной на рисунке . Такую схему называют: дерево возможных вариантов.
Проведенный перебор вариантов проиллюстрирован на схеме, изображенной на рисунке . Такую схему называют: дерево возможных вариантов.
Слайд 39

Комбинаторное правило умножения
Пусть имеется n элементов и требуется выбрать один за другим некоторые m элементов. Если I элемент можно выбрать n1 способами, после чего II элемент можно выбрать из оставшихся элементов n2 способами, затем III элемент — n3 способами и т. д., то число способов, которыми могут быть выбраны все m элементов, равно произведению n1 · n2 · n3 · … · nm
Пусть имеется n элементов и требуется выбрать один за другим некоторые m элементов. Если I элемент можно выбрать n1 способами, после чего II элемент можно выбрать из оставшихся элементов n2 способами, затем III элемент — n3 способами и т. д., то число способов, которыми могут быть выбраны все m элементов, равно произведению n1 · n2 · n3 · … · nm
Слайд 40

Правило для 2-х элементов
Правило умножения, иначе называемое правилом «и» — одно из основных правил комбинаторики. Если элемент A можно выбрать n способами и, при любом выборе A (т.е. независимо), элемент B можно выбрать m способами, то пару (A, B) можно выбрать n · m способами.
Правило умножения, иначе называемое правилом «и» — одно из основных правил комбинаторики. Если элемент A можно выбрать n способами и, при любом выборе A (т.е. независимо), элемент B можно выбрать m способами, то пару (A, B) можно выбрать n · m способами.
Слайд 41
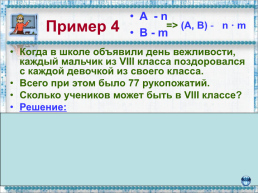
A - n
B - m
Пример 4
=> (A, B) - n · m
Когда в школе объявили день вежливости, каждый мальчик из VIII класса поздоровался с каждой девочкой из своего класса. Всего при этом было 77 рукопожатий. Сколько учеников может быть в VIII классе? Решение: Т.к. 77 = 7 • 11, то, по правилу умножения для комбинаторных задач, в классе может быть или 7 девочек и 11 мальчиков, или 7 мальчиков и 11 девочек, т.e. всего ребят 7 + 11 = 18 Ответ: 18
Пример 4
=> (A, B) - n · m
Когда в школе объявили день вежливости, каждый мальчик из VIII класса поздоровался с каждой девочкой из своего класса. Всего при этом было 77 рукопожатий. Сколько учеников может быть в VIII классе? Решение: Т.к. 77 = 7 • 11, то, по правилу умножения для комбинаторных задач, в классе может быть или 7 девочек и 11 мальчиков, или 7 мальчиков и 11 девочек, т.e. всего ребят 7 + 11 = 18 Ответ: 18
Слайд 42
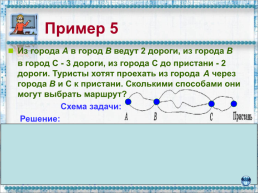
Пример 5
Из города А в город В ведут 2 дороги, из города В в город С - 3 дороги, из города С до пристани - 2 дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут? Схема задачи: Решение: Путь из А в В можно выбрать 2-мя способами. Далее в каждом случае можно проехать из В в С 3-мя способами. Значит, имеем 2 · 3 вариантов маршрута из А в С. Т.к. из С на пристань можно попасть 2-мя способами, то всего 2 · 3 · 2 = 12 способов выбора туристами маршрута из города А к пристани.
Из города А в город В ведут 2 дороги, из города В в город С - 3 дороги, из города С до пристани - 2 дороги. Туристы хотят проехать из города А через города В и С к пристани. Сколькими способами они могут выбрать маршрут? Схема задачи: Решение: Путь из А в В можно выбрать 2-мя способами. Далее в каждом случае можно проехать из В в С 3-мя способами. Значит, имеем 2 · 3 вариантов маршрута из А в С. Т.к. из С на пристань можно попасть 2-мя способами, то всего 2 · 3 · 2 = 12 способов выбора туристами маршрута из города А к пристани.
Слайд 43

Правило сложения
Пусть даны m действий А1, А2, А3, …, Аm таких, что выполнение любого из них не зависит от выполнения остальных. Если: действие А1 можно выполнить n1 способами, А2 ------ n2 способами, -------------------------------, Аm ------ nm способами, то действие, состоящее в том, что выполняется одно любое из действий, можно выполнить n1 + n2 + …. + nm способами
Пусть даны m действий А1, А2, А3, …, Аm таких, что выполнение любого из них не зависит от выполнения остальных. Если: действие А1 можно выполнить n1 способами, А2 ------ n2 способами, -------------------------------, Аm ------ nm способами, то действие, состоящее в том, что выполняется одно любое из действий, можно выполнить n1 + n2 + …. + nm способами
Слайд 44
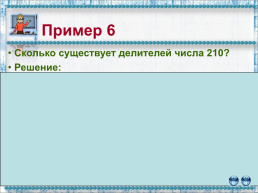
Пример 6
Сколько существует делителей числа 210? Решение: 210 = 2 · 3 · 5 · 7 Число делителей из произведения 2-х простых множителей (6,10,14,15,21,35) из 3-х простых множителей (30,42,70,105) из простых делителей – 4 (2,3,5,7) еще делители 1 и 210 => по правилу сложения: 6 + 4 + 4 + 1 + 1 = 16
Сколько существует делителей числа 210? Решение: 210 = 2 · 3 · 5 · 7 Число делителей из произведения 2-х простых множителей (6,10,14,15,21,35) из 3-х простых множителей (30,42,70,105) из простых делителей – 4 (2,3,5,7) еще делители 1 и 210 => по правилу сложения: 6 + 4 + 4 + 1 + 1 = 16
Слайд 45

Комбинаторный практикум
1. Найти число диагоналей выпуклого десятиугольника. Решение: Вершины десятиугольника образуют совокупность 10 точек плоскости, из которых любые три не лежат на одной прямой. Соединяя всякую пару этих точек отрезком прямой, получаем отрезков, 10 из которых являются сторонами многоугольника, а другие 35 - его диагоналями.
1. Найти число диагоналей выпуклого десятиугольника. Решение: Вершины десятиугольника образуют совокупность 10 точек плоскости, из которых любые три не лежат на одной прямой. Соединяя всякую пару этих точек отрезком прямой, получаем отрезков, 10 из которых являются сторонами многоугольника, а другие 35 - его диагоналями.
Слайд 46

2. Сколько возможных способов для образования дозора из трех солдат и одного офицера, если есть 80 солдат и 3 офицера?
Решение:
При одном офицере и 80 солдатах можно образовать дозор
При 3-х офицерах число способов будет
в 3 раза больше
Слайд 47

3. В кафе предлагают два первых блюда: борщ, рассольник. И четыре вторых блюда: гуляш, кебаб, суши, пельмени.
Укажите все обеды из двух блюд,
которые может заказать посетитель.
Проиллюстрируйте ответ,
построив дерево возможных вариантов.
Решение:
Обозначим первые блюда Б, Р; вторые – Г, К, С, П. Имеем 4 выбора вторых и 2 выбора первых блюд. Значит существует 4·2=8 вариантов заказа обеда изданных блюд.
Дерево возможных вариантов.
+
Слайд 48

4. Сколько возможных способов распределения 6 разных предметов между тремя лицами, так чтобы каждое из них получило 2 предмета?
Решение:
Одно лицо предметов
Пусть лица А, В, С получили при одном способе распределения по два предмета так:
А - аb, B - cd, С - ef.
Поменяв местами собственников этих предметов, получим Р₃ способов распределения, что соответствует одной комбинации из 6 элементов по 2.
Итак, всего способов распределения будет .
Слайд 49
5. Сколько может быть случаев выбора двух карандашей и трех ручек из 5 разных карандашей и 5 разных ручек?
Решение:
Выбор
Из 5 карандашей 2 карандаша –
Из 5 ручек 3 ручки –
=>
Слайд 50

6. Среди сочетаний из 10 букв а, b, с, ... по 4 сколько таких, что не содержат букву а?, буквы а и b?
Решение:
Чтобы вычислить количество сочетаний из 10 букв а, b, с, ... по 4, которые не содержат буквы а, надо подсчитать число сочетаний из 9 букв b, с, ... по 4; их будет
Тогда число сочетаний из 10 по 4, не содержащих букв а и b, будет
Слайд 51

7. Сколько различных натуральных чисел можно составить из цифр 0, 1, 2, 3, 4, если в каждое число входит каждая из данных цифр не более одного раза?
Решение:
Различными однозначными числами, исключая нуль, будут
Если бы среди данных цифр не было нуля, то число различных двузначных чисел было бы равно
Но так как среди них есть нуль, то в числе размещений из этих пяти цифр по две есть однозначные числа, это те, которые начинаются с нуля. Число их равно
Значит, различных двузначных чисел получится
Аналогично найдем, что число различных трех-, четырех- и пятизначных чисел будет соответственно
Всего получится 4 + 16 + 48 + 96 + 96 = 260 чисел.
Слайд 52

8. В шахматном турнире двое из участников выбыли, сыграв по три партии каждый, и потому на турнире было сыграно всего 84 партии.
Сколько было участников первоначально?
Решение:
Пусть искомое число участников турнира было х. Полностью сыграли друг с другом по партии лишь х-2 участников (двое выбыли) и число этих партий, очевидно, равно числу
Это число партии вместе с шестью сыгранными двумя выбывшими участниками составило 84 партии. Отсюда получаем уравнение
=> x² - 5х - 150 = 0, x = 15; x = -10 не удовл. реш. зад.
Ответ. 15.
Примечание. В решении предполагается, что выбывшие игроки друг с другом не играли. Это действительно так, потому что уравнение
не имеет решений.
Слайд 53

В перестановках, сочетаниях и размещениях, которые мы выше рассмотрели, элементы, входящие в них, не повторяются, и поэтому их называют соответственно перестановками, комбинациями, размещениями
без повторений.
В математике рассматривают
также перестановки,
комбинации и размещения
с повторениями…
Слайд 54

Слайд 55

Слайд 56

^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
