Презентация - Замечательные кривые

ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ
Вы узнаете о некоторых поистине замечательных кривых, населяющих удивительный мир геометрии…

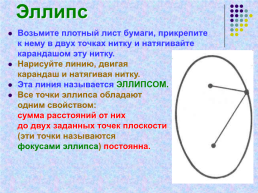
Эллипс
Возьмите плотный лист бумаги, прикрепите к нему в двух точках нитку и натягивайте карандашом эту нитку. Нарисуйте линию, двигая карандаш и натягивая нитку. Эта линия называется ЭЛЛИПСОМ. Все точки эллипса обладают одним свойством: сумма расстояний от них до двух заданных точек плоскости (эти точки называются фокусами эллипса) постоянна.

На самом деле эллипсы в нашей жизни встречаются гораздо чаще, чем кажется. Например, когда мы режем наискосок колбасу, то получающийся кусок имеет эллиптическую форму. Планеты движутся по эллиптическим орбитам, причем Солнце находится в одном из фокусов. У эллипса есть целый ряд свойств, которые могут иметь самые неожиданные применения. Так, если мы сделаем зеркало в форме эллипса и поместим в одном из фокусов источник света, то лучи, отразились от зеркала, соберутся в другом фокусе.

Окружность
R
O
Окружность – частный случай эллипса. Она получается, если фокусы эллипса совпадают.

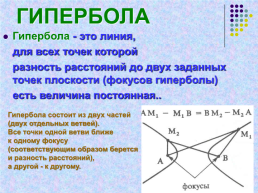
ГИПЕРБОЛА
Гипербола - это линия, для всех точек которой разность расстояний до двух заданных точек плоскости (фокусов гиперболы) есть величина постоянная..
Гипербола состоит из двух частей (двух отдельных ветвей). Все точки одной ветви ближе к одному фокусу (соответствующим образом берется и разность расстояний), а другой - к другому.

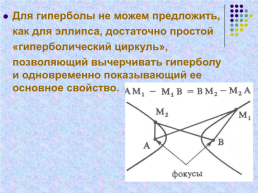
Для гиперболы не можем предложить, как для эллипса, достаточно простой «гиперболический циркуль», позволяющий вычерчивать гиперболу и одновременно показывающий ее основное свойство.

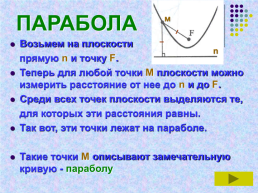
ПАРАБОЛА
м
Возьмем на плоскости прямую n и точку F. Теперь для любой точки M плоскости можно измерить расстояние от нее до n и до F. Среди всех точек плоскости выделяются те, для которых эти расстояния равны. Так вот, эти точки лежат на параболе. Такие точки М описывают замечательную кривую - параболу
n

Длина отрезка FM равна длине перпендикуляра, опущенного из М на прямую n. Эта замечательная кривая не так уж редка в природе. Например, камень, брошенный человеком под углом к поверхности Земли, описывает параболу.
м
n

Все только что рассмотренные линии: эллипс, гипербола и парабола объединяются общим свойством. Каждая из них может быть получена при пересечении конуса плоскостью. Их поэтому называют КОНИЧЕСКИМИ СЕЧЕНИЯМИ.

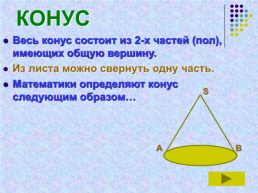
КОНУС
Весь конус состоит из 2-х частей (пол), имеющих общую вершину. Из листа можно свернуть одну часть. Математики определяют конус следующим образом…
S
A
B

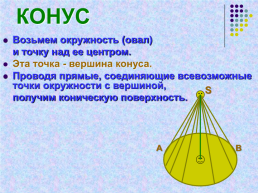
КОНУС
Возьмем окружность (овал) и точку над ее центром. Эта точка - вершина конуса. Проводя прямые, соединяющие всевозможные точки окружности с вершиной, получим коническую поверхность.
S
A
B

Конус можно пересечь плоскостью по окружности. Наклоняя плоскость сечения, получим эллипс (плоскость 1). Увеличивая наклон плоскости, получаем все более вытянутые эллипсы. В конце концов эллипс превратится в параболу. При этом по-прежнему сечением задеваем лишь одну «полу» конуса (плоскость 2) Наклоняя плоскость дальше, пересекаем и вторую «полу». Появятся 2 ветви, парабола перейдет в гиперболу (плоскость 3).

CПИРАЛЬ АРХИМЕДА
Пусть по радиусу равномерно вращающегося диска ползет муравей. Проползая вперед, он одновременно смещается в сторону вращения диска. Таким образом, путь муравья представляет кривую на рисунке. Она называется: СПИРАЛЬ АРХИМЕДА (с латыни спираль означает изгиб, извив).

CИНУСОИДА
Сделайте из плотной бумаги, свернув ее несколько раз, трубочку. Разрежьте эту трубочку наклонно. Если трубочку не разворачивать, то в сечении будет эллипс. Если развернуть одну из частей трубочки, то получится одна из замечательных кривых - СИНУСОИДА.

Домашнее задание:
Подготовить сообщение или презентацию о замечательных кривых: КАРДИОИДА ЦИКЛОИДА ГИПОЦИКЛОИДЫ