Презентация - Построение треугольника по двум сторонам и углу между ними

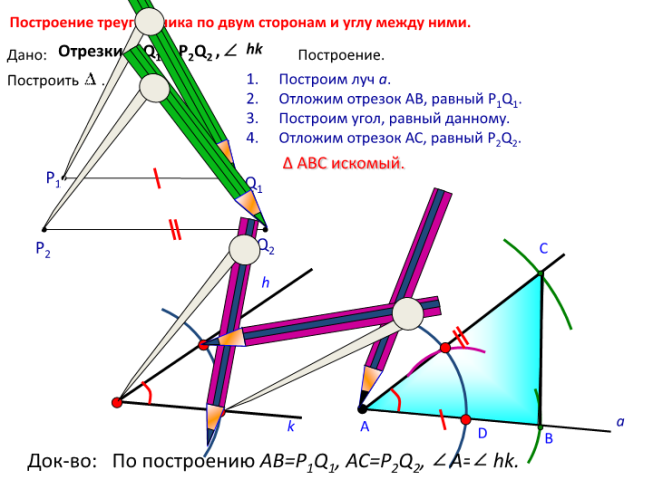
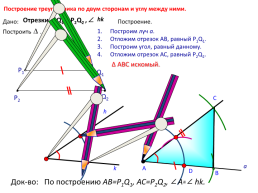
Построение треугольника по двум сторонам и углу между ними.
hk
Отрезки Р1Q1 и Р2Q2 ,
Дано:
Построение.
Построим луч а. Отложим отрезок АВ, равный P1Q1. Построим угол, равный данному. Отложим отрезок АС, равный P2Q2.
Построить .
Δ АВС искомый.
P1
Q1
Q2
P2
С
h
а
k
А
D
В
Док-во: По построению AB=P1Q1, AC=P2Q2, A= hk.

При любых данных отрезках AB=P1Q1, AC=P2Q2 и данном неразвернутом hk искомый треугольник построить можно. Так как прямую а и точку А на ней можно выбрать произвольно, то существует бесконечно много треугольников, удовлетворяющих условиям задачи. Все эти треугольники равны друг другу (по первому признаку равенства треугольников), поэтому принято говорить, что данная задача имеет единственное решение.

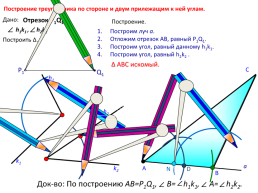
Построение треугольника по стороне и двум прилежащим к ней углам.
Дано:
Отрезок Р1Q1
Построение.
h1k1 , h2k2
Построим луч а. Отложим отрезок АВ, равный P1Q1. Построим угол, равный данному h1k1. Построим угол, равный h2k2 .
Построить Δ.
Δ АВС искомый.
P1
С
Q1
h1
h2
k1
а
k2
А
N
D
В
Док-во: По построению AB=P1Q1, В= h1k1, А= h2k2.

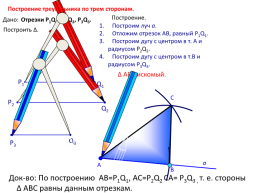
Построение треугольника по трем сторонам.
Построение.
Дано:
Отрезки Р1Q1, Р2Q2, P3Q3.
Построим луч а. Отложим отрезок АВ, равный P1Q1. Построим дугу с центром в т. А и радиусом Р2Q2. Построим дугу с центром в т.В и радиусом P3Q3.
Построить Δ.
Δ АВС искомый.
P1
Q1
С
P2
Q2
Q3
P3
а
А
В
Док-во: По построению AB=P1Q1, AC=P2Q2 CA= P3Q3 , т. е. стороны Δ ABC равны данным отрезкам.

Задача не всегда имеет решение. Во всяком треугольнике сумма любых двух сторон больше третьей стороны, поэтому если какой-нибудь из данных отрезков больше или равен сумме двух других, то нельзя построить треугольник, стороны которого равнялись бы данным отрезкам.