Презентация - Гармонические колебания

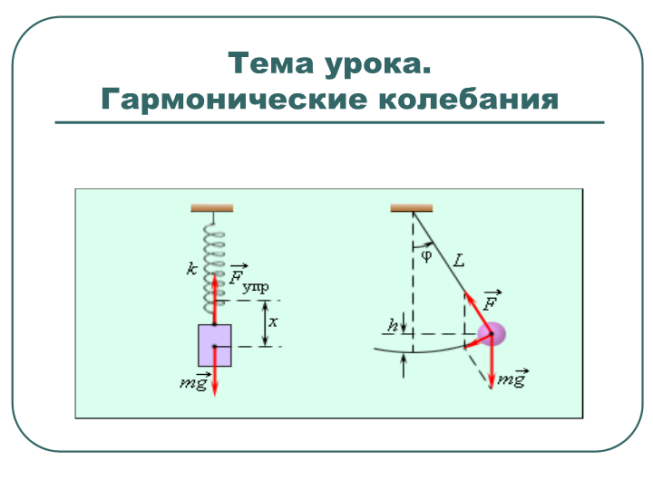
Тема урока. Гармонические колебания

Давайте вспомним
Колебания – … процесс, который частично или полностью повторяется через некоторый промежуток времени. Например, …

Давайте вспомним
Амплитуда- … максимальное отклонение тела от положения равновесия.
Хmax=0,2 см

Давайте вспомним
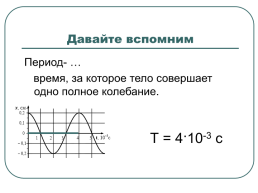
Период- … время, за которое тело совершает одно полное колебание.
Т = 4·10-3 с

Давайте вспомним

Давайте вспомним
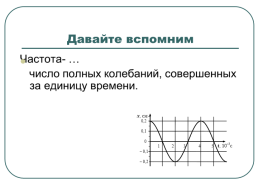
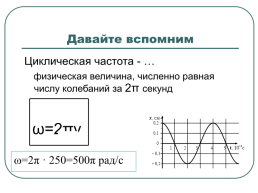
Циклическая частота - … физическая величина, численно равная числу колебаний за 2π секунд
ω=2π · 250=500π рад/с

Давайте вспомним
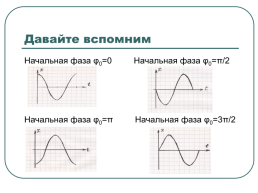
Начальная фаза φ0=0
Начальная фаза φ0=π/2
Начальная фаза φ0=π
Начальная фаза φ0=3π/2

Уравнение гармонических колебаний
Гармонические колебания – это колебания, происходящие по закону синуса или косинуса
x = xm cos (ωt + φ0) Xm – амплитуда колебаний φ0 – начальная фаза колебаний ω – циклическая частота ω=2πν φ = ωt +  φ0 – фаза колебаний в данный момент времени

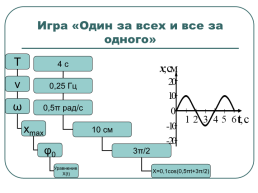
Игра «Один за всех и все за одного»

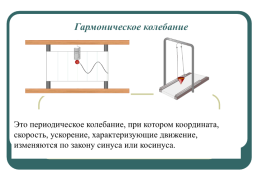
Гармоническое колебание
Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

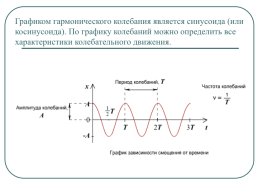
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Уравнение гармонического колебания
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение

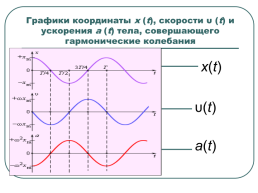
Графики координаты x (t), скорости υ (t) и ускорения a (t) тела, совершающего гармонические колебания
x(t)
υ(t)
a(t)

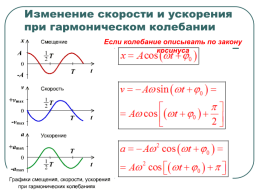
Изменение скорости и ускорения при гармоническом колебании
Если колебание описывать по закону косинуса

Максимальные значения скорости и ускорения
Задача 1. Напишите уравнения гармонических колебаний, если частота равна 0,5 Гц, а амплитуда 80 см.

Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

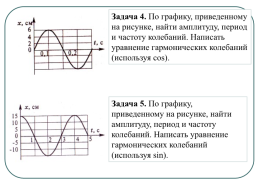
Задача 4. По графику, приведенному на рисунке, найти амплитуду, период и частоту колебаний. Написать уравнение гармонических колебаний (используя cos).
Задача 5. По графику, приведенному на рисунке, найти амплитуду, период и частоту колебаний. Написать уравнение гармонических колебаний (используя sin).

Домашнее задание
§22, 23, 24 прочитать, ответить на вопросы Упр.3(4,5), 417, 423

Использованные материалы
При создании презентации использовались иллюстрации «Механические колебательные системы» «Графики координаты x (t), скорости υ (t) и ускорения a (t) тела, совершающего гармонические колебания» (http://physics.ru/courses/op25part1/content/chapter2/section/paragraph1/theory.html )