Презентация - Первообразная

МОАУ СОШ с. Великокнязевки
ПЕРВООБРАЗНАЯ
Учитель математики I квалификационной категории Авраменко О.И.

Три пути ведут к знанию: путь размышления – это путь самый благородный путь подражания – это путь самый лёгкий путь опыта – это путь самый горький. Конфуций

Вычислите производные следующих функций:

Задача
При обработке на станке деталь нагреть до 1200. Измерения полагается производить при 200. Скорость охлаждения детали пропорциональна разности температур детали и воздуха в цехе. Сколько же нужно ждать? Здесь T(t) – температура детали, T/(t) = k(T-180)/- скорость её охлаждения. Ставится вопрос: зная производную некоторой функции, мы должны найти саму функцию. Как это сделать?

Заполнить пропущенные места в скобках
(…)/ = 2х (…)/ = 0 (…)/ = 4х3 (…)/ = 25

ПЕРВООБРАЗНАЯ
Цель: Определить понятие первообразной Задачи: 1. Научиться вычислять первообразную функции по ее производной. 2. Составить алгоритм нахождения первообразной. 3. Применить полученные знания при выполнении заданий

Физический смысл первообразной
нагрев
охлаждение

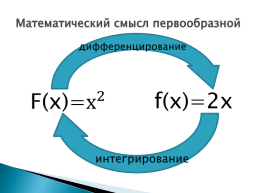
Математический смысл первообразной
дифференцирование
f(x)=2х
интегрирование

История интеграла

Производная – «производит» на свет новую функцию, первообразная - первичный образ. Определение
Функция F(x) называется первообразной для функции f(x) , если F/(x) = f(x) на заданном промежутке.

а) Проверить, что функция F(x) есть первообразная для f(x):
5) F(x) =10x10 f(x)=200x19

Пример нахождения первообразной

1) f(x)= x3 2) f(x) = x2 3) f(x) = x

Алгоритм
Подобрать функцию F(x) Найти её производную F/(x) Сравнить полученную производную F/(x) с данной функцией f(x) Если они совпадают, то задача решена, если нет, то вернуться к пункту 1).

Задание: Пользуясь данным алгоритмом, найти первообразные для следующих функций
f(x) = 1 f(x) = x3 f(x) = 0,25 f(x) = 5x f(x) = 6/x f(x) = 7x8 f(x) = 14x10 f(x) = 20x3

«Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию». Ян Амос Коменский

Рефлексия

Домашнее задание:
Глава 5 параграф 54. Первообразная № 983(2), 984(2)
Спасибо за урок!