Презентация - Текстовые задачи. Подготовка к ОГЭ
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 82%
- Слайдов: 34
- Просмотров: 1196
- Скачиваний: 100
- Размер: 0.98 MB
- Класс: 11
- Формат: ppt / pptx
Примеры похожих презентаций
 Готовимся к ОГЭ - Текстовые задачи на проценты и смеси (2 часть)
Готовимся к ОГЭ - Текстовые задачи на проценты и смеси (2 часть) Создание сборника задач по физике для подготовки к ОГЭ
Создание сборника задач по физике для подготовки к ОГЭ Подготовка к написанию сочинения на ОГЭ – 2020 по русскому языку (задания 9.1, 9.2, 9.3)
Подготовка к написанию сочинения на ОГЭ – 2020 по русскому языку (задания 9.1, 9.2, 9.3) Решение задач ОГЭ «Модуль геометрия» Часть 2
Решение задач ОГЭ «Модуль геометрия» Часть 2 Подготовка к огэ по географии. Вопрос 5:"Отрасли хозяйства России"
Подготовка к огэ по географии. Вопрос 5:"Отрасли хозяйства России" Возможности использования социальных сетей и других интернет-ресурсов при подготовке к ОГЭ
Возможности использования социальных сетей и других интернет-ресурсов при подготовке к ОГЭ Решение текстовых логических задач
Решение текстовых логических задач
Слайды и текст этой онлайн презентации
Слайд 1

Текстовые задачи
Подготовка к ОГЭ
2019 год
Слайд 2

Всякая хорошо решённая математическая задача доставляет умственное наслаждение. Г. Гессе
Слайд 3

Текстовые задачи разделяются на разные виды: по содержанию-на движение,работу,проценты,смеси и сплавы, по методам решения- арифметические, алгебраические(уравн),геометрические, комбинированные.
В прототипах самая большая группа задач- задачи на движение: Движение по прямой В одном направлении; Встречное; В разных направлениях; Движение по воде Движение по кругу Нахождение средней скорости Движение с учётом длины объекта
В прототипах самая большая группа задач- задачи на движение: Движение по прямой В одном направлении; Встречное; В разных направлениях; Движение по воде Движение по кругу Нахождение средней скорости Движение с учётом длины объекта
Слайд 4

Задачи на движение
Все задачи решаются по формуле S =vt либо используются формулы v=S/t, t=S/v В качестве переменной x удобно выбрать скорость. Уравнения составляются по одновременным событиям. Замечания: если время события задано, то удобнее составлять уравнение на путь; если уравнений меньше, чем неизвестных, то нужно ввести в систему искомую величину.
Все задачи решаются по формуле S =vt либо используются формулы v=S/t, t=S/v В качестве переменной x удобно выбрать скорость. Уравнения составляются по одновременным событиям. Замечания: если время события задано, то удобнее составлять уравнение на путь; если уравнений меньше, чем неизвестных, то нужно ввести в систему искомую величину.
Слайд 5

При решении задач на движение принимают допущения
движение считается равномерным; изменение направления движения считаются происходящими мгновенно; если два тела начинают движение одновременно, то до встречи каждое тело затрачивает одинаковое время; если тела выходят в разное время, то до встречи из них затрачивает время больше то, которое выходит раньше; в природе скорость расстояние и время положительны.
движение считается равномерным; изменение направления движения считаются происходящими мгновенно; если два тела начинают движение одновременно, то до встречи каждое тело затрачивает одинаковое время; если тела выходят в разное время, то до встречи из них затрачивает время больше то, которое выходит раньше; в природе скорость расстояние и время положительны.
Слайд 6

Что нужно помнить
Для успешного решения задач на движение нужно твердо держать в голове формулу-ключ, которая связывает путь (расстояние) , скорость и время : s=v·t Для удобства запоминания создадим свой «дорожный знак», который поможет нам найти любой из трех компонентов S – пройденный путь или расстояние, V – скорость, t - время
Для успешного решения задач на движение нужно твердо держать в голове формулу-ключ, которая связывает путь (расстояние) , скорость и время : s=v·t Для удобства запоминания создадим свой «дорожный знак», который поможет нам найти любой из трех компонентов S – пройденный путь или расстояние, V – скорость, t - время
Слайд 7

При решении задач необходимо:
согласовать единицы измерения скорости, пути и времени; если одно тело, движется со скоростью v1, догоняет другое, движущегося со скоростью v2 и находящегося от него на расстояние s, то скорость приближения равно v2 - v1,, а время t1, затраченное на то, чтобы догнать будет равно t1=s если тела движутся навстречу (при тех же параметрах), то скорость сближения будет равна v1+v2, встретиться же они через t2=s В случае, когда идет сравнение времени, затраченных на путь различными телами, для правильности уравнения связи этих времен надо посмотреть, какая из величин больше. При составлении уравнения, связывающего эти величины, необходимо ко второй прибавить или от первой отнять положительную величину.
согласовать единицы измерения скорости, пути и времени; если одно тело, движется со скоростью v1, догоняет другое, движущегося со скоростью v2 и находящегося от него на расстояние s, то скорость приближения равно v2 - v1,, а время t1, затраченное на то, чтобы догнать будет равно t1=s если тела движутся навстречу (при тех же параметрах), то скорость сближения будет равна v1+v2, встретиться же они через t2=s В случае, когда идет сравнение времени, затраченных на путь различными телами, для правильности уравнения связи этих времен надо посмотреть, какая из величин больше. При составлении уравнения, связывающего эти величины, необходимо ко второй прибавить или от первой отнять положительную величину.
Слайд 8

Интернет-ресурсы для подготовки к ОГЭ по математике
http://www.fipi.ru — портал информационной поддержки мониторинга качества образования, здесь можно найти Федеральный открытый банк заданий, а также демоверсии заданий ОГЭ и ГВЭ по всем предметам https://oge.sdamgia.ru — образовательный портал для подготовки к ОГЭ и ГВЭ по 14 предметам! Онлайн тесты и подробное пояснение к задачам и вопросам http://www.examen.ru — Все о ГИА и ЕГЭ. Онлайн тестирование http://alexlarin.net – образовательный портал для подготовки к ОГЭ по математике. Онлайн- тестирование. Сборники заданий второй части. http://www.yaklass.ru – образовательный портал для учащихся 1-11 классов, где можно повторить весь необходимый теоретический материал, а также пройти онлайн - тестирование.
http://www.fipi.ru — портал информационной поддержки мониторинга качества образования, здесь можно найти Федеральный открытый банк заданий, а также демоверсии заданий ОГЭ и ГВЭ по всем предметам https://oge.sdamgia.ru — образовательный портал для подготовки к ОГЭ и ГВЭ по 14 предметам! Онлайн тесты и подробное пояснение к задачам и вопросам http://www.examen.ru — Все о ГИА и ЕГЭ. Онлайн тестирование http://alexlarin.net – образовательный портал для подготовки к ОГЭ по математике. Онлайн- тестирование. Сборники заданий второй части. http://www.yaklass.ru – образовательный портал для учащихся 1-11 классов, где можно повторить весь необходимый теоретический материал, а также пройти онлайн - тестирование.
Слайд 9

Практическая часть проекта
Слайд 10

Алгоритм решения задач
Введи переменную х. Составь таблицу по данным задачи. Составь уравнение по условию задачи. Реши уравнение и проверь корни по условию задачи. Прочитай вопрос к задаче и дай на него ответ.
Введи переменную х. Составь таблицу по данным задачи. Составь уравнение по условию задачи. Реши уравнение и проверь корни по условию задачи. Прочитай вопрос к задаче и дай на него ответ.
Слайд 11

Движение по прямой из одного пункта в другой №1. Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 4 часа позже автомобилиста. Ответ дайте в км/ч. Решение:
.S (км).V (км/ч).t (ч)
Автомобилист...
Велосипедист...
х+40
х
50х + 4х(х+40) = 50(х+40) 50х+4х² +160х = 50х+2000 4х² +160х – 2000 = 0 х² +40х – 500 = 0 D = 3600; х₁ =10, х2 = - 50 Скорость не может быть отрицательной, следовательно скорость велосипедиста равна 10 км/ч. Ответ: 10
.S (км).V (км/ч).t (ч)
Автомобилист...
Велосипедист...
х+40
х
50х + 4х(х+40) = 50(х+40) 50х+4х² +160х = 50х+2000 4х² +160х – 2000 = 0 х² +40х – 500 = 0 D = 3600; х₁ =10, х2 = - 50 Скорость не может быть отрицательной, следовательно скорость велосипедиста равна 10 км/ч. Ответ: 10
Слайд 12
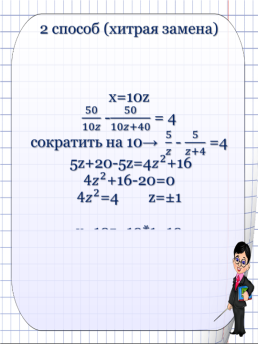
Слайд 13

№ 2 Самара,Кинель и Оренбург расположены на прямой автодороге, г.Кинель расположен между Самарой и Оренбургом. Из Самары в Оренбург выехал автомобиль, и одновременно с ним из Кинеля в Оренбург выехал второй автомобиль. Через какое время первый автомобиль догонит второй, если скорость первого на 15 км/час больше скорости второго, а расстояние между Самарой и Кинелём равно 45 км.
С х+15 К О 45 км Скорость сближения- разность скоростей (х+15-х= 15 км/ч) За какое время они сблизятся? 45: 15=3 часа Ответ: 3 ч.
Х км/ч
С х+15 К О 45 км Скорость сближения- разность скоростей (х+15-х= 15 км/ч) За какое время они сблизятся? 45: 15=3 часа Ответ: 3 ч.
Х км/ч
Слайд 14

№ 3 Первый велосипедист выехал из посёлка по шоссе со скоростью 21 км/ч, через час после него со скоростью 15 км/ч из того же посёлка в том же направлении выехал второй, а ещё через час после этого- третий.Найти скорость третьего велосипедиста,если он сначала догнал второго,а через 9 часов после этого догнал первого.
15 км 2 1 42 км 1-й ехал 2 ч s=21*2=42 км 2-й ехал 1 ч s=1*15=15км 3-й выехал
.S.V вдог.t
3-й и 2-й.15.х-15.
3-й и 1-й.42.х-21.
15 км 2 1 42 км 1-й ехал 2 ч s=21*2=42 км 2-й ехал 1 ч s=1*15=15км 3-й выехал
.S.V вдог.t
3-й и 2-й.15.х-15.
3-й и 1-й.42.х-21.
Слайд 15

Слайд 16

№ 3.Из городов А и В навстречу друг другу выехал мотоциклист и велосипедист. Мотоциклист приехал в В на 2 часа раньше,чем велосипедист приехал в А, а встретились они через 45 мин после выезда. Скольско часов затратил на путь из В в А велосипедист?
Слайд 17

Слайд 18

№ 4. Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя 1 час, когда одному из них оставалось 8 км до окончания 1 круга ,ему сообщили, что другой бегун прошёл 1-й круг 3 мин назад. Найти скорость первого бегуна, если известно,что она на 9 км/ч меньше скорости второго от А до С -3 мин
3 мин
8 км
А
ВА= 8 км
С
В
.V.S.t
1-й бегун.х.х.1
2-й бегун.х+9.х+9.1
3 мин
8 км
А
ВА= 8 км
С
В
.V.S.t
1-й бегун.х.х.1
2-й бегун.х+9.х+9.1
Слайд 19
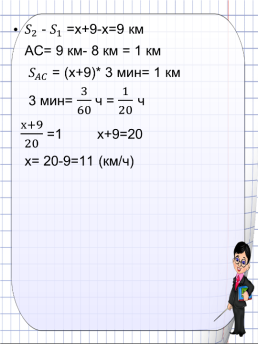
Слайд 20

Нахождение средней скорости
№ 5. Первую половину трассы автомобиль проехал со скоростью 56 км/ч, а вторую — со скоростью 84 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
№ 5. Первую половину трассы автомобиль проехал со скоростью 56 км/ч, а вторую — со скоростью 84 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Слайд 21

Средняя скорость на 3-х участках движения
№ 6. Первые 300 км автомобиль ехал со скоростью 60 км/ч, следующие 300 км — со скоростью 100 км/ч, а последние 300 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Решение. Средняя скорость — это все пройденное расстояние, разделённое на все затраченное время движения. Первый отрезок пути автомобиль проехал за 300/6 = 5 часов, второй — за 300/100 = 3 часа, третий — за 300/75 = 4 часа. Средняя скорость автомобиля на протяжении всего пути составила Ответ: 75км/ч.
№ 6. Первые 300 км автомобиль ехал со скоростью 60 км/ч, следующие 300 км — со скоростью 100 км/ч, а последние 300 км — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Решение. Средняя скорость — это все пройденное расстояние, разделённое на все затраченное время движения. Первый отрезок пути автомобиль проехал за 300/6 = 5 часов, второй — за 300/100 = 3 часа, третий — за 300/75 = 4 часа. Средняя скорость автомобиля на протяжении всего пути составила Ответ: 75км/ч.
Слайд 22

Движение с учётом длины объекта
Слайд 23

№ 9. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 70 км/ч и 30 км/ч. Длина товарного поезда равна 1400 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 3 минутам.
70-30=40(км/ч) – скорость сближения поездов 40 км/ч = 40 ·1000:60 м/мин = 2000/3 м/мин. 3·2000/3= 2000(м) – проедет пассажирский поезд за 3 минуты, это расстояние равно сумме длин поездов. 2000 – 1400 = 600(м) – длина пассажирского поезда Ответ: 600 метров.
70-30=40(км/ч) – скорость сближения поездов 40 км/ч = 40 ·1000:60 м/мин = 2000/3 м/мин. 3·2000/3= 2000(м) – проедет пассажирский поезд за 3 минуты, это расстояние равно сумме длин поездов. 2000 – 1400 = 600(м) – длина пассажирского поезда Ответ: 600 метров.
Слайд 24

№ 10. Поезд, двигаясь равномерно со скоростью 54 км/ч, проезжает мимо идущего параллельно путям со скоростью 6 км/ч навстречу ему пешехода за 30 секунд. Найдите длину поезда в метрах.
Решение: 54+6=60 (км/ч) скорость сближения 60 км/ч = 60·1000:60 м/мин 30 сек. = 0,5 мин 1000·0,5 = 500 (м) длина поезда. Ответ: 500 м.
Решение: 54+6=60 (км/ч) скорость сближения 60 км/ч = 60·1000:60 м/мин 30 сек. = 0,5 мин 1000·0,5 = 500 (м) длина поезда. Ответ: 500 м.
Слайд 25

Разные задачи: Человек идет по движущемуся эскалатору и спускается за 72 с. Стоя на ступеньке движущегося эскалатора – за 136 с. За сколько с спустится пассажир, если он идет по неподвижному эскалатору?
Запишем все известные данные: S = tч ⋅ Vч – чел. спускается по неподвижному эск. S = 136 ⋅ Vэ – чел.стоит на ступеньке движущегося эск S = 72 ⋅ (Vч + Vэ) – чел. идет по движущемуся эск. Приравняем второе и третье равенство (так как расстояние одинаково) и выразим скорость человека: 72 ⋅ (Vч + Vэ) = 136 ⋅ Vэ 72 Vч + 72Vэ = 136Vэ 72Vч = (136 – 72)Vэ 72Vч = 64Vэ Vч = 8/9 ⋅ Vэ Теперь достаточно приравнять первое и второе равенство, предварительно заменив в первом равенстве скорость человека на полученную, чтобы получить время спуска человека по неподвижному эскалатору: tч ⋅ 8/9 ⋅ Vэ = 136 ⋅ Vэ tч = 136 ⋅ Vэ / (8/9 ⋅ Vэ) tч = 153 c Ответ: 153
Запишем все известные данные: S = tч ⋅ Vч – чел. спускается по неподвижному эск. S = 136 ⋅ Vэ – чел.стоит на ступеньке движущегося эск S = 72 ⋅ (Vч + Vэ) – чел. идет по движущемуся эск. Приравняем второе и третье равенство (так как расстояние одинаково) и выразим скорость человека: 72 ⋅ (Vч + Vэ) = 136 ⋅ Vэ 72 Vч + 72Vэ = 136Vэ 72Vч = (136 – 72)Vэ 72Vч = 64Vэ Vч = 8/9 ⋅ Vэ Теперь достаточно приравнять первое и второе равенство, предварительно заменив в первом равенстве скорость человека на полученную, чтобы получить время спуска человека по неподвижному эскалатору: tч ⋅ 8/9 ⋅ Vэ = 136 ⋅ Vэ tч = 136 ⋅ Vэ / (8/9 ⋅ Vэ) tч = 153 c Ответ: 153
Слайд 26

Алгоритм решения задач при движении по воде
Введи переменную х. Составь таблицу по данным задачи с учетом движения по течению и против течения. Составь уравнение по условию задачи. Реши уравнение и проверь корни по условию задачи. Прочитай вопрос к задаче и дай на него ответ.
Введи переменную х. Составь таблицу по данным задачи с учетом движения по течению и против течения. Составь уравнение по условию задачи. Реши уравнение и проверь корни по условию задачи. Прочитай вопрос к задаче и дай на него ответ.
Слайд 27

№ 11. Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.
Решение: Пусть х км/ч - собственная скорость лодки(в неподвижной воде), тогда (х+4)км/ч – скорость лодки по течению реки, (х-4)км/ч – скорость лодки против течения реки. 77/(х-4)ч – время лодки против течения реки, 77/(х-4)ч – время по течению реки, на 2ч меньше Составим уравнение 77/(х-4) – 77(х+4) = 2 и решим его. х=18 Значит, собственная скорость лодки 18 км/ч. Ответ: 18 КМ/Ч
Решение: Пусть х км/ч - собственная скорость лодки(в неподвижной воде), тогда (х+4)км/ч – скорость лодки по течению реки, (х-4)км/ч – скорость лодки против течения реки. 77/(х-4)ч – время лодки против течения реки, 77/(х-4)ч – время по течению реки, на 2ч меньше Составим уравнение 77/(х-4) – 77(х+4) = 2 и решим его. х=18 Значит, собственная скорость лодки 18 км/ч. Ответ: 18 КМ/Ч
Слайд 28

№ 12 Моторная лодка спустилась вниз по течению реки на 18 км и вернулась обратно,затратив на весь путь 1 ч 45 мин. Найти собственную скорость лодки,если известно,что 6 км по течению реки лодка проплывает на 5 мин быстрее, чем против течения.
Пусть х- собст.скорость лодки у- скорость течения
.S.V.t
По течен..18.х+у.
Против течен..18.х-у.
.S.V.t
По течен..6.х+у.
Против течен..6.х-у.
Пусть х- собст.скорость лодки у- скорость течения
.S.V.t
По течен..18.х+у.
Против течен..18.х-у.
.S.V.t
По течен..6.х+у.
Против течен..6.х-у.
Слайд 29

Слайд 30

Памятка при решении задач на движение
1) Путь = скорость · время 2) При движении по реке: Скорость по течению = собственная скорость транспорта + скорость течения реки Скорость против течения = собственная скорость транспорта - скорость течения реки
1) Путь = скорость · время 2) При движении по реке: Скорость по течению = собственная скорость транспорта + скорость течения реки Скорость против течения = собственная скорость транспорта - скорость течения реки
Слайд 31

Задачи на проценты, работу, сплавы, смеси.
88%
30%
вода
вода
- Вода =
12% сухого
70% сухого
88%
30%
вода
вода
- Вода =
12% сухого
70% сухого
Слайд 32

№ 14 Первая труба пропускает на 10 л воды в мин. меньше,чем вторая труба. Сколько литров воды в мин. пропускает первая труба,если резервуар объёмом 60 л. Она заполняет на 3 мин. раньше чем вторая
А
р
t
.A.p.t
1-я труба.60.х.
2-я труба.60.Х+10.
Х=10z
А
р
t
.A.p.t
1-я труба.60.х.
2-я труба.60.Х+10.
Х=10z
Слайд 33

Слайд 34

Задачи на сплавы,смеси. № 15 Первый сплав содержит 5% меди,второй 13% меди. Масса второго сплава больше массы первого на 4 кг. Из этих двух сплавов получили третий, содержащий 10% меди. Найти массу третьего.
5х+13(х+4)=10(2х+4) 20х+40-18х=52 2х=12 х=6 6+6+4=16(кг) Ответ: 16 кг
5%
13%
10%
х
Х+х+4
Х+4
5х+13(х+4)=10(2х+4) 20х+40-18х=52 2х=12 х=6 6+6+4=16(кг) Ответ: 16 кг
5%
13%
10%
х
Х+х+4
Х+4
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
