Презентация - Готовимся к ОГЭ - Текстовые задачи на проценты и смеси (2 часть)

ГОТОВИМСЯ к ОГЭ 2017
ТЕКСТОВЫЕ ЗАДАЧИ на проценты и смеси (2 часть)

Девиз:
« Не делай никогда того, чего не знаешь, но научись всему, что следует знать» Пифагор

Кроссворд: 1.Сотая часть числа называется … 2.Частное двух чисел называют … 3.Верное равенство двух отношений называют … 4.В химии определение этого понятия звучало бы так: гомогенная смесь, образованная не менее чем двумя компонентами … Один из которых называется растворителем, а другой растворимым веществом. 5.Отношение массы растворимого вещества к массе раствора называют массовой долей вещества в растворе или …
1
2
3
4
5
 
о

Задание 1. Установите соответствие
7 % 16% 113% 0,4% 25%

0,004 0,25 0,07 0,16 1,13
4

100% = 1 10% = 1/10 50% = ½ 5% = 1/20 25% = 1/4 200% = 2
1% = 1/100
Сокращенные процентные соотношения

Основные задачи на проценты
р % = 0,01р = р/100 1. Нахождение процентов данного числа. Чтобы найти р % от а, надо а·0,01р 2. Нахождение числа по его процентам. Если известно, что р% числа равно b, то а = b: 0,01р 3. Нахождение процентного отношения чисел. Чтобы найти процентное отношение чисел, надо отношение этих чисел умножить на 100% а/b ·100

Задание 2. Произвести расчеты
1. Найти 25% от 56 14
2. Сколько % составит 30 от 75? 40
Какое число, увеличенное на 13% составит 339? 300
3.Найдите число, 20% которого равны 12 60
5. В избирательном округе нашего посёлка 1005 человек. В голосовании приняло 40%.Сколько человек голосовало? 402
Банк начисляет на вклад ежегодно 8% от вложенной суммы. Сколько рублей будет начислено через год на вклад в 5000 р.? 400 р.

Задача 1.

При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не менее 300 рублей. Какую минимальную сумму она должна положить в приёмное устройство данного терминала?
Решение: 300 · 0,05= 15 (р) – комиссия 300+15 = 315 (р) – можно положить 320 р. надо положить на счёт Ответ:320р.

Задача 2.
На покупку планшета взяли кредит 20000 р. на 1 год под 16 % годовых . Вычислите, сколько денег необходимо вернуть банку? Какова ежемесячная сумма выплат?
Решение : 20000 · 0,16 = 3200(р) составляют проценты 20000 + 3200 = 23200 (р) вся сумма выплат 23200:12= 1933(р)- за 1 месяц Ответ:1933р.

Задача 3.
Мобильный телефон стоил 5000 рублей. Через некоторое время цену на эту модель снизили до 3000 рублей. На сколько процентов была снижена цена?
Решение: 5000 – 3000 = 2000(р) – на столько снижена цена на телефон (2000: 5000) · 100% = (2:5) · 100% = 0,4 · 100 = =40 % на столько снижена цена Ответ: на 40 %.

Задачи на смеси и сплавы
Наименова-ние веществ, растворов, смесей, сплавов % содержание вещества (доля содержания вещества) Масса раствора (смеси, сплава) Масса вещества

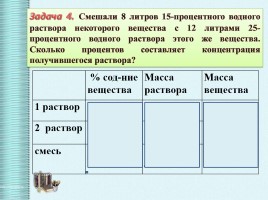
Задача 4. Смешали 8 литров 15-процентного водного раствора некоторого вещества с 12 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
% сод-ние вещества Масса раствора Масса вещества
1 раствор 15% = 0,15 8 л 8 ∙0,15
2 раствор 25% = 0,25 12 л 12 ∙ 0,25
смесь X 8 + 12 = 20 л 20 x

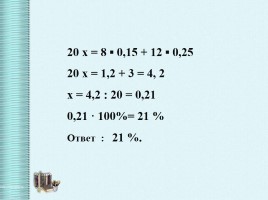
20 x = 8 ▪ 0,15 + 12 ▪ 0,25 20 x = 1,2 + 3 = 4, 2 x = 4,2 : 20 = 0,21 0,21 · 100%= 21 % Ответ : 21 %.

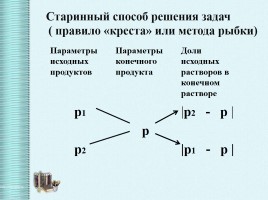
Параметры исходных продуктов Параметры конечного продукта Доли исходных растворов в конечном растворе
p1 |p2 - p |
p
p2 |p1 - p |
Старинный способ решения задач ( правило «креста» или метода рыбки)

Задача 5. Один раствор содержит 20 % соли, а второй – 70 %. Сколько граммов первого и второго раствора нужно взять, чтобы получить 100 г 50% раствора.
.
100 г смеси составляют 20 + 30 = 50(%) 100 : ( 20 + 30 ) = 2(г) - на 1%. 2 ∙ 20 = 40(г) – 20% раствора 2 ∙ 30 = 60(г) – 70 % раствора Ответ: 40 г- 20 % раствора; 60 г- 70 % раствора
Применим «метод рыбки». Составим схему:
100

Задача 6. Первый сплав содержит 10 % меди, второй - 25 % меди. Из этих двух сплавов получили третий сплав массой 3 кг, содержащий 20 % меди. Какое количество каждого сплава было использовано?
Решить с помощью системы Решить с помощью уравнения Решить с помощью «метода рыбки»

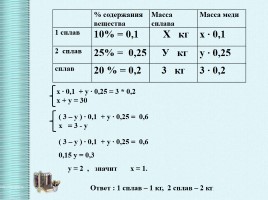
% содержания вещества Масса сплава Масса меди
1 сплав 10% = 0,1 Х кг х ∙ 0,1
2 сплав 25% = 0,25 У кг у ∙ 0,25
сплав 20 % = 0,2 3 кг 3 ∙ 0,2

х ∙ 0,1 + у ∙ 0,25 = 3 * 0,2 х + у = 30
( 3 – у ) ∙ 0,1 + у ∙ 0,25 = 0,6 0,15 у = 0,3 у = 2 , значит х = 1. Ответ : 1 сплав – 1 кг, 2 сплав – 2 кг.
( 3 – у ) ∙ 0,1 + у ∙ 0,25 = 0,6 х = 3 - у

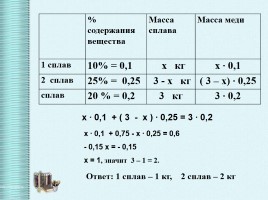
% содержания вещества Масса сплава Масса меди
1 сплав 10% = 0,1 х кг х ∙ 0,1
2 сплав 25% = 0,25 3 - х кг ( 3 – х) ∙ 0,25
сплав 20 % = 0,2 3 кг 3 ∙ 0,2

х ∙ 0,1 + ( 3 - х ) ∙ 0,25 = 3 ∙ 0,2
х ∙ 0,1 + 0,75 - х ∙ 0,25 = 0,6 - 0,15 х = - 0,15 х = 1, значит 3 – 1 = 2.
Ответ: 1 сплав – 1 кг, 2 сплав – 2 кг

3 способ: ( «метод рыбки»)
5 + 10 = 15 (%) в 3 кг 3 : 15 = 0,2 кг – в 1% На 5% – 0,2 ∙ 5 = 1(кг) На 10% - 0, 2∙10 = 2(кг) Ответ : 1 сплав – 1 кг, 2 сплав – 2 кг.
3кг

4 способ По формуле m1·p1 +m2·p2 +…+ · =p(m1+ m2 + … + ), где m1, m2 , - массы растворов, Р –процентное содержание нового раствора, p1 и p2, - процентное содержание растворов.

Решение: Пусть масса первого раствора Х кг, масса второго раствора у кг. Используя формулу составим систему уравнений.
10х +25у =20·3 Х + у =3
10х +25у =60 Х =3-у
10(3-х)+25у=60 15у=30 У=2 Х=3-2=1 Ответ:1 сплав – 1 кг, 2 сплав – 2 кг.

При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получился раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы?
Решение. 20%=1/5 30%=3/10 50%=1/2 Составим уравнение: 1/5 ·х + 1/2·у = 3/10·(х + у)
х
у
х + у
получили

Решаем уравнение: 1/5·х + 1/2·у = 3/10·(х + у) 1/5·х + 1/2·у = 3/10·х + 3/10·у 1/5·х - 3/10·х = 3/10·у - 1/2·у х (1/5 - 3/10) = у (3/10 - 1/2 ) Надо найти отношение первого и второго растворов, т.е. как х : у, поэтому уравнение делим на у: Получаем: х/у ·(-1/10) = -1/5 х/у = (-1/5) : (-1/10) = -1/5 · (-10/1) = + 2 Значит х : у = 2:1 Ответ: 2:1

Задача
сложная
интересная
находить
простая
записывать
решать
?

Сегодня на уроке я повторил Сегодня на уроке я узнал Сегодня на уроке я научился

Рефлексия
– не допустил ни одной ошибки, доволен собой; – допустил неточность; – надо постараться и успех будет!

Оцени по пятибальной шкале: "МЫ"........... "Я"............ "Наше дело"...............

Спасибо за урок