Презентация - Степенная функция в зависимости от показателя

Степенная функция в зависимости от показателя

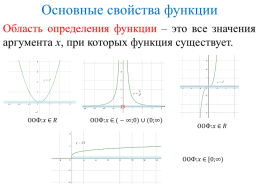
Основные свойства функции
Область определения функции – это все значения аргумента х, при которых функция существует.

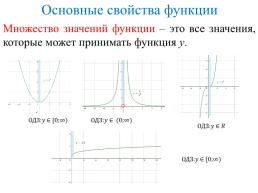
Основные свойства функции
Множество значений функции – это все значения, которые может принимать функция у.

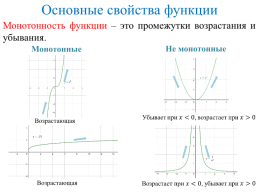
Основные свойства функции
Монотонность функции – это промежутки возрастания и убывания.
Не монотонные
Монотонные
Убывает при ,
возрастает при
Возрастающая
Возрастающая
убывает при
Возрастает при ,

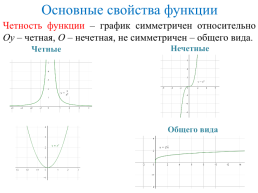
Основные свойства функции
Четность функции – график симметричен относительно Оу – четная, О – нечетная, не симметричен – общего вида.
Нечетные
Четные
Общего вида

Основные свойства функции
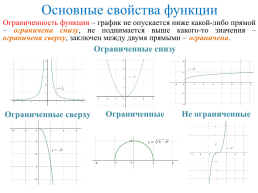
Ограниченность функции – график не опускается ниже какой-либо прямой – ограничена снизу, не поднимается выше какого-то значения – ограничена сверху, заключен между двумя прямыми – ограничена.
Ограниченные снизу
Не ограниченные
Ограниченные
Ограниченные сверху

Основные свойства функции
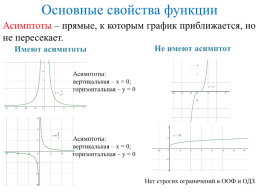
Асимптоты – прямые, к которым график приближается, но не пересекает.
Не имеют асимптот
Имеют асимптоты
Асимптоты: вертикальная – х = 0; горизонтальная – у = 0
Асимптоты: вертикальная – х = 0; горизонтальная – у = 0
Нет строгих ограничений в ООФ и ОДЗ

Основные свойства функции
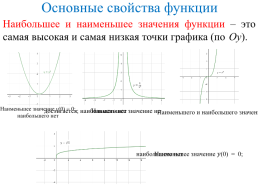
Наибольшее и наименьшее значения функции – это самая высокая и самая низкая точки графика (по Оу).
Наименьшее значение y(0) = 0; наибольшего нет

Графики и свойства степенных функций в зависимости от показателя
Функция называется степенной. Здесь р – заданное действительное число (рассмотренные ранее функции являются степенными). Свойства и графики степенной функции существенно отличаются в зависимости от показателя степени.
Степенными считаются также дробные функции иррациональные функции (с корнями)
Схематично графики функций в зависимости от того, какой показатель находится в степени, будут иметь один и тот же вид.

1) Показатель степени р = 0
Свойства: 1) ООФ: (любое действительное число). На графике видно, что функция простирается как влево, так и вправо по оси ОХ. 2) ОДЗ: . Так как функция при любых значениях х равна а. 3) Четная, т. к. . 4) Постоянная (не возрастает и не убывает) 5) Ограничена, так как принимает только значения равные а. 6) Асимптот не имеет, так как никаких ограничений в ООФ и ОДЗ нет. 7) Не принимает ни наибольшего, ни наименьшего значений.
Графиком функции является прямая, параллельная оси абсцисс. Например, у = 1, у = 3, у = -5 и т.д.

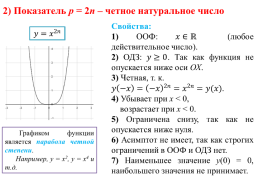
2) Показатель р = 2n – четное натуральное число
Свойства: 1) ООФ: (любое действительное число). 2) ОДЗ: . Так как функция не опускается ниже оси ОХ. 3) Четная, т. к. . 4) Убывает при x < 0, возрастает при x < 0. 5) Ограничена снизу, так как не опускается ниже нуля. 6) Асимптот не имеет, так как строгих ограничений в ООФ и ОДЗ нет. 7) Наименьшее значение у(0) = 0, наибольшего значения не принимает.
Графиком функции является парабола четной степени. Например, у = х2, у = х4 и т.д.

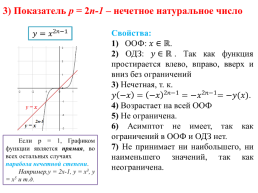
3) Показатель р = 2n-1 – нечетное натуральное число
Свойства: 1) ООФ: . 2) ОДЗ: . Так как функция простирается влево, вправо, вверх и вниз без ограничений 3) Нечетная, т. к. . 4) Возрастает на всей ООФ 5) Не ограничена. 6) Асимптот не имеет, так как ограничений в ООФ и ОДЗ нет. 7) Не принимает ни наибольшего, ни наименьшего значений, так как неограничена.
Если р = 1, Графиком функции является прямая, во всех остальных случаях парабола нечетной степени. Например,у = 2х-1, у = х3, у = х5 и т.д.

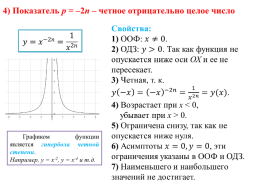
4) Показатель р = –2n – четное отрицательно целое число
Свойства: 1) ООФ: . 2) ОДЗ: . Так как функция не опускается ниже оси ОХ и ее не пересекает. 3) Четная, т. к. . 4) Возрастает при x < 0, убывает при x > 0. 5) Ограничена снизу, так как не опускается ниже нуля. 6) Асимптоты , эти ограничения указаны в ООФ и ОДЗ. 7) Наименьшего и наибольшего значений не достигает.
Графиком функции является гипербола четной степени. Например, у = х-2, у = х-4 и т.д.

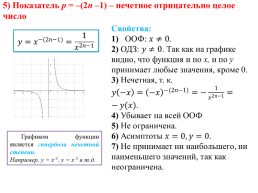
5) Показатель р = –(2n –1) – нечетное отрицательно целое число
Свойства: 1) ООФ: . 2) ОДЗ: . Так как на графике видно, что функция и по х, и по у принимает любые значения, кроме 0. 3) Нечетная, т. к. . 4) Убывает на всей ООФ 5) Не ограничена. 6) Асимптоты . 7) Не принимает ни наибольшего, ни наименьшего значений, так как неограничена.
Графиком функции является гипербола нечетной степени. Например, у = х-3, у = х-5 и т.д.

6) Показатель р – нецелое положительное число
Свойства: 1) ООФ: . 2) ОДЗ: . Так как на графике видно, что функция и по х, и по у принимает только неотрицательные значения. 3) Общего вида, т. к. не определено. 4) Возрастает на всей ООФ 5) Ограничена снизу. 6) Асимптот нет, так как строгих ограничений в ООФ и ОДЗ нет. 7) Наименьшее значение у(0) = 0, наибольшего значения не принимает.
Если p > 1, графиком функции является вертикальная ветвь параболы, если 0 < p < 1, горизонтальная ветвь параболы. Например, у = х5,3, у = х1/2 и т.д.

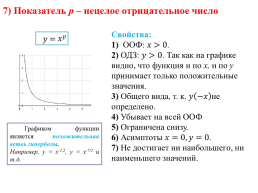
7) Показатель р – нецелое отрицательное число
Свойства: 1) ООФ: . 2) ОДЗ: . Так как на графике видно, что функция и по х, и по у принимает только положительные значения. 3) Общего вида, т. к. не определено. 4) Убывает на всей ООФ 5) Ограничена снизу. 6) Асимптоты . 7) Не достигает ни наибольшего, ни наименьшего значений.
Графиком функции является положительная ветвь гиперболы. Например, у = х-1,2, у = х-7/2 и т.д.

Задание для самостоятельной работы
Распределить данные функции по рассмотренным 7ми группам в зависимости от показателя. Для каждой группы построить схематичный график (по одному для каждой группы) и описать свойства.