Презентация - Показательная функция её применение в природе и технике

Показательная функция
её применение в природе и технике

Показательная функция. Функция вида у=ах ,где а-заданное число, а>0, а≠1, х-переменная, называется показательной.

Показательная функция. Функция вида у=ах ,где а-заданное число, а>0, а≠1, х-переменная, называется показательной.

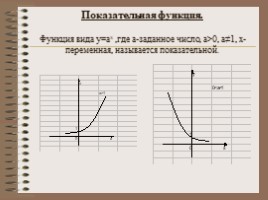
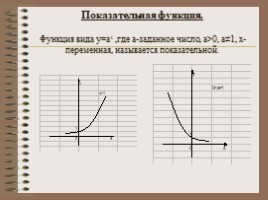
Показательная функция обладает следующими свойствами:
Д(у): множество R всех действительных чисел; Е(у):множество всех положительных чисел; Показательная функция у=ах является возрастающей на множестве всех действительных чисел,если а>1,и убывающей,если 0<а<1; Не является ни четной, ни нечетной; Не ограничена сверху,ограничена снизу; Не имеет ни наибольшего, ни наименьшего значения; Непрерывна; Если а>1 ,то функция выпукла вниз.

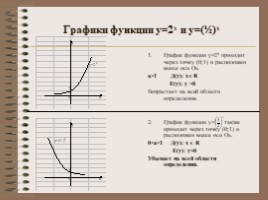
Графики функции у=2х и у=(½)х
График функции у=2х проходит через точку (0;1) и расположен выше оси Ох. а>1 Д(у): х є R Е(у): у >0 Возрастает на всей области определения. График функции у= также проходит через точку (0;1) и расположен выше оси Ох. 0<а<1 Д(у): х є R Е(у): у>0 Убывает на всей области определения.

Подумайте! Где может использоваться показательная функция?
Тема «Показательная функция» является основополагающей при изучении таких тем, как «Производная показательной функции», «Термодинамика», «Электромагнетизм», «Ядерная физика», «Колебания», используется для решения некоторых задач судовождения.

Наглядный бытовой пример!
Все, наверное, замечали, что если снять кипящий чайник с огня, то сначала он быстро остывает, а потом остывание идет гораздо медленнее. Дело в том, что скорость остывания пропорциональна разности между температурой чайника и температурой окружающей среды. Чем меньше становится эта разность, тем медленнее остывает чайник. Если сначала температура чайника равнялась Т0, а температура воздуха T1, то через t секунд температура Т чайника выразится формулой: T=(T1-T0)ekt+T1 где k - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которое в нем находится.

При падении тел в безвоздушном пространстве скорость их непрерывно возрастает
При падении тел в воздухе скорость падения тоже увеличивается, но не может превзойти определенной величины

Рассмотрим задачу о падении парашютиста. Если считать, что сила сопротивления воздуха пропорциональна скорости падения парашютиста, т.е. что F=kv , то через t секунд скорость падения будет равна: k(1-e ) где m - масса парашютиста. Через некоторый промежуток времени е станет очень маленьким числом, и падение станет почти равномерным. Коэффициент пропорциональности k зависит от размеров парашюта. Данная формула пригодна не только для изучения падения парашютиста, но и для изучения падения капли дождевой воды, пушинки и т.д.
mg
V=
кt m
кt m

Много трудных математических задач приходится решать в теории межпланетных путешествий. Одной из них является задача об определении массы топлива, необходимого для того, чтобы придать ракете нужную скорость v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости v0, с которой продукты горения вытекают из ракетного двигателя.

Если не учитывать сопротивление воздуха и притяжение Земли, то масса топлива определиться формулой: M=m(ev/v0-1) Например, для того чтобы ракете с массой 1,5 т придать скорость 8000 м/с, надо при скорости истечения газов 2000 м/с взять примерно 80 т топлива.
Формула К.Э.Циалковского

Применение в ядерной физике
Когда радиоактивное вещество распадется, его количество уменьшается. Через некоторое время остается половина первоначального количества вещества. Этот промежуток времени t0 называется периодом полураспада. Вообще через t лет масса m вещества будет равна: m=m0(1/2)t/t0, где m0 - первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество. Явление радиоактивного распада используется для определения возраста археологических находок, например, определен примерный возраст Земли, около 5,5 млрд. лет, для поддержания эталона времени.

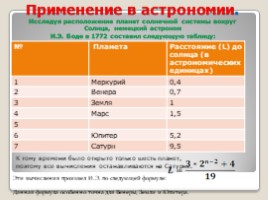
Применение в астрономии. Исследуя расположение планет солнечной системы вокруг Солнца, немецкий астроном И.Э. Боде в 1772 составил следующую таблицу:
№ Планета Расстояние (L) до солнца (в астрономических единицах)
1 Меркурий 0,4
2 Венера 0,7
3 Земля 1
4 Марс 1,5
5
6 Юпитер 5,2
7 Сатурн 9,5
К тому времени было открыто только шесть планет, поэтому все вычисления останавливаются на Сатурне.
Эти вычисления произвел И.Э. по следующей формуле: Данная формула особенно точна для Венеры, Земли и Юпитера.

Как известно, между Марсом и Юпитером планеты не существует, но если следовать таблице Боде, на данной орбите должно находиться какое-либо космическое тело. И действительно, после некоторых исследований учёными был открыт пояс астероидов. Это было воистину торжеством науки и триумфом математики!

Применение показательной функции в биологии

Применение показательной функции в биологии
В питательной среде бактерия кишечной палочки делится каждую минуту. Понятно, что общее число бактерий за каждую минуту удваивается. Если в начале процесса была одна бактерия, то через х минут их число (N) станет равной 2х , т.е. N(х) = 2х.

Применение в биологии
Процессы выравнивания  (именно так  называют процессы, изменяющиеся по законам показательной функции)  часто встречаются и в биологии. Например, при испуге в кровь внезапно выделяется адреналин, который потом разрушается, причем скорость разрушения примерно пропорциональна количеству этого вещества, еще остающемуся в крови. При диагностике почечных бо­лезней часто определяют способность почек выводить из крови радиоактивные изотопы, причем их количество в крови падает по показательному закону. Примером обратного процесса может служить восстановление концентрации гемоглобина в крови у донора или у раненого, потерявшего много крови. В этом случае по показательному закону убывает разность между нормальным содержанием гемоглобина и имеющимся количеством этого вещества. Как и при радиоактивном распаде, скорость распада или восстановления измеряется временем, в течение которого распадается (соответственно восстанавливается) половина вещества. Для адреналина этот период измеряется долями секунды, для веществ, выводимых почками, — минутами, а для   гемоглобина — днями.

По такому же принципу распространились завезённые в Австралию кролики, которые стали экологической катастрофой для этого уникального региона. Рост различных видов микроорганизмов и бактерий, дрожжей, ферментов все эти процессы подчиняются одному закону: N = N0ekt 
Закон органического размножения: при благоприятных условиях (отсутствие врагов, большое количество пищи) живые организмы размножались бы по закону показательной функции.  Например: одна комнатная муха может за лето произвести 8   1014 особей потомства. Их вес составил бы несколько миллионов тонн (а вес потомство пары мух превысил бы вес нашей планеты), они бы заняли огромное пространство, а если выстроить их в цепочку, то её длинна будет больше, чем расстояние от Земли до Солнца. Но так как, кроме мух существует множество других животных и растений, многие из которых являются естественными врагами мух их количество не достигает вышеуказанных значений.
Применение в биологии.

Рост народонаселения
. Изменение числа людей в стране на небольшом отрезке времени описывается формулой   , где  N0  - число людей  в момент времени t=0, N -число людей в момент времени t,  a k-константа.

Применение показательной функции в экономике.

Задача:
Ежемесячно на банковский вклад, равный S0 рублей начисляется р%. На сколько процентов возрастет банковский вклад за х месяцев?
Решение.

Задача:
Процент инфляции показывает, на сколько процентов (в среднем) выросли цены. 1) Выразите процент инфляции за х месяцев, если ежемесячно инфляция составляет 3%. 2) Вычислите с помощью калькулятора годовой процент инфляции.
Решение.

Вывод
Никогда ещё математика не была настолько всеобъемлющей и такой нужной людям наукой, как сегодня. О том, какой будет математика завтра, говорить трудно. Она развивается сейчас так стремительно, так часто делаются в ней новые открытия, что гадать о том, что будет, пожалуй, бесполезно. Одно можно сказать наверняка: завтра математика станет ещё могущественнее, ещё важнее и нужнее людям, чем сегодня.

Математика как наука основывается на разнообразие математических моделей, главной задачей которых является отображение реальных событий и явлений. Отсюда следует и главная цель математики с практической ее стороны - разработка таких моделей, которые смогли бы в достаточной мере объяснить исследуемое явление или объект.