Слайды и текст этой онлайн презентации
Слайд 1
Учительство - не труд, а отреченье,
Умение всего себя отдать,
Уйти на долгий подвиг и мученье,
И в этом видеть свет и благодать.
Учительство - когда в глазах холодных
Зажжется понимания заря,
И ты поймешь: старался не бесплодно
И знания разбрасывал не зря.
Слайд 2
Липлянская Татьяна Геннадьевна,
учитель математики МОБУ «СОШ №3»
город Ясный Оренбургская область
Слайд 4
Исследование функций с применением производной
Исследование функции на экстремумы;
Исследование функции на возрастание/ убывание;
Исследование функции на наибольшие и наименьшие значения на отрезке;
Исследование функции с помощью графика ее производной (чтение графика производной)
Слайд 5
Если f′(x)>0 в каждой точке интервала, то функция y=f(x) возрастает на этом интервале.
Если f′(x)<0 в каждой точке интервала, то функция y=f(x) убывает на этом интервале.
Исследование функции на возрастание (убывание)
f(x) дифференцируема на интервале (a;b)
Слайд 6
Признак максимума. Если функция f(x) – непрерывна в точке х0
Признак минимума. Если функция f(x) – непрерывна в точке х0
Исследование функции на экстремумы
Слайд 7
x
y
a
b
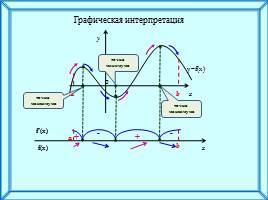
y=f(x)
точка
максимума
точка
максимума
точка
минимума
f(x)
f′(x)
a
b
+
+
-
-
Графическая интерпретация
0
x
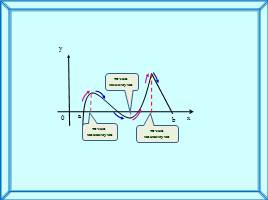
Слайд 8
точка
максимума
точка
минимума
точка максимума
Слайд 9
Алгоритм
1. Найти f ′ (x)
2. Найти стационарные (f′(x)=0) и критические точки (f′(x) не существует)
3. Определить знаки производной, выполнить графическую иллюстрацию.
1) y / = 3x2 – 48
2) y / = 3x2 – 48 = 3(x2 – 16) = 3(x – 4)(x + 4)
1. Найдите точку минимума функции y = x3 – 48x + 17
Ответ: 4
3(x – 4)(x + 4)=0
х = 4, х = - 4
Точка минимума
Найти область определения функции: D(y)=(-∞;+∞)
Слайд 10
Реши самостоятельно!
Ответ: 2
Проверь себя: D(y)=(-∞;+∞)
у
у′
+
-
-
Слайд 11
Реши самостоятельно!
Ответ: -3
Проверь себя: D(y)=(-∞;+∞)
у
у′
+
-
+
Слайд 12
4. Найдите точку минимума функции
y = 2х – ln(x+3) + 7
Ответ: -2,5
Слайд 13
5. Найдите точку минимума функции
Ответ: 2
Слайд 14
6. Найдите точку минимума функции
Ответ: -17
Слайд 15
7. Найдите точку минимума функции
Ответ: 4
0
Слайд 16
8. Найдите точку максимума функции
Ответ: 9
Слайд 17
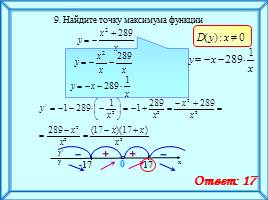
9. Найдите точку максимума функции
Ответ: 17
Слайд 18
10. Найдите точку максимума функции
y = ln(9x+10) – 9х
Ответ: -1
Слайд 19
11. Найдите точку минимума функции
Ответ: -3
Слайд 20
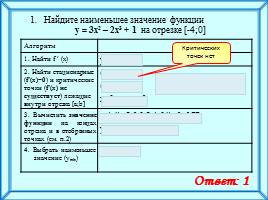
Найдите наименьшее значение функции
y = 3x2 – 2x3 + 1 на отрезке [-4;0]
Алгоритм
1. Найти f ′ (x) у′=6х-6х2
2. Найти стационарные (f′(x)=0) и критические точки (f′(x) не существует) лежащие внутри отрезка [а;b] 6х-6х2=0
6х(1-х)=0
х=0 или х=1
3. Вычислить значение функции на концах отрезка и в отобранных точках (см. п.2) у (-4)=3∙16-2∙(-64)+1=177
у (0) =3∙0-2∙0+1=1
4. Выбрать наименьшее значение (уmin) ymin =1
Ответ: 1
Критических точек нет
Слайд 21
Реши самостоятельно!
Ответ: 0
Проверь себя:
у(1)=-1
у(3)=-3
у(2)=0
Слайд 22
Реши самостоятельно!
Ответ: -32
Проверь себя:
у(-2)=-5
у(2)=-25
у(1)=-32
Слайд 23
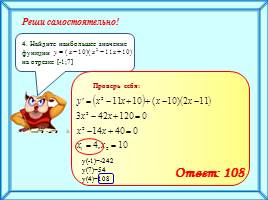
Реши самостоятельно!
Ответ: 108
Проверь себя:
у(-1)=-242
у(7)=54
у(4)=108
Слайд 24
5. Найдите наименьшее значение функции
Ответ: 8
на отрезке [2;8]
Стационарные точки х=-4;4
Критическая точка х=0
Слайд 25
Реши самостоятельно!
Ответ: -7
Проверь себя:
у(-14)=-10,5
у(-1)=-43
у(-7)=-7
х=-7, х=7, х≠0
Слайд 26
Реши самостоятельно!
Ответ: -25
Проверь себя:
у(-10)=-75
у(-1)=-201
у(-5)=-25
Слайд 27
5. Найдите наибольшее значение функции
Ответ: 11
на отрезке [-4;4]
Стационарная точка х=-8,5
Критическая точка х=-5
Слайд 28
Использован материал рабочей тетради С.А. Шестакова «ЕГЭ 2012. Математика. Задача В14. Исследование функции»
 Применение производной к исследованию функций
Применение производной к исследованию функций Применение производной к исследованию функции
Применение производной к исследованию функции Исследование функции с помощью производной
Исследование функции с помощью производной Подготовка урока с элементами исследования
Подготовка урока с элементами исследования Построение и исследование графиков функций с использованием программного обеспечения компьютеров
Построение и исследование графиков функций с использованием программного обеспечения компьютеров Подготовка фонетической стороны речи для сдачи ЕГЭ по английскому языку
Подготовка фонетической стороны речи для сдачи ЕГЭ по английскому языку Основы подготовки к ЕГЭ по английскому языку 2020
Основы подготовки к ЕГЭ по английскому языку 2020