Презентация - Применение производной к исследованию функций

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа с углублённым изучением отдельных предметов с.Тербуны Тербунского района Липецкой области
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
Автор работы: Ешану Валерия Владимировна, 10 А класс   Руководитель: Барабанщикова О.В., учитель математики
Тербуны 2020

Гипотеза: решение задач разных типов на исследование функций с помощью производной развивает математические компетенции и позволяет лучше подготовиться к сдаче экзамена на курс средней школы. Цель: изучение различных способов исследования функций с помощью производной.

Задачи: узнать историю возникновения производной; определить важность производной в исследовании функций; научиться исследовать функции на экстремумы, монотонность, наибольшее и наименьшее значение на отрезке; проанализировать разные типы задач контрольно-измерительных материалов на исследование функций с помощью производной; составить сборник по решению задач на исследование функций для подготовки к ЕГЭ.

Объект исследования: задачи на исследование функций с помощью производной для подготовки к ЕГЭ. Предмет исследования: различные типы задач на исследование функций и способы их решения. Методы исследования: анализ, сравнение и классификация различных типов задач.
Практическая значимость: данная работа поможет моим одноклассникам научиться решать различные типы задач на исследование функций с помощью производной, может быть использована на уроках математики, различных спецкурсах и внеклассных занятиях.

История возникновения:
Исаак Ньютон (1643-1727)
Го́тфрид Ви́льгельм Ле́йбниц (1646-1716)

Использование производной: в физике (ускорение, как производная скорости); химии(определение скорости химической реакции и др.); географии (расчёт некоторых значений сейсмографии и др.); экономике; биологии (расчёт популяции какого-либо вида); алгебре (исследование функций).
Огюсте́н Луи́ Коши́ (1789 – 1857),
впервые сформулировал определение производной

Исследование функций на монотонность
Монотонно возрастающая функция – это функция ,у которой большему значению аргумента соответствует большее значение функции. Монотонно убывающая функция – это функция, у которой большему значению аргумента соответствует меньшее значение функции.
Функция возрастает: f ′(xₒ) ˃ 0 => f (x)↑ Функция убывает: f ′(xₒ) ˂ 0 => f (x)↓

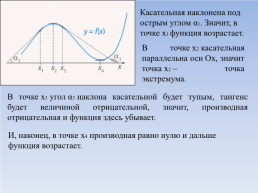
Касательная наклонена под острым углом α1. Значит, в точке x1 функция возрастает.
В точке x2 касательная параллельна оси Ox, значит точка x2 – точка экстремума.
В точке x3 угол α3 наклона касательной будет тупым, тангенс будет величиной отрицательной, значит, производная отрицательная и функция здесь убывает.
И, наконец, в точке x4 производная равно нулю и дальше функция возрастает.

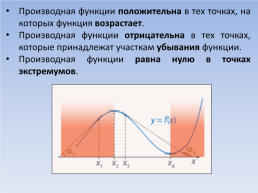
Производная функции положительна в тех точках, на которых функция возрастает. Производная функции отрицательна в тех точках, которые принадлежат участкам убывания функции. Производная функции равна нулю в точках экстремумов.

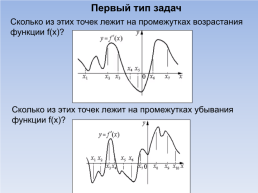
Первый тип задач
Сколько из этих точек лежит на промежутках возрастания функции f(x)?
Сколько из этих точек лежит на промежутках убывания функции f(x)?

Отыскание точек экстремума
Если функция y=f(x) имеет экстремум в точке x=xₒ, то в этой точке производная функции либо равна нулю, либо не существует.
Достаточные условия экстремума: если у точки существует такая окрестность, в которой при x < xₒ выполняется неравенство f'(x) < 0, а при x > xₒ — неравенство f'(x) > 0, то x = xₒ — точка минимума функции y = f(x)); если у точки существует такая окрестность, в которой при x < xₒ выполняется неравенство f'(x)>0, а при x > xₒ — неравенство f'(x) < 0, то x = xₒ — точка максимума функции y = f(x)); если у этой точки существует такая окрестность, что в ней и слева, и справа от точки xₒ знаки производной одинаковы, то в точке xₒ экстремума нет.

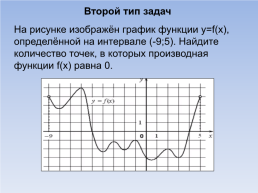
Второй тип задач
На рисунке изображён график функции y=f(x), определённой на интервале (-9;5). Найдите количество точек, в которых производная функции f(x) равна 0.

Физический и геометрический смысл производной
Физический (механический) смысл производной состоит в следующем. Если s(t) — закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени t: v=s′(t). Геометрический смысл производной состоит в следующем. Если к графику функции y=f(x) в точке с абсциссой x=a можно провести касательную, не параллельную оси y, то f′(a) выражает угловой коэффициент касательной: k=f′(a). Поскольку k=tgα, то верно равенство f′(a)=tgα.

Третий тип задач
Материальная точка движется прямолинейно по закону x(t) = 6t2 - 48t + 17 . Найдите её скорость в момент времени t = 9c.
Найдём закон изменения скорости: v(t) = x,(t) = 12t - 48
При t = 9c имеем: v(9) = 12*9 – 48 = 60 м/с
Ответ: 60м/с

Параллельность касательной к графику функции y=f(x) и прямой.
Если касательная параллельна горизонтальной прямой, то она проходит через точки экстремумов. Если касательная параллельна оси абсцисс или совпадает с ней, она имеет вид y = b, и её угловой коэффициент равен 0. Если угловой коэффициент равен нулю, значит и производная равна нулю. Если касательная параллельна какой-либо прямой, то их угловые коэффициенты равны.

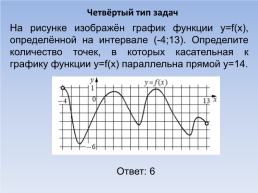
Четвёртый тип задач
На рисунке изображён график функции y=f(x), определённой на интервале (-4;13). Определите количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=14.
Ответ: 6

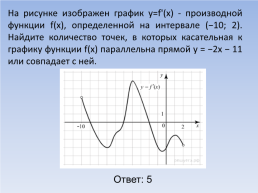
На рисунке изображен график y=f'(x) - производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней.
Ответ: 5

ВЫВОДЫ:
В данной проектной работе была собрана и проанализирована информация по различным типам задач на исследование функций с помощью производной. Изучив теоретический материал по данной теме, я узнала историю возникновения производной, а также убедилась в том, что для успешной сдачи ЕГЭ необходимо уметь решать задачи, используя понятие производной функции. Классифицируя задачи на 4 вида, я научилась исследовать функции на экстремумы, монотонность, использовать физический и геометрический смысл производной, находить наибольшее и наименьшее значение функции на заданном промежутке.

Спасибо за внимание!