Презентация - Исследование функции с помощью производной

Исследование графика функции с помощью производной.
Учитель ЯГЛ Крючкова Е.А. 2014г.

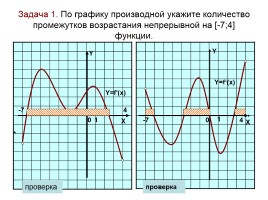
Задача 1. По графику производной укажите количество промежутков возрастания непрерывной на [-7;4] функции.
-7
4
Y=f'(x)
проверка
проверка
0
0
1
1
X
Y
X
Y
Y=f‘(x)
-7
4

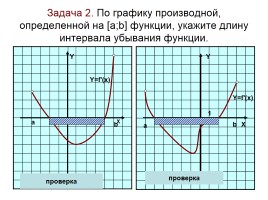
Задача 2. По графику производной, определенной на [а;b] функции, укажите длину интервала убывания функции.
Y
Y
X
X
0
1
0
1
Y=f'(x)
Y=f'(x)
проверка
проверка
а
b
a
b

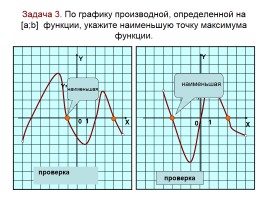
Задача 3. По графику производной, определенной на [а;b] функции, укажите наименьшую точку максимума функции.
Y
Y
0
1
X
0
1
X
Y=f'(x)
Y=f'(x)
проверка
проверка

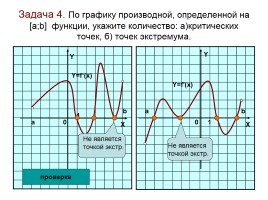
Задача 4. По графику производной, определенной на [а;b] функции, укажите количество: а)критических точек, б) точек экстремума.
Y
Y
0
1
0
1
X
X
Y=f'(x)
Y=f‘(x)
проверка
a
b
a
b

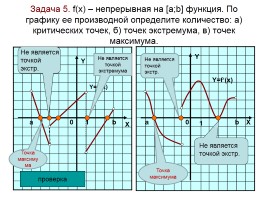
Задача 5. f(x) – непрерывная на [а;b] функция. По графику ее производной определите количество: а) критических точек, б) точек экстремума, в) точек максимума.
0
1
X
Y
а
b
Y
0
1
a
b
X
Y=f‘(x)
Y=f‘(x)
проверка
Не является точкой экстремума
Не является точкой экстр.
Точка максимума
Точка максимума

Решите задачи
1. Найдите значение функции при наименьшем натуральном значении переменной из промежутка (промежутков) убывания функции 2. Найдите суммарную длину промежутков убывания функции У=f(x), если ее производная имеет вид f’(x) =(x²-x-2)(x²-x-12).

Проверим решение задачи
1. Производная имеет вид: f’=[(x+3)(x-5)]/(x-1)² 2. Методом интервалов находим, что производная отрицательна на промежутках (-3;1) и (1;5), значит, на каждом промежутке функция убывает. 3. Наименьшее натуральное значение из полученных промежутков х=2, тогда f(2)=20.

Проверим решение задачи
1. Представим производную в виде f´=(x-2)(x-1)(x+3)(x-4) 2. Решив уравнение f´(x)=0, найдем критические точки: х=-3, х=-1, х=2, х=4. 3. Методом интервалов определим знаки производной на каждом из промежутков. Промежутками убывания являются интервалы [-3;-1] и [2;4]. Суммарная длина промежутков убывания равна 4.

Решите задачи
1. Сколько корней в зависимости от параметра а имеет уравнение
2. При каком значении параметра p уравнение имеет более двух корней.
3. Найдите значения параметра р, при которых уравнение не имеет решений.

Литература
Математика. Сборник заданий «Производная и первообразная» Издательство «экзамен», 2012 Е.А.Семенко, М.В.Фоменко и др