Презентация - Производная функции

Преподаватель ГАПОУ РО «РКТМ» Колыхалина К.А.
Производная функции

Приращение аргумента, приращение функции
Пусть х – произвольная точка, лежащая в некоторой окрестности фиксированной точки х0. Разность х-х0 называется приращением независимой переменной (или приращением аргумента) в точке х0 и обозначается ∆х. ∆х = х – х0 – приращение независимой переменной. Приращением функции f в точке x0 называется разность между значениями функции в произвольной точке и значением функции в фиксированной точке. f(х) – f(х0)=f(х0+∆х) – f(х0) – приращение функции f ∆f=f(х0+∆х) – f(х0)

Определение производной
Производной функции y=f(x) в точке x =x0 называется предел отношения приращения функции ∆y в этой точке к приращению аргумента ∆x, при стремлении приращения аргумента к нулю.

Алгоритм вычисления производной
Производная функции y= f(x) может быть найдена по следующей схеме: 1. Дадим аргументу x приращение ∆x≠0 и найдем наращенное значение функции y+∆y= f(x+∆x). 2. Находим приращение функции ∆y= f(x+∆x) - f(x). 3. Составляем отношение 4. Находим предел этого отношения при ∆x⇾0, т.е. ( если этот предел существует).

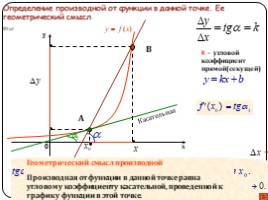
Определение производной от функции в данной точке. Ее геометрический смысл



k – угловой коэффициент прямой(секущей)
А
В
Итог
Геометрический смысл производной Производная от функции в данной точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.

Физический смысл производной 1. Задача об определении скорости движения материальной частицы
Пусть вдоль некоторой прямой движется точка по закону s= s(t), где s- пройденный путь, t- время, и необходимо найти скорость точки в момент t0 . К моменту времени t0 пройденный путь равен s0 = s(t0), а к моменту (t0 +∆t) – путь s0 + ∆s=s(t0 +∆t). Тогда за промежуток ∆t средняя скорость будет Чем меньше ∆t, тем лучше средняя скорость характеризует движение точки в момент t0. Поэтому под скоростью точки в момент t0 следует понимать предел средней скорости за промежуток от t0 до t0 +∆t, когда ∆t⇾0 , т.е.

2. ЗАДАЧА О СКОРОСТИ ХИМИЧЕСКОЙ РЕАКЦИИ
Пусть некоторое вещество вступает в химическую реакцию. Количество этого вещества Q изменяется в течение реакции в зависимости от времени t и является функцией от времени. Пусть за время ∆t количество вещества изменяется на ∆Q , тогда отношение будет выражать среднюю скорость химической реакции за время ∆t, а предел этого отношения - скорость химической реакции в данный момент времени t.

3. ЗАДАЧА ОПРЕДЕЛЕНИЯ СКОРОСТИ РАДИОАКТИВНОГО РАСПАДА
Если m- масса радиоактивного вещества и t- время, то явление радиоактивного распада в момент времени t при условии, что масса радиоактивного вещества с течением времени уменьшается, характеризуется функцией m= m(t). Средняя скорость распада за время ∆t выражается отношением а мгновенная скорость распада в момент времени t .

Физический смысл производной функции в данной точке
.

Производные основных элементарных функций

Основные правила дифференцирования
Пусть u=u(x) и v=v(x) – дифференцируемые функции в точке x. 1) (u  v) = u  v 2) (uv) = uv +uv (cu) = cu 3) , если v  0