Презентация - Применение производной к исследованию функции

Презентация к уроку: “Применение производной к исследованию функции”
Гимназия ДВФУ Класс: 11 Автор: Муравьева Х.И.

№ 1
Прямая y = 7x - 5 параллельна касательной к графику функции y = x² + 6x - 8. Найдите абсциссу точки касания.
№ 2
Прямая y = -4x - 11 является касательной к графику функции y = x³ + 7x² + 7x - 6. Найдите абсциссу точки касания.

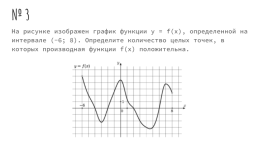
№ 3
На рисунке изображен график функции y = f(x), определенной на интервале (-6; 8). Определите количество целых точек, в которых производная функции f(x) положительна.

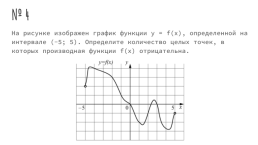
№ 4
На рисунке изображен график функции y = f(x), определенной на интервале (-5; 5). Определите количество целых точек, в которых производная функции f(x) отрицательна.

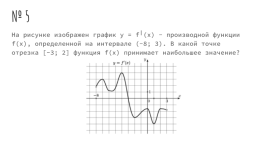
№ 5
На рисунке изображен график y = f╵(x) - производной функции f(x), определенной на интервале (-8; 3). В какой точке отрезка [-3; 2] функция f(x) принимает наибольшее значение?

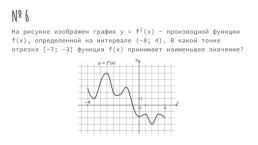
№ 6
На рисунке изображен график y = f╵(x) - производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7; -3] функция f(x) принимает наименьшее значение?

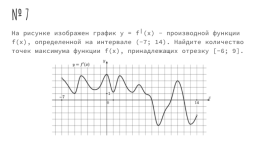
№ 7
На рисунке изображен график y = f╵(x) - производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6; 9].

№ 8
На рисунке изображен график y = f╵(x) - производной функции f(x), определенной на интервале (-18; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13; 1].

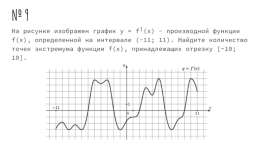
№ 9
На рисунке изображен график y = f╵(x) - производной функции f(x), определенной на интервале (-11; 11). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-10; 10].

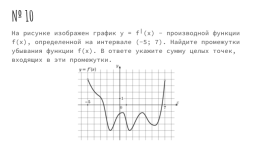
№ 10
На рисунке изображен график y = f╵(x) - производной функции f(x), определенной на интервале (-5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

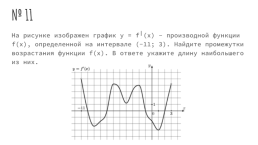
№ 11
На рисунке изображен график y = f╵(x) - производной функции f(x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

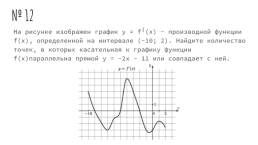
№ 12
На рисунке изображен график y = f╵(x) - производной функции f(x), определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции f(x)параллельна прямой y = -2x - 11 или совпадает с ней.

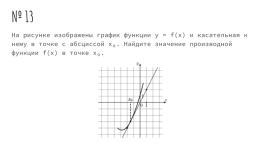
№ 13
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

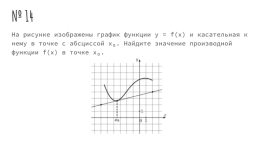
№ 14
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

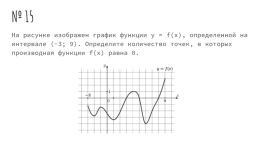
№ 15
На рисунке изображен график функции y = f(x), определенной на интервале (-3; 9). Определите количество точек, в которых производная функции f(x) равна 0.

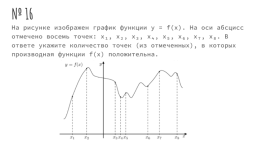
№ 16
На рисунке изображен график функции y = f(x). На оси абсцисс отмечено восемь точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈. В ответе укажите количество точек (из отмеченных), в которых производная функции f(x) положительна.

№ 17
На рисунке изображен график функции y = f(x). На оси абсцисс отмечено двенадцать точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂. В ответе укажите количество точек (из отмеченных), в которых производная функции f(x) отрицательна.

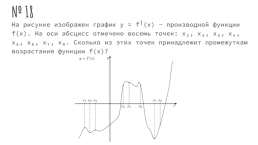
№ 18
На рисунке изображен график y = f╵(x) - производной функции f(x). На оси абсцисс отмечено восемь точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?

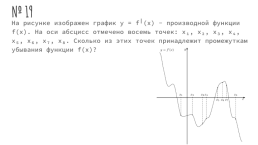
№ 19
На рисунке изображен график y = f╵(x) - производной функции f(x). На оси абсцисс отмечено восемь точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?

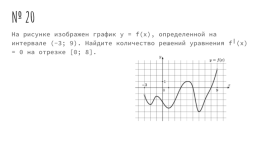
№ 20
На рисунке изображен график y = f(x), определенной на интервале (-3; 9). Найдите количество решений уравнения f╵(x) = 0 на отрезке [0; 8].

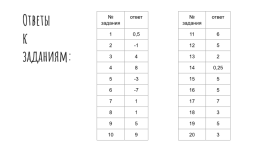
Ответы к заданиям:
№ задания.ответ
1.0,5
2.-1
3.4
4.8
5.-3
6.-7
7.1
8.1
9.5
10.9
№ задания.ответ
11.6
12.5
13.2
14.0,25
15.5
16.5
17.7
18.3
19.5
20.3