Презентация - Двугранный угол
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 95%
- Слайдов: 45
- Просмотров: 999
- Скачиваний: 78
- Размер: 0.44 MB
- Онлайн: Да
- Формат: ppt / pptx
Слайды и текст этой онлайн презентации
Слайд 1

Двугранный угол
Слайд 2
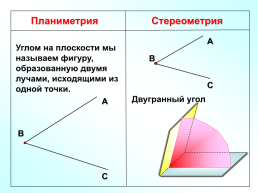
Планиметрия
Стереометрия
Углом на плоскости мы называем фигуру, образованную двумя лучами, исходящими из одной точки.
Двугранный угол
Слайд 3

Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости.
Прямая a – ребро двугранного угла
a
Две полуплоскости – грани двугранного угла
Прямая a – ребро двугранного угла
a
Две полуплоскости – грани двугранного угла
Слайд 4
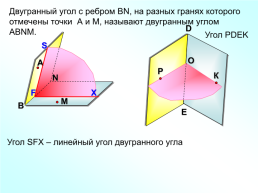
Двугранный угол с ребром ВN, на разных гранях которого отмечены точки А и М, называют двугранным углом АВNМ.
D
Угол РDEK
А
Р
К
N
M
В
E
Угол SFX – линейный угол двугранного угла
D
Угол РDEK
А
Р
К
N
M
В
E
Угол SFX – линейный угол двугранного угла
Слайд 5
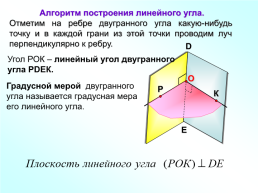
Алгоритм построения линейного угла.
Отметим на ребре двугранного угла какую-нибудь точку и в каждой грани из этой точки проводим луч перпендикулярно к ребру.
D
Угол РОК – линейный угол двугранного угла РDEК.
Градусной мерой двугранного угла называется градусная мера его линейного угла.
E
D
Угол РОК – линейный угол двугранного угла РDEК.
Градусной мерой двугранного угла называется градусная мера его линейного угла.
E
Слайд 6
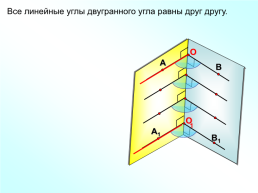
Все линейные углы двугранного угла равны друг другу.
Слайд 7
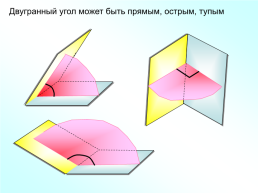
Двугранный угол может быть прямым, острым, тупым
Слайд 8
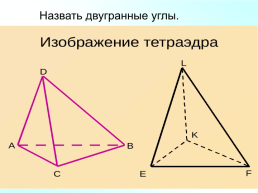
Назвать двугранные углы.
Слайд 9
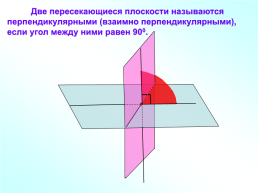
Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900.
Слайд 10
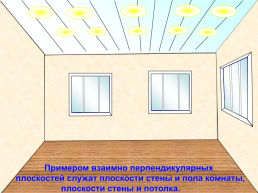
Примером взаимно перпендикулярных плоскостей служат плоскости стены и пола комнаты, плоскости стены и потолка.
Слайд 11
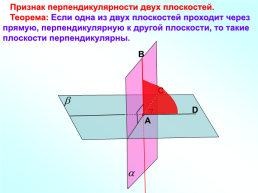
Признак перпендикулярности двух плоскостей.
Теорема: Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
С
А
С
А
Слайд 12
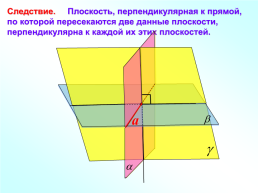
Следствие. Плоскость, перпендикулярная к прямой,
по которой пересекаются две данные плоскости, перпендикулярна к каждой их этих плоскостей.
Слайд 13
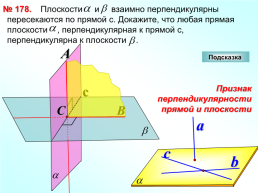
№ 178.
Плоскости и взаимно перпендикулярны пересекаются по прямой с. Докажите, что любая прямая плоскости , перпендикулярная к прямой с, перпендикулярна к плоскости .
Подсказка
c
C
Плоскости и взаимно перпендикулярны пересекаются по прямой с. Докажите, что любая прямая плоскости , перпендикулярная к прямой с, перпендикулярна к плоскости .
Подсказка
c
C
Слайд 14
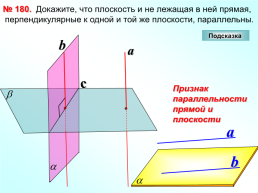
№ 180.
Докажите, что плоскость и не лежащая в ней прямая, перпендикулярные к одной и той же плоскости, параллельны.
Подсказка
c
Докажите, что плоскость и не лежащая в ней прямая, перпендикулярные к одной и той же плоскости, параллельны.
Подсказка
c
Слайд 15
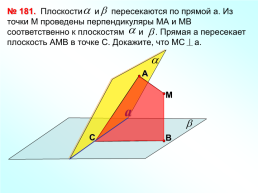
№ 181.
М
a
С
Слайд 16
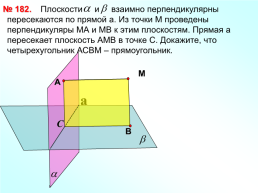
№ 182.
Плоскости и взаимно перпендикулярны пересекаются по прямой a. Из точки М проведены перпендикуляры МА и МВ к этим плоскостям. Прямая а пересекает плоскость АМВ в точке С. Докажите, что четырехугольник АСВМ – прямоугольник.
М
a
С
Плоскости и взаимно перпендикулярны пересекаются по прямой a. Из точки М проведены перпендикуляры МА и МВ к этим плоскостям. Прямая а пересекает плоскость АМВ в точке С. Докажите, что четырехугольник АСВМ – прямоугольник.
М
a
С
Слайд 17
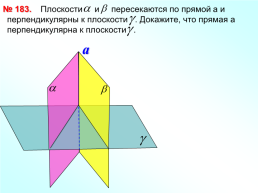
№ 183.
Плоскости и пересекаются по прямой a и перпендикулярны к плоскости . Докажите, что прямая а перпендикулярна к плоскости .
Плоскости и пересекаются по прямой a и перпендикулярны к плоскости . Докажите, что прямая а перпендикулярна к плоскости .
Слайд 18
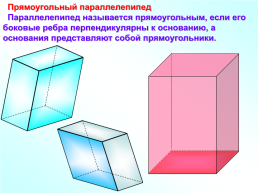
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
Слайд 19

Прямоугольный параллелепипед
Две грани параллелепипеда параллельны.
Две грани параллелепипеда параллельны.
Слайд 20
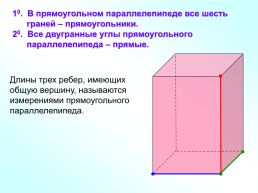
10. В прямоугольном параллелепипеде все шесть
граней – прямоугольники.
20. Все двугранные углы прямоугольного
параллелепипеда – прямые.
Длины трех ребер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.
Длины трех ребер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.
Слайд 21
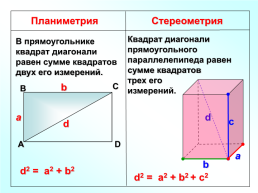
Планиметрия
Стереометрия
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В прямоугольнике квадрат диагонали равен сумме квадратов двух его измерений.
b
С
В
a
d
А
D
d2 = a2 + b2
d2 = a2 + b2 + с2
Слайд 22

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
d2 = a2 + b2 + с2
C1
D1
B1
A1
с
C
D
Следствие. Диагонали прямоугольного параллелепипеда равны.
а
B
b
A
d2 = a2 + b2 + с2
C1
D1
B1
A1
с
C
D
Следствие. Диагонали прямоугольного параллелепипеда равны.
а
B
b
A
Слайд 23
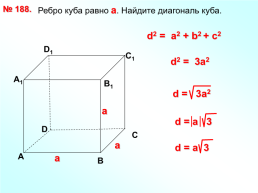
№ 188.
Ребро куба равно а. Найдите диагональ куба.
d2 = a2 + b2 + с2
D1
С1
d2 = 3a2
А1
В1
а
D
С
а
А
а
В
Ребро куба равно а. Найдите диагональ куба.
d2 = a2 + b2 + с2
D1
С1
d2 = 3a2
А1
В1
а
D
С
а
А
а
В
Слайд 24
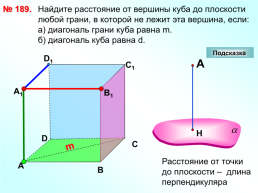
№ 189.
Найдите расстояние от вершины куба до плоскости любой грани, в которой не лежит эта вершина, если: а) диагональ грани куба равна m. б) диагональ куба равна d.
Подсказка
D1
С1
А1
В1
D
С
m
А
В
Найдите расстояние от вершины куба до плоскости любой грани, в которой не лежит эта вершина, если: а) диагональ грани куба равна m. б) диагональ куба равна d.
Подсказка
D1
С1
А1
В1
D
С
m
А
В
Слайд 25
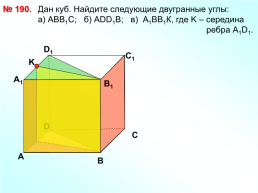
№ 190.
Дан куб. Найдите следующие двугранные углы: a) АВВ1С; б) АDD1B; в) А1ВВ1К, где K – середина ребра А1D1.
D1
С1
А1
В1
D
С
А
В
Дан куб. Найдите следующие двугранные углы: a) АВВ1С; б) АDD1B; в) А1ВВ1К, где K – середина ребра А1D1.
D1
С1
А1
В1
D
С
А
В
Слайд 26
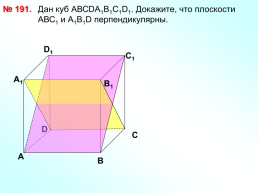
№ 191.
Дан куб АВСDА1В1С1D1. Докажите, что плоскости АВС1 и А1В1D перпендикулярны.
D1
С1
А1
В1
D
С
А
В
Дан куб АВСDА1В1С1D1. Докажите, что плоскости АВС1 и А1В1D перпендикулярны.
D1
С1
А1
В1
D
С
А
В
Слайд 27
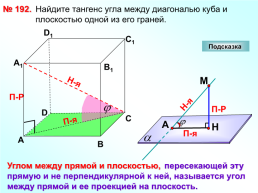
№ 192.
Найдите тангенс угла между диагональю куба и плоскостью одной из его граней.
D1
С1
Подсказка
А1
В1
Н-я
П-Р
D
С
А
В
Найдите тангенс угла между диагональю куба и плоскостью одной из его граней.
D1
С1
Подсказка
А1
В1
Н-я
П-Р
D
С
А
В
Слайд 28
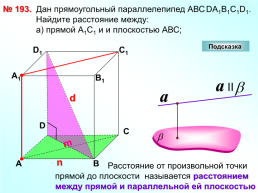
№ 193.
Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите расстояние между: а) прямой А1С1 и и плоскостью АВС;
Подсказка
D1
С1
А1
В1
D
С
А
В
Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите расстояние между: а) прямой А1С1 и и плоскостью АВС;
Подсказка
D1
С1
А1
В1
D
С
А
В
Слайд 29
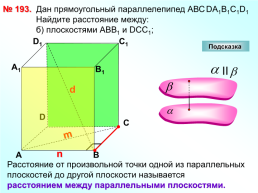
№ 193.
Дан прямоугольный параллелепипед АВСDА1В1С1D1 Найдите расстояние между: б) плоскостями АВВ1 и DCC1;
D1
С1
Подсказка
А1
В1
D
С
А
В
Дан прямоугольный параллелепипед АВСDА1В1С1D1 Найдите расстояние между: б) плоскостями АВВ1 и DCC1;
D1
С1
Подсказка
А1
В1
D
С
А
В
Слайд 30
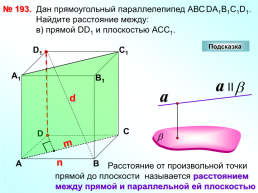
№ 193.
Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите расстояние между: в) прямой DD1 и плоскостью АСС1.
Подсказка
D1
С1
А1
В1
С
D
А
В
Дан прямоугольный параллелепипед АВСDА1В1С1D1. Найдите расстояние между: в) прямой DD1 и плоскостью АСС1.
Подсказка
D1
С1
А1
В1
С
D
А
В
Слайд 31
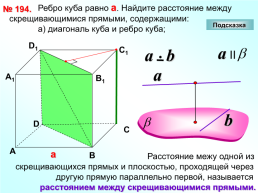
Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащими:
а) диагональ куба и ребро куба;
№ 194.
Подсказка
D1
С1
А1
В1
D
С
А
а
В
№ 194.
Подсказка
D1
С1
А1
В1
D
С
А
а
В
Слайд 32
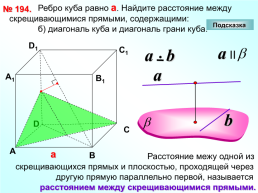
Ребро куба равно а. Найдите расстояние между скрещивающимися прямыми, содержащими:
б) диагональ куба и диагональ грани куба.
№ 194.
Подсказка
D1
С1
А1
В1
D
С
А
а
В
№ 194.
Подсказка
D1
С1
А1
В1
D
С
А
а
В
Слайд 33
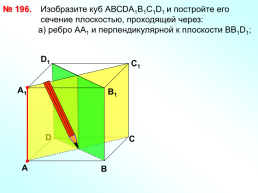
№ 196.
Изобразите куб АВСDА1В1С1D1 и постройте его сечение плоскостью, проходящей через: а) ребро АА1 и перпендикулярной к плоскости ВВ1D1;
D1
С1
А1
В1
D
С
А
В
Изобразите куб АВСDА1В1С1D1 и постройте его сечение плоскостью, проходящей через: а) ребро АА1 и перпендикулярной к плоскости ВВ1D1;
D1
С1
А1
В1
D
С
А
В
Слайд 34
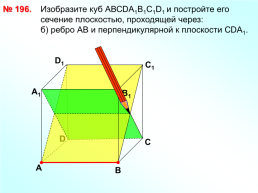
№ 196.
Изобразите куб АВСDА1В1С1D1 и постройте его сечение плоскостью, проходящей через: б) ребро АВ и перпендикулярной к плоскости СDA1.
D1
С1
А1
В1
D
С
А
В
Изобразите куб АВСDА1В1С1D1 и постройте его сечение плоскостью, проходящей через: б) ребро АВ и перпендикулярной к плоскости СDA1.
D1
С1
А1
В1
D
С
А
В
Слайд 35
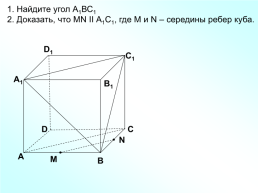
1. Найдите угол А1ВС1
2. Доказать, что MN II А1С1, где M и N – середины ребер куба.
D1
С1
А1
В1
D
С
А
В
D1
С1
А1
В1
D
С
А
В
Слайд 36
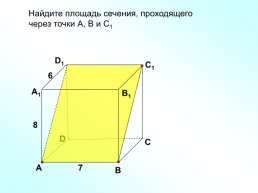
Найдите площадь сечения, проходящего
через точки А, В и С1
D1
С1
А1
В1
D
С
А
В
D1
С1
А1
В1
D
С
А
В
Слайд 37
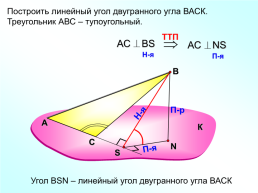
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
В
П-р
Н-я
А
К
С
П-я
Угол ВSN – линейный угол двугранного угла ВАСК
В
П-р
Н-я
А
К
С
П-я
Угол ВSN – линейный угол двугранного угла ВАСК
Слайд 38

Построить линейный угол двугранного угла ВDСК.
АВСD – прямоугольник.
А
В
D
П-р
Н-я
К
П-я
С
Угол ВСN – линейный угол двугранного угла ВDСК
А
В
D
П-р
Н-я
К
П-я
С
Угол ВСN – линейный угол двугранного угла ВDСК
Слайд 39
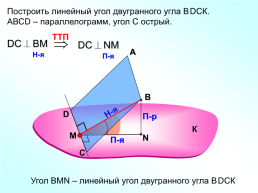
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С острый.
А
В
Н-я
D
П-р
К
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
А
В
Н-я
D
П-р
К
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
Слайд 40
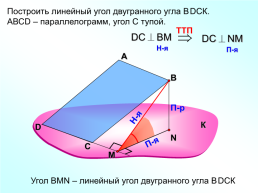
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С тупой.
А
В
П-р
Н-я
К
D
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
А
В
П-р
Н-я
К
D
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
Слайд 41
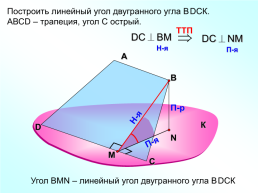
Построить линейный угол двугранного угла ВDСК.
АВСD – трапеция, угол С острый.
А
В
П-р
Н-я
К
D
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
А
В
П-р
Н-я
К
D
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
Слайд 42
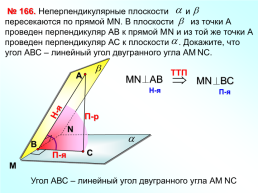
№ 166.
А
Н-я
П-р
N
П-я
M
Угол АВС – линейный угол двугранного угла АМNC
Слайд 43
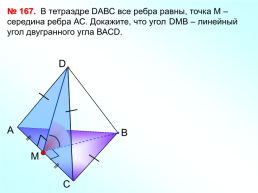
В тетраэдре DАВС все ребра равны, точка М – середина ребра АС. Докажите, что угол DМВ – линейный угол двугранного угла ВАСD.
№ 167.
D
А
В
M
С
№ 167.
D
А
В
M
С
Слайд 44
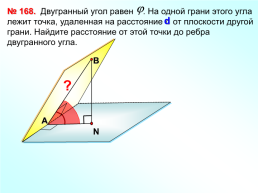
Двугранный угол равен . На одной грани этого угла лежит точка, удаленная на расстояние d от плоскости другой грани. Найдите расстояние от этой точки до ребра двугранного угла.
№ 168.
d
В
?
А
№ 168.
d
В
?
А
Слайд 45
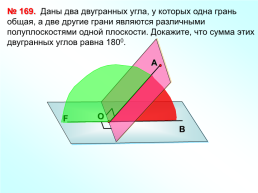
Даны два двугранных угла, у которых одна грань общая, а две другие грани являются различными полуплоскостями одной плоскости. Докажите, что сумма этих двугранных углов равна 1800.
№ 169.
А
№ 169.
А
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.







