Слайды и текст этой онлайн презентации
Слайд 1
Л.С. Атанасян "Геометрия 10-11"
Двугранный угол
Слайд 2
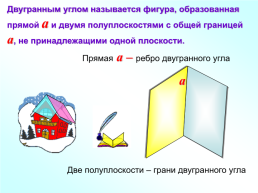
Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости.
Прямая a – ребро двугранного угла
a
Две полуплоскости – грани двугранного угла
Слайд 3
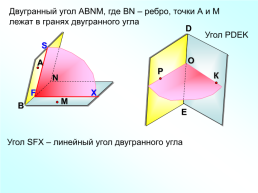
Двугранный угол АВNМ, где ВN – ребро, точки А и М лежат в гранях двугранного угла
D
Угол РDEK
А
Р
К
N
M
В
E
Угол SFX – линейный угол двугранного угла
Слайд 4
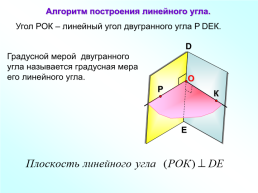
Алгоритм построения линейного угла.
Угол РОК – линейный угол двугранного угла РDEК.
D
Градусной мерой двугранного угла называется градусная мера его линейного угла.
E
Слайд 5
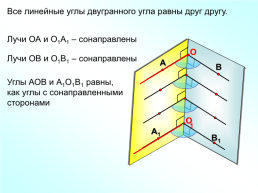
Все линейные углы двугранного угла равны друг другу.
Лучи ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и А1О1В1 равны,
как углы с сонаправленными сторонами
Слайд 6
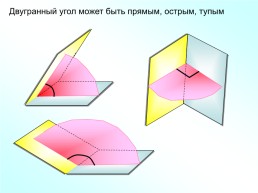
Двугранный угол может быть прямым, острым, тупым
Слайд 7
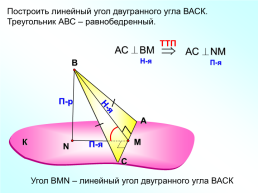
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
В
П-р
Н-я
А
К
П-я
С
Угол ВMN – линейный угол двугранного угла ВАСК
Слайд 8
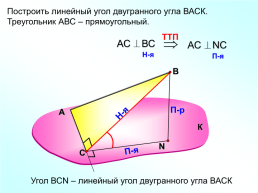
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
В
П-р
А
Н-я
К
П-я
С
Угол ВСN – линейный угол двугранного угла ВАСК
Слайд 9
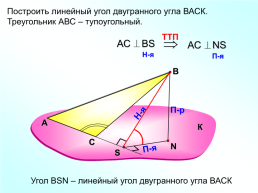
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
В
П-р
Н-я
А
К
С
П-я
Угол ВSN – линейный угол двугранного угла ВАСК
Слайд 10
Задача :
Из вершины В треугольника АВС, сторона АС которого лежит в плоскости α, проведен к этой плоскости перпендикуляр ВВ1. Найдите расстояние от точки В до прямой АС и до плоскости α, если АВ=2, ∠ВАС=1500 и двугранный угол ВАСВ1 равен 450.
Слайд 11
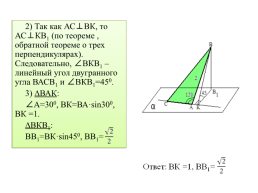
2) Так как АС⊥ВК, то АС⊥КВ1 (по теореме , обратной теореме о трех перпендикулярах). Следовательно, ∠ВКВ1 – линейный угол двугранного угла ВАСВ1 и ∠ВКВ1=450.
3) ∆ВАК:
∠А=300, ВК=ВА·sin300, ВК =1.
∆ВКВ1:
ВВ1=ВК·sin450, ВВ1=
Слайд 12
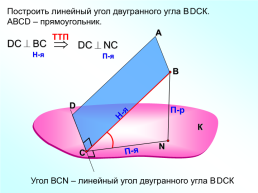
Построить линейный угол двугранного угла ВDСК.
АВСD – прямоугольник.
А
В
D
П-р
Н-я
К
П-я
С
Угол ВСN – линейный угол двугранного угла ВDСК
Слайд 13
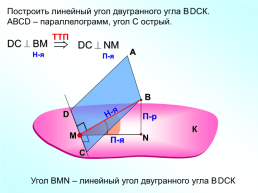
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С острый.
А
В
Н-я
D
П-р
К
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
Слайд 14
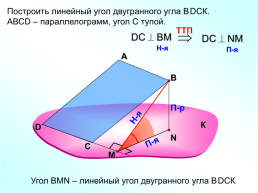
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С тупой.
А
В
П-р
Н-я
К
D
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
Слайд 15
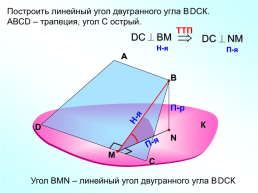
Построить линейный угол двугранного угла ВDСК.
АВСD – трапеция, угол С острый.
А
В
П-р
Н-я
К
D
П-я
С
Угол ВMN – линейный угол двугранного угла ВDСК
Слайд 16
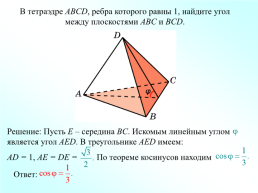
В тетраэдре ABCD, ребра которого равны 1, найдите угол между плоскостями ABC и BCD.
Слайд 17
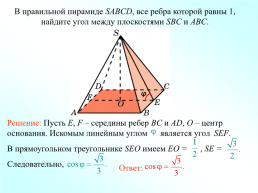
В правильной пирамиде SABCD, все ребра которой равны 1, найдите угол между плоскостями SBC и ABC.
Слайд 18
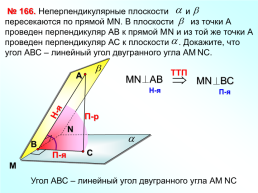
№ 166.
А
Н-я
П-р
N
П-я
M
Угол АВС – линейный угол двугранного угла АМNC
Слайд 19
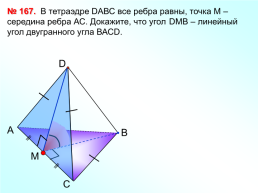
В тетраэдре DАВС все ребра равны, точка М – середина ребра АС. Докажите, что угол DМВ – линейный угол двугранного угла ВАСD.
№ 167.
D
А
В
M
С
Слайд 20
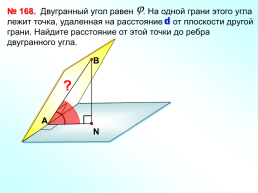
Двугранный угол равен . На одной грани этого угла лежит точка, удаленная на расстояние d от плоскости другой грани. Найдите расстояние от этой точки до ребра двугранного угла.
№ 168.
d
В
?
А
Слайд 21
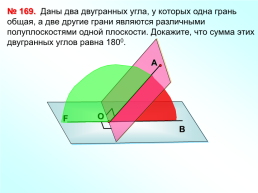
Даны два двугранных угла, у которых одна грань общая, а две другие грани являются различными полуплоскостями одной плоскости. Докажите, что сумма этих двугранных углов равна 1800.
№ 169.
А
 Решение задач по теме: «аксиомы стереометрии. Взаимное расположение прямых в пространстве. Угол между двумя прямыми". Геометрия 10 класс
Решение задач по теме: «аксиомы стереометрии. Взаимное расположение прямых в пространстве. Угол между двумя прямыми". Геометрия 10 класс Геометрия 8 класс «Многоугольники»
Геометрия 8 класс «Многоугольники» Треугольники. Тренировочные задания геометрия 7 класс
Треугольники. Тренировочные задания геометрия 7 класс Урок геометрии в 8 классе. Определение подобных треугольников
Урок геометрии в 8 классе. Определение подобных треугольников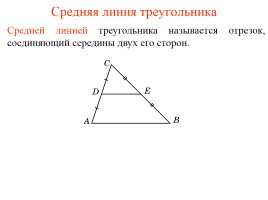 Задачи по геометрии «Средняя линия треугольника»
Задачи по геометрии «Средняя линия треугольника» Урок геометрии в 7 классе «Треугольники»
Урок геометрии в 7 классе «Треугольники» Урок геометрии Равнобедренные треугольники
Урок геометрии Равнобедренные треугольники