Презентация - Геометрия

Продолжите фразу:
Если две плоскости имеют общую точку, то ....
… они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Продолжите фразу:
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает её, то …
… линия пересечения плоскостей параллельна данной прямой.
a

Продолжите фразу:
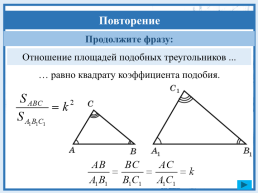
Отношение площадей подобных треугольников ...
… равно квадрату коэффициента подобия.

Свойства средней линии треугольника
Средняя линия параллельна одной из сторон треугольника и равна её половине:
1.
Три средние линии треугольника делят его на 4 равных треугольника, подобных данному.
2.
K

Определение
Две плоскости называются параллельными, если они не пересекаются
α
β

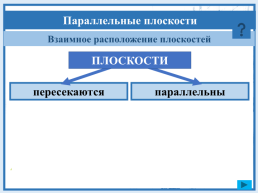
Взаимное расположение плоскостей
ПЛОСКОСТИ
пересекаются
параллельны
β
α

Признак параллельности двух плоскостей
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
a
b
M
α
a₁
b₁
Доказательство:
M₁
β

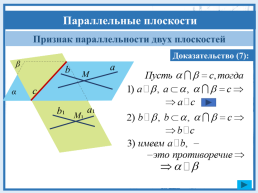
Признак параллельности двух плоскостей
Доказательство (7):
β
a
b
M
с
α
a₁
b₁
M₁

Ещё один признак параллельности двух плоскостей
Если две пересекающиеся прямые одной плоскости параллельны другой плоскости, то эти плоскости параллельны.
Доказательство (4):
K
n
m
c
α
β

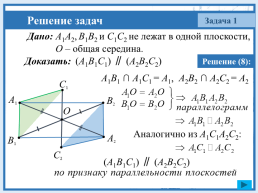
Задача 1
Дано: A1A2, B1B2 и C1C2 не лежат в одной плоскости,
O – общая середина.
Доказать:
(A1B1C1) ∥ (A2B2C2)
Решение (8):
A1B1 ∩ A1C1 = A1, A2B2 ∩ A2C2 = A2
C1
A1
B2
O
Аналогично из A1C1A2C2:
A2
B1
C2
(A1B1C1) ∥ (A2B2C2)

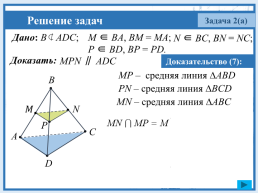
Задача 2(а)
Дано: B ⊄ ADC;
M ∈ BA, BM = MA;
N ∈ BC, BN = NC;
P ∈ BD, BP = PD.
Доказать:
МРN ∥ ADC
Доказательство (7):
MP – средняя линия ∆ABD
B
PN – средняя линия ∆BCD
MN – средняя линия ∆ABC
M
N
P
C
A
D

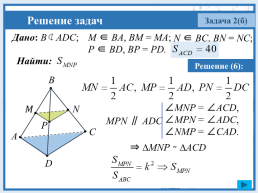
Задача 2(б)
Дано: B ⊄ ADC;
M ∈ BA, BM = MA;
N ∈ BC, BN = NC;
P ∈ BD, BP = PD.
Найти:
Решение (6):
B
∠MNP = ∠ACD, ∠MPN = ∠ADC, ∠NMP = ∠CAD.
M
N
МРN ∥ ADC
P
C
A
⇒ ∆MNP ∼ ∆ACD
D

Фон презентации
Комната без мебели
Презентации к урокам