Презентация - Геометрия Лобачевского

Геометрия Лобачевского
Подготовила: ученица 9 класса Отрадненской средней школы Г.Ульяновска Мушарапова Гулюза. Руководитель: учитель математики Ляхова Л.А.

Предисловие
Геометрия Лобачевского основана на евклидовой геометрии, кроме аксиомы параллельности. Его аксиома является точным отрицанием аксиомы Евклида. Долгое время люди думали, можно ли таким образом обращаться с аксиомами, были многочисленные попытки доказать противоречивость изменённой системы аксиом. Но, когда Лобачевский создал элементарные модели геометрии, стало понятно, что она не более противоречива, чем Евклидова геометрия.

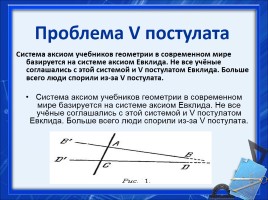
Проблема V постулата
Система аксиом учебников геометрии в современном мире базируется на системе аксиом Евклида. Не все учёные соглашались с этой системой и V постулатом Евклида. Больше всего люди спорили из-за V постулата. Система аксиом учебников геометрии в современном мире базируется на системе аксиом Евклида. Не все учёные соглашались с этой системой и V постулатом Евклида. Больше всего люди спорили из-за V постулата.

Николай Иванович Лобачевский (1792-1856гг.)
Все! Перечеркнуты «Начала». Довольно мысль на них скучала, Хоть прав почти во всем Евклид, Но быть не вечно постоянству: И плоскость свернута в пространство, И мир Иной имеет вид… Н. И. Лобаче́вский  — русский математик, один из создателей неевклидовой геометрии, деятель университетского образования и народного просвещения. Выдающийся математик заменил V постулат евклидовой геометрии и пришёл к выводу, что можно построить другую геометрию, отличную от евклидовой.

Попытки доказательства пятого постулата
Отправным пунктом геометрии Лобачевского является V постулат Евклида — аксиома, равносильная аксиоме о параллельных.. Он входил в список постулатов в «Началах» Евклида. Сложность его формулировки и вызывала попытки вывести его как теорему из остальных постулатов Евклида. Доказать этот постулат пытались многие учёные: Птолемей, Омар Хайям, Катальди и др.

В геометрии Лобачевского:Через каждую точку вне прямой проходят по крайней мере две прямые, лежащие с исходной прямой в одной плоскости, но не пересекающие ее. В 1832 году к аналогичным выводам пришел Бойай. Также, судя по всему, Гаусс знал о существовании неевклидовой геометрии, но не публиковал работ на эту тему. Геометрия Лобачевского, с современной точки зрения, представляет собой геометрию пространства постоянной отрицательной кривизны. Представление о ней можно получить, изучая модели плоскости Лобачевского, такие как модель Клейна, модели Пуанкаре и др. Геометрия Лобачевского нашла свои приложения в современной физике, прежде всего в теории относительности, квантовой физике, теории суперструн.

Применение
Геометрия Лобачевского применяется в разных областях деятельности человека и науках: в географии, в астрономии, в релятивистской физике, в физике высоких энергий, в теории относительности, а также в теории чисел, в её геометрических методах, объединённых под названием «геометрия чисел» .

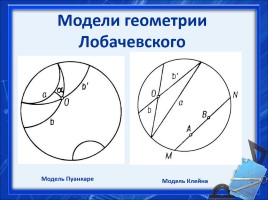
Модели геометрии Лобачевского
Модель Пуанкаре
Модель Клейна

Модель гиперболического параболоида в двухмерном пространстве
Геометрия Лобачевского совершенно верна, если ее рассматривать не на плоскости, а на поверхности гиперболического параболоида (вогнутой поверхности, напоминающей седло)

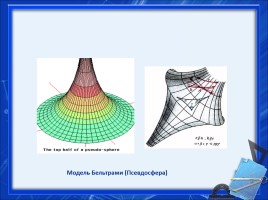
Модель Бельтрами (Псевдосфера)

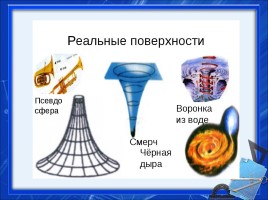
Поверхность Лобачевского с отрицательной кривизной
Бутылка Клейна. В отличие от обыкновенной бутылки у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара можно пройти путь изнутри наружу, не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).

Значение геометрии Лобачевского
Создание геометрии Лобачевского оказало огромное влияние на все естественные науки. Её результаты используются внутри математики – в теории чисел, в теории функций комплексного переменного, в математическом анализе, в частности сам Лобачевский с помощью своей геометрии вычислил около 200 интегралов. Но наиболее широкое применение она нашла в современной физике – общей и специальной теории относительности, в квантовой механике и других областях. Значение геометрии Лобачевского для науки состоит в том, что она разрушила приобретенные веками взгляды на окружающий мир, вывела ученых из узких рамок созданных ими стереотипов мышления. Они стали более восприимчивы к новым неожиданным научным открытиям. Это касается не только математики.

Ученые пришли к выводу, что существование в микромире волн-частиц – такое образование, с которым мы не встречаемся в повседневной жизни. А в дальнейшем были высказаны принципы других ученых, предположения относительно микро- и макромира, которые, казалось, вообще противоречат здравому смыслу. Мы привыкли представлять себе весь мир и все его явления по аналогии с окружающей нас действительностью. Эти представления мы переносим и на макро- и микромир, а они могут быть устроены иначе, и процессы, происходящие там, настолько могут отличатся от известных нам, что «здравый» смысл здесь не всегда помогает. Осознать это позволило создание новой геометрии. Принципы построения неевклидовой геометрии Лобачевского, когда одна аксиома заменяется на противоположную, а остальные остаются без изменений, лёг в основу создания других геометрий.

Заключение
Геометрия Лобачевского долгое время была забыта, но сейчас она нашла широкое применение в физике и астрономии. Я уверена, что и дальше интерес к ней будет возрастать, ведь работы Лобачевского актуальны и в наше время, в период, когда наука и прогресс не стоят на месте, а движутся вперед, к новым истинам. Познакомившись с работами по геометрии Лобачевского, можно согласиться со словами Николая Ивановича : «…в нашем уме не может быть никакого противоречия, когда мы допускаем, что некоторые силы в природе следуют одной, другие своей особой геометрии…». Геометрия Лобачевского заставляет меня взглянуть на мир иначе, задуматься над кажущейся простотой того, что окружает нас. Может быть, все понятия, истины, законы, которые открывали ученые веками и к которым мы так привыкли, не имеют смысла, стоит их только перенести в другую среду. Кто сказал, что законы, действительные на земле, имеют смысл в других галактиках?