Презентация - Геометрия Лобачевского

Геометрия Лобачевского
Выполнила студентка 20-ПСА-3.9 Старцева Кристина

Николай Иванович Лобачевский
Николай Иванович Лобачевский- русский математик, создатель неевклидовой геометрии, деятель университетского образования и народного просвещения. Лобачевский высказал идею, построил и развил новую геометрию, логически столь же совершенную и богатую выводами, как евклидова, несмотря на её несоответствие обычным наглядным представлениям. Лобачевский рассматривал свою геометрию как возможную теорию пространственных отношений.

ПОСТУЛАТЫ ЕВКЛИДА -ПОСТУЛАТЫ ЛОБАЧЕВСКОГО
1. Через две точки можно провести одну и только одну прямую 2. Прямая продолжается бесконечно 3. Из любого центра можно провести окружность любым радиусом 4. Все прямые углы равны между собой

Открытие Лобачевского, не получившее признание современников, совершило переворот в представление о природе пространства, в основе которой более 2 тысяч лет лежало учение Евклида, и оказало огромное влияние на развитие математического мышления. Деятельность Лобачевского вызывает изумление. Ему было всего 34 года, когда он решил «многовековую» проблему V постулата из «Начал» Евклида и построил свою, неевклидову геометрию. Анализируя попытки доказать V постулат, Лобачевский сделал чрезвычайно смелый вывод о его недоказуемости. Раз V постулат недоказуем как теорема, то принципиально возможна другая геометрия, отличная от евклидовой, - неевклидова геометрия, отправной точкой которой является отрицание V постулата.

Пятый постулат Евклида
Если две прямые пересекаются третьей так, что по какую-либо сторону от нее сумма внутренних углов меньше двух прямых углов, то по эту же сторону исходные прямые пересекаются.
Стремление доказать пятый постулат сравнивают с исступленным желанием найти «философский камень» в средние века или с бесчисленными попытками создать «вечный двигатель».

Некоторые эквиваленты пятого постулата
Существует четырёхугольник, у которого все углы прямые. Через каждую точку внутри острого угла всегда можно провести прямую, пересекающую обе его стороны . Если две прямые в одну сторону расходятся, то в другую – сближаются. Сближающиеся прямые рано или поздно пересекутся. Точки, равноудалённые от данной прямой (по одну её сторону), образуют прямую, Существует треугольник, сумма углов которого равна двум прямым. Прямая, пересекающая одну из параллельных прямых, непременно пересечёт и другую. Через любые три точки можно провести либо прямую, либо окружность. Отношение длины окружности к её диаметру является константой, то есть одинаково для любой окружности.

АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ (V ПОСТУЛАТ)
На плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную.
На плоскости через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
а
М
в

Труды Н. И. Лобачевского
1829 – 1830 - «О началах геометрии» 1835 - "Воображаемая геометрия" 1836 - "Применение воображаемой геометрии к некоторым интегралам"
1835-1838 - "Новые начала геометрии с полной теорией параллельных" 1840 - "Геометрические исследования по теории параллельных" 1855 - «Пангеометрия»

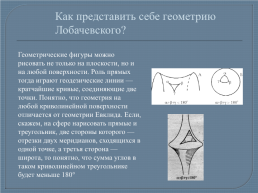
Как представить себе геометрию Лобачевского?
Геометрические фигуры можно рисовать не только на плоскости, но и на любой поверхности. Роль прямых тогда играют геодезические линии — кратчайшие кривые, соединяющие две точки. Понятно, что геомет­рия на любой криволинейной поверхности отличается от геометрии Ев­клида. Если, скажем, на сфере нарисовать прямые и треугольник, две стороны которого — от­резки двух меридианов, сходящихся в одной точке, а третья сторона — широта, то по­нятно, что сумма углов в таком криволиней­ном треугольнике будет меньше 180°

Поверхности локально постоянной отрицательной кривизны
Многие поверхности локально постоянной отрицательной кривизны названы именами математиков, которые их исследовали и описали:
Поверхность Дини (слева) и поверхность Бианки - Амслера (справа)
Псевдосферические поверхности вращения

Если геометрия Евклида является только частью геометрии Лобачевского, то выходит, что наш мир – не мир Евклида. Почему же мы не замечаем разницы. Рассмотрим такое понятие как гауссова кривизна пространства. Если мы возьмем кривую поверхность, проведем к какой-то точке касательную, проведем в точку касания отрезок, перпендикулярный касательной плоскости, то мы получим нормаль. Проведя через нормаль плоскость, мы можем найти окружность, наиболее плотно прилегающую к поверхности. Так как мы можем провести сколько угодно плоскостей, то мы можем найти окружности с минимальным и максимальным радиусами. Используя определенные соотношения, можно определить кривизну пространства, которая может быть как положительная, так и отрицательная.

Геометрия Лобачевского в реальном мире
На поверхностях с отрицательной кривизной и работает геометрия Лобачевского. Именно такую кривизну имеют графики интенсивности всех электромагнитных полей. Состояние поверхности плазмы также описывается геометрией Лобачевского. Сам Лобачевский применил свою геометрию к вычислению определённых интегралов. Геометрия Лобачевского находит применение также в теории чисел, в её геометрических методах, объединённых под названием «геометрия чисел». Была установлена тесная связь геометрии Лобачевского с кинематикой специальной (частной) теории относительности.

Поверхности Лобачевского вокруг нас
У обычного тора поверхность имеет как седлообразные участки с отрицательной кривизной, так и сфероподобные участки с положительной кривизной. Можно сказать, что в некоторой степени тор снаружи - это подобие пространства Римана, а внутри - пространства Лобачевского.

Геометрия Лобачевского в реальном мире
В XX веке было обнаружено, что геометрия Лобачевского имеет важное значение не только для абстрактной математики. Оказалось, что пространство скоростей специальной теории относительности является пространством Лобачевского. Геометрия Лобачевского с успехом используется при изучении столкновений элементарных частиц и при ядерных исследованиях. Например, в расчетах современных синхрофазотронов используются формулы геометрии Лобачевского.

Заключение
Создание геометрии Лобачевского оказало огромное влияние на все науки. Ее результаты используются внутри математики и физики. Непреходящее значение открытия геометрии Лобачевского для науки состоит в том, что оно разрушило приобретенные веками традиционные взгляды на окружающий мир, вывело ученых из узких рамок созданных ими стереотипов мышления. Они стали более восприимчивы к новым неожиданным научным открытиям.

Спасибо за внимание!