Презентация - Sbornik_Krylova_2023 все виды задач

Тема 15 КЕГЭ
Сборник Крылова С.С. 2023

2
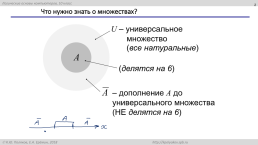
Что нужно знать о множествах?
U – универсальное множество
(все натуральные)
A
– дополнение A до универсального множества (НЕ делятся на 6)

3
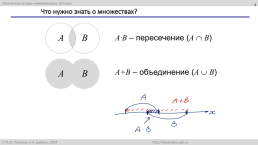
Что нужно знать о множествах?
A·B – пересечение (A  B)
A+B – объединение (A  B)

Типы задач по теме 15 КЕГЭ
Делители Отрезки Треугольники Координатная плоскость Поразрядная конъюнкция (нет в сборнике Крылова С.С. 2023, но была на пробном экзамене 17 мая 2023г. ) Программы для повторения Множества???

Делители

Левая часть логического выражения обязательно в скобках
for a in range(100, 1, -1): for x in range(1, 100): if ((x % a != 0) <= ((x % 6 == 0) <= (x % 4 != 0))) == False: break else: print(a) break
Наибольшее значение A равно 12. Ответ: 12

Демоверсия КЕГЭ 2023 №15 https://www.youtube.com/watch?v=o9cy7V7g3OU&t=678s

Демоверсия КЕГЭ 2023 №15 https://www.youtube.com/watch?v=QVRIC7jlBmI&t=874s
for a in range(1,1000): for x in range(1, 1000): if (((x % 2 == 0) <= (x % 3 != 0)) or (x +a >= 100)) == False: break else: print(a) break
Ответ: 94

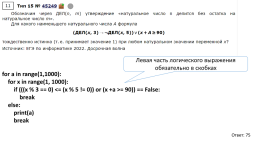
Левая часть логического выражения обязательно в скобках
for a in range(1,1000): for x in range(1, 1000): if (((x % 3 == 0) <= (x % 5 != 0)) or (x +a >= 90)) == False: break else: print(a) break
Ответ: 75

Без проверки условия во втором цикле + импликацию заменили на дизъюнкцию
for A in range(1, 10000): T=True for x in range(1, 10000): T=T*(((x%3)!=0) or ((x%5)!=0) or (x+A>=90)) if T: print(A) break
Импликацию не заменяли на дизъюнкцию for A in range(1, 10000): T=True for x in range(1, 10000): T=T*(((x%3)==0) <= ((x%5)!=0) or (x+A>=90)) if T: print(A) break

Следовательно, необходимо подобрать такое число, которое будет являться наибольшим общим делителем для х = 120 и х = 180. Наибольшим таким А является число 60.

for a in range(100, 1, -1): for x in range(1, 100): if ((120 % a == 0) and ((x % 36 == 0) <= ((x % a != 0) <= (x % 45 != 0))))== False: break else: print(a) break

Рассмотрим такие x, при которых выражение
будет ложным.
Это x, на которые одновременно делятся без остатка 780 и 180. Наибольший общий делитель этих чисел равен 60.
Чтобы найти наименьшее А, необходимо подобрать такое число, которое будет являться наименьшим общим кратным для чисел 60 и 40. Наименьшим таким А является число 120.

Вариант 1 Сборник ФИПИ Крылов 2023
Ответ: 227

Вариант 2 Сборник ФИПИ Крылов 2023
Ответ: 80

Вариант 9 Сборник ФИПИ Крылов 2023
Ответ: 162

Вариант 10 Сборник ФИПИ Крылов 2023
Ответ: 338

Вариант 11 Сборник ФИПИ Крылов 2023
Ответ: 24

Вариант 12 Сборник ФИПИ Крылов 2023
Ответ: 54

Отрезки

p=list(range(5,14)) q=list(range(8,21)) a = [] for x in range(1,50): if not(((x in q)<=(x in p))or(x in a)): a.append(x) print(a)
[14, 15, 16, 17, 18, 19, 20]

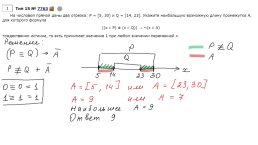
Примечание 1. Следует различать задания «найдите длину отрезка» и «найдите количество целых чисел на отрезке». Длина отрезка равна расстоянию между его граничными точками. Длину отрезка можно вычислить по формуле m−n, где m и n — правая и левая границы этого отрезка соответственно. Длина отрезка не зависит от того, включены ли в него его границы. Заметим, однако, что если границы не включены, то должно использоваться слово «интервал», а не слово «отрезок». Количество целых чисел на отрезке можно найти по формуле m − n + 1, где m и n — правая и левая границы этого отрезка соответственно, причем они входят в отрезок. Примечание 2. Предостерегаем читателей от решения этой и подобных задач с помощью программ, реализующих метод перебора. В программах, которые предлагают наши читатели, в качестве границ отрезка используются целые числа, и длина отрезка определяется как разность между ними. Такие программы будут давать неверный результат, если интервал А не является отрезком, то есть одна или обе из его границ ему не принадлежат. Примером такой задачи является задача 34541.

Примечание 2. Для задачи 15. Предостерегаем читателей от решения этой и подобных задач с помощью программ, реализующих метод перебора. В программах, которые предлагают наши читатели, в качестве границ отрезка используются целые числа, и длина отрезка определяется как разность между ними. Такие программы будут давать неверный результат, если интервал А не является отрезком, то есть одна или обе из его границ ему не принадлежат. В частности, в данной задаче число 38 не должно принадлежать интервалу А, следовательно, программой будет найдена левая граница, равная 39, и правая граница, равная 57, в результате чего длина интервала А получится равной 18. Однако в задаче рассматриваются не целые, а вещественные числа, поэтому длина интервала (38; 57] равна 19.

b=list(range(10,16)) c=list(range(20,28)) a = [] for x in range(1,100): if (not(((x in b)or(x in c))<=(x in a))): a.append(x) print(a)

№15 Вариант 5 Сборник ФИПИ 2023

Вариант 6 Сборник ФИПИ Крылов 2023
Ответ:26

Вариант 7 Сборник ФИПИ Крылов 2023
Ответ: 13

Вариант 8 Сборник ФИПИ Крылов 2023
Ответ: 36

Треугольники

№15 Вариант 3 Сборник ФИПИ 2023
def Treug(n, m, k): return n + m > k and n + k > m and k + m > n for a in range(1000,1,-1): for x in range(1, 1000): if (not((Treug(x,11,18)==(max(x,5)<=15)) and (Treug(x,a,5))))== False: break else: print(a) break
Если логическое выражение для всех x истинно, то выполняется команда по else
Ответ: 24

№15 Вариант 4 Сборник ФИПИ 2023
def Treug(n, m, k): return n + m > k and n + k > m and k + m > n for a in range(1000,1,-1): for x in range(1, 1000): if (not((Treug(x,12,20)==(max(x,5)<=28)) and Treug(x,a,3)))== False: break else: print(a) break
Ответ 6

Координатная плоскость

Вариант 13 Сборник ФИПИ Крылов 2023
Ответ: 15

Вариант 13 Сборник ФИПИ Крылов 2023
for A in range(300,-1,-1): k = 0 for x in range(300): for y in range(300): if ((x >= A) or (y >= A) or (x * y <= 200)): k += 1 if k == 90_000: print(A) break
Ответ: 15

Вариант 14. Сборник ФИПИ Крылов 2023
Ответ: 17

Вариант 20 Сборник Крылова 2023
Ответ: 11

Вариант 20 Сборник Крылова 2023
for A in range(300): k = 0 for x in range(300): for y in range(300): if (y + 2*x <=27) <= ((y - x > 3) or (y <= A)): k += 1 if k == 90_000: print(A) break
Ответ: 11

Вариант 20 Сборник Крылова 2023
Ответ: 11

Функция all () в Python принимает в качестве параметра любой итерабельный объект: список, кортеж, множество словарь или диапазон. Данная функция возвращает True, если все элементы итерируемого объекта равняются True, а в противном случае — False. Любой числовой тип данных, кроме нуля, равняется True, а любая строка, содержащая более одного символа, также равняется True.
Функция any интересуется значениями True и возвращает True, находя первое из них, или False — если не нашла ни одного. А функция all действует с точностью до наоборот. Она ищет значения False и возвращает False, когда найдёт первое такое значение, или возвращает True, если ни одного значения False не нашла.

Вариант 15 Сборник Крылова 2023
Ответ: 25

Вариант 16 Сборник Крылова 2023
Ответ: 35

Вариант 17 Сборник Крылова 2023
Ответ: 61

Вариант 18 Сборник Крылова 2023
Ответ: 61

Вариант 19 Сборник Крылова 2023
Ответ: 9

Поразрядная конъюнкция (нет в сборнике Крылова С.С. 2023)

Опробация 17 мая 2023 2 вариант
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14 & 5 = 11102& 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула ((x & 42 ≠ 0) /\ (x & 34 = 0)) → ¬ (x & А = 0) тождественно истинна (т.е. принимает значение 1) при любом неотрицательном целом значении переменной х?
def f(x): return (((x & 42 != 0) and (x & 34 == 0)) <= (x & a != 0)) for a in range(1, 1000): if all(f(x) for x in range(1, 1000)): print(a) break

Для какого наименьшего натурального числа А формула тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?

Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5 = 11102&01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула x&25 ≠ 0 → (x&17 = 0 → x&А ≠ 0) тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
for A in range(32): B = True for x in range(32): if ((x&25==0) or (x&17!=0) or (x&A!=0))==0: B=False if B: print(A) break
Ответ: 8

Решу ЕГЭ №1 Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14 & 5 = 11102 & 01012 = 01002 = 4. Для какого наименьшего неотрицательного целого числа А формула x & 29 ≠ 0 → (x & 17 = 0 → x & А ≠ 0) тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?
for a in range(0, 1000): k = 0 for x in range(0, 1000): if (x & 29 != 0) <= ((x & 17 == 0) <= (x & a != 0)): k += 1 if k == 1000: print(a) break
Ответ: 12.

Программы для повторения