Презентация - Пирамида
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 98%
- Слайдов: 26
- Просмотров: 8601
- Скачиваний: 2343
- Размер: 1.38 MB
- Онлайн: Да
- Формат: ppt / pptx
Слайды и текст этой онлайн презентации
Слайд 1

Методическая разработка Савченко Е.М.
МОУ гимназия №1, г. Полярные Зори, Мурманской обл.
Геометрия 10
Пирамида
Геометрия 10
Пирамида
Слайд 2
А1
А2
Аn
Р
А3
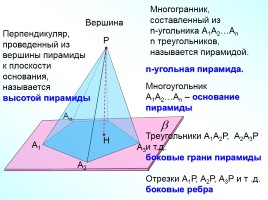
Многогранник, составленный из n-угольника А1А2…Аn n треугольников, называется пирамидой.
Вершина
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды
n-угольная пирамида. Многоугольник А1А2…Аn – основание пирамиды
Треугольники А1А2Р, А2А3Р и т.д. боковые грани пирамиды Отрезки А1Р, А2Р, А3Р и т .д. боковые ребра
А2
Аn
Р
А3
Многогранник, составленный из n-угольника А1А2…Аn n треугольников, называется пирамидой.
Вершина
Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется высотой пирамиды
n-угольная пирамида. Многоугольник А1А2…Аn – основание пирамиды
Треугольники А1А2Р, А2А3Р и т.д. боковые грани пирамиды Отрезки А1Р, А2Р, А3Р и т .д. боковые ребра
Слайд 3
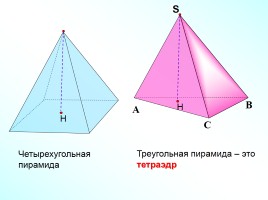
Треугольная пирамида – это
тетраэдр
Четырехугольная пирамида
Четырехугольная пирамида
Слайд 4
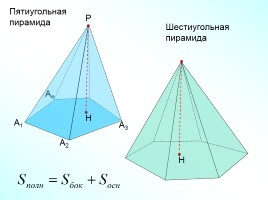
Пятиугольная
пирамида
А1
А2
Аn
Р
А3
Шестиугольная пирамида
А1
А2
Аn
Р
А3
Шестиугольная пирамида
Слайд 5
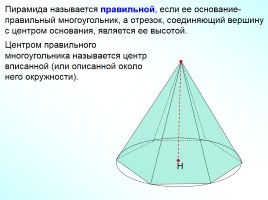
Пирамида называется правильной, если ее основание- правильный многоугольник, а отрезок, соединяющий вершину с центром основания, является ее высотой.
Центром правильного многоугольника называется центр вписанной (или описанной около него окружности).
Центром правильного многоугольника называется центр вписанной (или описанной около него окружности).
Слайд 6
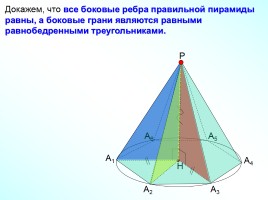
Докажем, что все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
А1
А2
А3
А4
А5
А6
Р
А1
А2
А3
А4
А5
А6
Р
Слайд 7
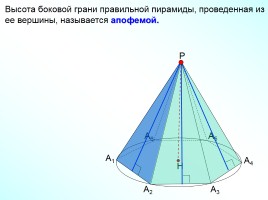
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
А1
А2
А3
А4
А5
А6
Р
А1
А2
А3
А4
А5
А6
Р
Слайд 8
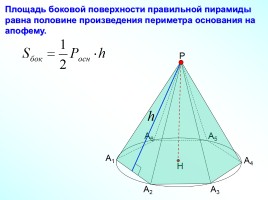
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
А1
А2
А3
А4
А5
А6
Р
А1
А2
А3
А4
А5
А6
Р
Слайд 9
С
А
В
Н
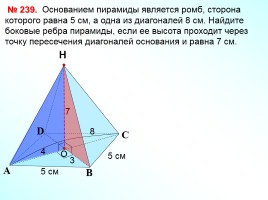
№ 239. Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей 8 см. Найдите боковые ребра пирамиды, если ее высота проходит через точку пересечения диагоналей основания и равна 7 см.
O
D
5 см
5 см
7
4
3
А
В
Н
№ 239. Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей 8 см. Найдите боковые ребра пирамиды, если ее высота проходит через точку пересечения диагоналей основания и равна 7 см.
O
D
5 см
5 см
7
4
3
Слайд 10
С
В
А
D
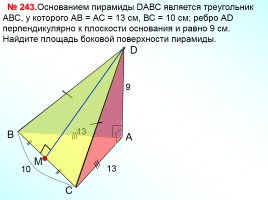
Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13 см, ВС = 10 см; ребро АD перпендикулярно к плоскости основания и равно 9 см. Найдите площадь боковой поверхности пирамиды.
№ 243.
13
9
10
13
В
А
D
Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13 см, ВС = 10 см; ребро АD перпендикулярно к плоскости основания и равно 9 см. Найдите площадь боковой поверхности пирамиды.
№ 243.
13
9
10
13
Слайд 11
С
В
А
D
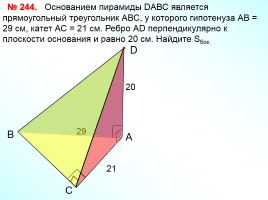
Основанием пирамиды DАВС является прямоугольный треугольник АВС, у которого гипотенуза АВ = 29 см, катет АС = 21 см. Ребро АD перпендикулярно к плоскости основания и равно 20 см. Найдите Sбок.
№ 244.
21
20
29
В
А
D
Основанием пирамиды DАВС является прямоугольный треугольник АВС, у которого гипотенуза АВ = 29 см, катет АС = 21 см. Ребро АD перпендикулярно к плоскости основания и равно 20 см. Найдите Sбок.
№ 244.
21
20
29
Слайд 12
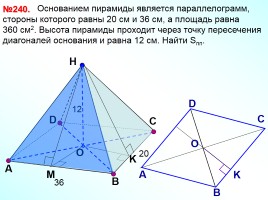
Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см, а площадь равна
360 см2. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 см. Найти Sпп.
D
Н
O
А
B
№240.
С
20
36
12
D
Н
O
А
B
№240.
С
20
36
12
Слайд 13
D
Н
O
А
B
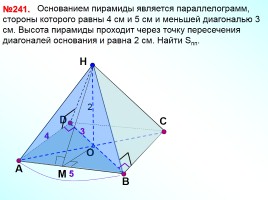
№241.
С
4
5
2
3
Основанием пирамиды является параллелограмм, стороны которого равны 4 см и 5 см и меньшей диагональю 3 см. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 см. Найти Sпп.
Н
O
А
B
№241.
С
4
5
2
3
Основанием пирамиды является параллелограмм, стороны которого равны 4 см и 5 см и меньшей диагональю 3 см. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 см. Найти Sпп.
Слайд 14
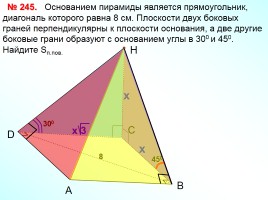
Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 300 и 450. Найдите Sп.пов.
А
D
Н
№ 245.
x
В
450
8
С
300
x
А
D
Н
№ 245.
x
В
450
8
С
300
x
Слайд 15
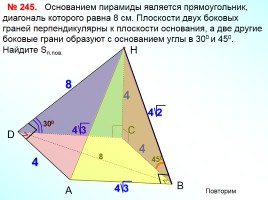
Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 300 и 450. Найдите Sп.пов.
А
D
Н
№ 245.
4
В
450
8
С
300
4
4
8
Повторим
А
D
Н
№ 245.
4
В
450
8
С
300
4
4
8
Повторим
Слайд 16
А
В
С
D
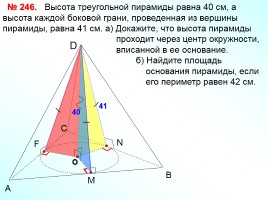
Высота треугольной пирамиды равна 40 см, а высота каждой боковой грани, проведенная из вершины пирамиды, равна 41 см. а) Докажите, что высота пирамиды проходит через центр окружности, вписанной в ее основание. б) Найдите площадь основания пирамиды, если его периметр равен 42 см.
№ 246.
В
С
D
Высота треугольной пирамиды равна 40 см, а высота каждой боковой грани, проведенная из вершины пирамиды, равна 41 см. а) Докажите, что высота пирамиды проходит через центр окружности, вписанной в ее основание. б) Найдите площадь основания пирамиды, если его периметр равен 42 см.
№ 246.
Слайд 17
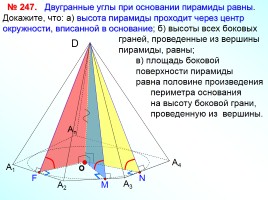
Двугранные углы при основании пирамиды равны. Докажите, что: а) высота пирамиды проходит через центр окружности, вписанной в основание; б) высоты всех боковых
граней, проведенные из вершины
пирамиды, равны;
в) площадь боковой
поверхности пирамиды
равна половине произведения
периметра основания
на высоту боковой грани,
проведенную из вершины.
№ 247.
А1
Аn
D
А2
А3
А4
№ 247.
А1
Аn
D
А2
А3
А4
Слайд 18
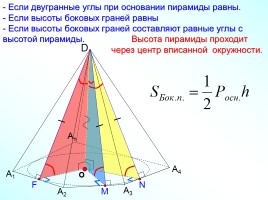
- Если двугранные углы при основании пирамиды равны.
Если высоты боковых граней равны
Если высоты боковых граней составляют равные углы с высотой пирамиды. Высота пирамиды проходит
через центр вписанной окружности.
А1
Аn
D
А2
А3
А4
А1
Аn
D
А2
А3
А4
Слайд 19
А
В
С
D
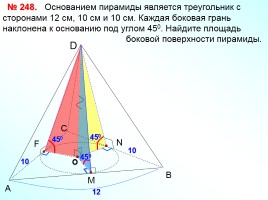
Основанием пирамиды является треугольник с сторонами 12 см, 10 см и 10 см. Каждая боковая грань наклонена к основанию под углом 450. Найдите площадь боковой поверхности пирамиды.
№ 248.
12
10
10
В
С
D
Основанием пирамиды является треугольник с сторонами 12 см, 10 см и 10 см. Каждая боковая грань наклонена к основанию под углом 450. Найдите площадь боковой поверхности пирамиды.
№ 248.
12
10
10
Слайд 20
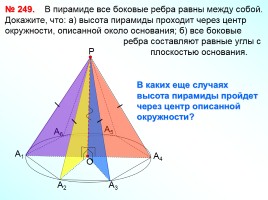
№ 249. В пирамиде все боковые ребра равны между собой. Докажите, что: а) высота пирамиды проходит через центр окружности, описанной около основания; б) все боковые
ребра составляют равные углы с
плоскостью основания.
А1
А2
А3
А4
А5
А6
Р
В каких еще случаях высота пирамиды пройдет через центр описанной окружности?
А1
А2
А3
А4
А5
А6
Р
В каких еще случаях высота пирамиды пройдет через центр описанной окружности?
Слайд 21
А1
А2
А3
А4
А5
А6
Р
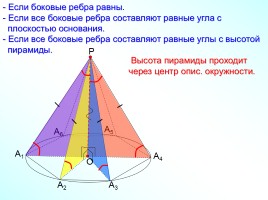
- Если боковые ребра равны. Если все боковые ребра составляют равные угла с плоскостью основания. Если все боковые ребра составляют равные углы с высотой пирамиды. Высота пирамиды проходит через центр опис. окружности.
А2
А3
А4
А5
А6
Р
- Если боковые ребра равны. Если все боковые ребра составляют равные угла с плоскостью основания. Если все боковые ребра составляют равные углы с высотой пирамиды. Высота пирамиды проходит через центр опис. окружности.
Слайд 22
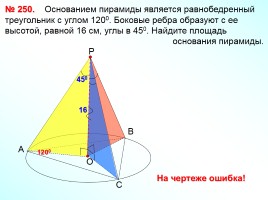
№ 250. Основанием пирамиды является равнобедренный треугольник с углом 1200. Боковые ребра образуют с ее высотой, равной 16 см, углы в 450. Найдите площадь
основания пирамиды.
А
В
С
Р
1200
450
16
На чертеже ошибка!
А
В
С
Р
1200
450
16
На чертеже ошибка!
Слайд 23
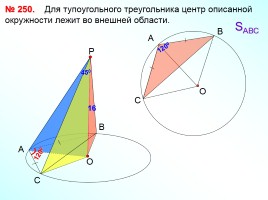
№ 250. Для тупоугольного треугольника центр описанной окружности лежит во внешней области.
А
В
С
Р
1200
SАВС
А
В
С
Р
1200
SАВС
Слайд 24
А
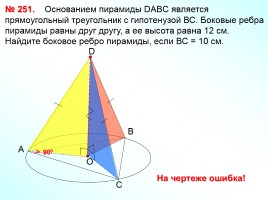
№ 251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой ВС. Боковые ребра пирамиды равны друг другу, а ее высота равна 12 см. Найдите боковое ребро пирамиды, если ВС = 10 см.
В
С
D
900
На чертеже ошибка!
№ 251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой ВС. Боковые ребра пирамиды равны друг другу, а ее высота равна 12 см. Найдите боковое ребро пирамиды, если ВС = 10 см.
В
С
D
900
На чертеже ошибка!
Слайд 25
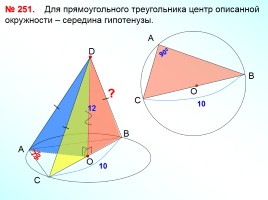
№ 251. Для прямоугольного треугольника центр описанной окружности – середина гипотенузы.
А
В
С
D
900
10
А
В
С
D
900
10
Слайд 26
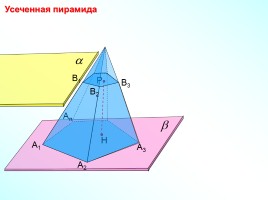
А1
А2
Аn
А3
Усеченная пирамида
А2
Аn
А3
Усеченная пирамида
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.







