Презентация - Призма (решение задач)

ПРИЗМА. Решение задач
Жукова Н.П. МОУ Гимназия №4 г. Можайск

Вопросы по теме «ПРИЗМА»
1 2 3
4 5 6
7 8 9

Какой многогранник называется призмой?

Является ли прямоугольный параллелепипед призмой?

Какими отрезками являются боковые ребра призмы?

Какая призма называется прямой ? правильной?

Может ли в основании правильной призмы лежать равнобедренный треугольник ? Ромб?

В каком случае высота призмы равна ее боковому ребру?

Чему равен квадрат диагонали прямоугольного параллелепипеда?

Чему равна боковая поверхность прямой призмы?

Как найти полную поверхность призмы?

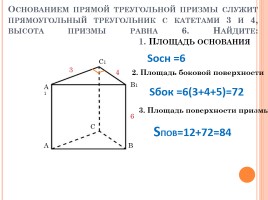
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4, высота призмы равна 6. Найдите: 1. Площадь основания
3
4
6
А
С
В
А1
С1
В1
Sосн =6
Sбок =6(3+4+5)=72
2. Площадь боковой поверхности
3. Площадь поверхности призмы
SПОВ=12+72=84

1200
А1
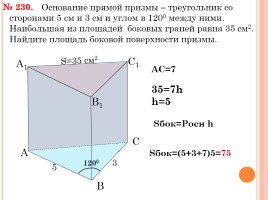
Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом в 1200 между ними. Наибольшая из площадей боковых граней равна 35 см2. Найдите площадь боковой поверхности призмы.
№ 230.
А
В
С
С1
В1
3
5
S=35 см2
АС=7
35=7h h=5
Sбок=Росн h
Sбок=(5+3+7)5=75

В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите площадь его боковой поверхности
В
С
А1
D1
С1
В1
13
D
А
12 см
5 см
13
Sосн = 60
Sбок = РоснН
Sбок = 442

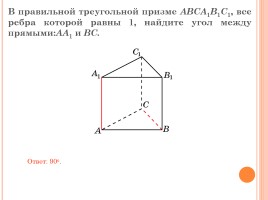
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между прямыми:AA1 и BC.
Ответ: 90o.

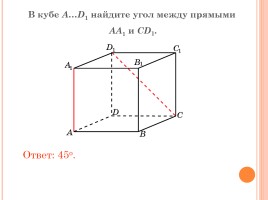
В кубе A…D1 найдите угол между прямыми AA1 и CD1.
Ответ: 45o.

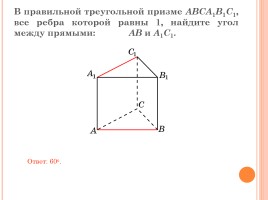
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите угол между прямыми: AB и A1C1.
Ответ: 60o.

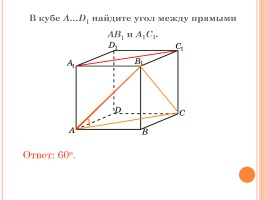
В кубе A…D1 найдите угол между прямыми AB1 и A1C1.
Ответ: 60o.

В III веке до н.э. был построен маяк, чтобы корабли могли благополучно миновать рифы на пути в александрийскую бухту. Ночью им помогало в этом отражение языков пламени, а днем - столб дыма. Это был первый в мире маяк, и простоял он 1500 лет
Фаросский маяк состоял из трех мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню. Верхняя башня формой напоминала цилиндр, в котором горел огонь, помогавший кораблям благополучно достигнуть бухты. На вершине башни стояла статуя Зевса Спасителя. Общая высота маяка составляла 117 метров.
Александрийский маяк

По местам наших экскурсий…
"Се памятник двух царств, Обоим им приличный, На мраморном низу Воздвигнут верх кирпичный". 

Исаакиевский собор (г. Санкт-Петербург)

ГРАНД МАКЕТ РОССИИ

ПРИЗМЫ вокруг нас
Кристаллография
Г.Можайск

КРИСТАЛЛОГРАФИЯ
Оказывается, что кристаллы кальцита, сколько их не дроби на более мелкие части, всегда распадаются на осколки, имеющие форму параллелепипеда.

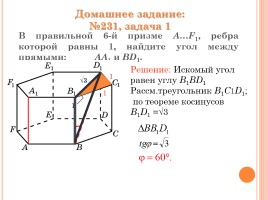
В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AA1 и BD1.
Решение: Искомый угол равен углу B1BD1 Рассм.треугольник B1С1D1; по теореме косинусов B1D1 =√3
1
1
1
√3

Домашнее задание: №231, задача 1