Презентация - Различные способы решения квадратных уравнений

. Выполнила: Алексеева Елена, ученица 10 класса. Руководитель: Алексеева Мария Ананьевна, учитель математики.
Различные способы решения квадратных уравнений.

Цель моей работы: рассмотреть и систематизировать различные способы решения квадратных уравнений. Задачи: Изучить литературу по теме исследования. Провести опрос и систематизировать материалы. Сделать выводы. Методы: поиск, анализ, опрос, систематизация. Объект исследования: алгебра. Предмет исследования: квадратные уравнения. Актуальность моей темы состоит в том, что учащиеся с 8-11 класс практически ежедневно сталкиваются с решением квадратного уравнения, и стараются как можно быстрее найти его корни, чтобы решить поставленные задачи.

Опрос-анкета. 1)Умеете, ли вы решать квадратные уравнения? А)Да Б)Нет 2)Возникают ли трудности у вас при решении квадратного уравнения? А)Да Б)Нет 3)Часто ли вы решаете квадратные уравнения. А)Да Б)Нет 4)Столько способов решения квадратного уравнения вы знаете? Ответ: 5)Какой способ решения квадратных уравнений вы используете чаще других? Ответ:

Способы решения квадратных уравнений. 1. СПОСОБ: Разложение левой части уравнения на множители. Решим уравнение х2 + 10х - 24 = 0. Разложим левую часть на множители: х2 + 10х - 24 = х2 + 12х - 2х - 24 = =х(х + 12) - 2(х + 12) = (х + 12)(х - 2). Следовательно, уравнение можно переписать так: (х + 12)(х - 2) = 0 Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = - 12. Это означает, что число 2 и - 12 являются корнями уравнения х2 + 10х - 24 = 0. Ответ: х 1 =−12; х 2 =2.

2. СПОСОБ: Метод выделения полного квадрата. Решим уравнение х2 + 10х - 24 = 0. Выделим в левой части полный квадрат. Для этого запишем выражение х2 + 10х в следующем виде: х2 + 10х = х2 + 2• х • 5. В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 5. По этому чтобы получить полный квадрат, нужно прибавить 52, получим х2 + 2• х • 5 + 52 = (х + 5)2. Преобразуем теперь левую часть уравнения х2 + 10х - 24 = 0, прибавляя к ней и вычитая 52. Имеем: х2 + 10х - 24 = х2 + 2• х • 5 + 52 - 52 - 24 = (х + 5)2 - 25 - 24 = (х + 5)2 - 49. Таким образом, данное уравнение можно записать так: (х + 5)2 - 49 =0, (х + 5)2 = 49. Следовательно, х + 5 - 7 = 0, х1 = 2, или х + 5 = -7, х2 = -12. Ответ: х 1 =−12; х 2 =2.

3. СПОСОБ: Решение квадратных уравнений по формуле. Решим уравнение: х2 + 10х -24 = 0, где а = 1, b = 10, с = -24, D = b2 - 4ac = 102 - 4 • 1 • (-24) = 100+96 =196= 14 2 , Таким образом, в случае положительного дискриминанта, т.е. при b2 - 4ac >0 , уравнение ах2 + bх + с = 0 имеет два различных корня. х 1 = −????+ ???? 2???? = −10+14 2×1 = 4 2 =2; х 2 = −????− ???? 2???? = −10−14 2×1 = −24 2 =−12. Ответ: х 1 =−12; х 2 =2.

4. СПОСОБ: Решение уравнений с использованием теоремы Виета. Как известно, приведенное квадратное уравнение имеет вид х2 + px + q = 0 (1). Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид x1 x2 = q, x1 + x2 = - p Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней). а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р > 0, то оба корня положительны. б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 . Решим уравнение x2 + 10x - 24 = 0, где х 1 × х 2 =−24 и х 1 + х 2 =−10, так как q = -24 < 0 и p = 10>0. Значит х 1 =−12; х 2 =2. Ответ: х 1 =−12; х 2 =2.

5. СПОСОБ: Решение уравнений способом «переброски». Рассмотрим квадратное уравнение ах2 + bх + с = 0, где а ≠ 0. Умножая обе его части на а, получаем уравнение а2х2 + аbх + ас = 0. Пусть ах = у, откуда х = ???? ???? ; тогда приходим к уравнению у2 + by + ас = 0, равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = ???? 1 ???? и х1 = ???? 2 ???? . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат. Решим уравнение 2х2 – 11х + 15 = 0. Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение у2 – 11у + 30 = 0. Согласно теореме Виета у1 = 5 х1 = 5 2 x1 = 2,5 у2 = 6 x2 = 6 2 x2 = 3. Ответ: х 1 =2,5; х 2 =3.

  6. СПОСОБ: Свойства коэффициентов квадратного уравнения. А. Пусть дано квадратное уравнение ах2 + bх + с = 0, где а ≠ 0. 1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1, х2 = ???? ???? . Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение x2 + b/a • x + c/a = 0. Согласно теореме Виета x1 + x2 = - b/a, x1x2 = 1• c/a. По условию а – b + с = 0, откуда b = а + с. Таким образом, x1 + x2 = - а + b/a= -1 – c/a, x1x2 = - 1• ( - c/a), т.е. х1 = -1 и х2 = c/a, что м требовалось доказать. Решим уравнение 345х2 – 137х – 208 = 0. Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то х1 = 1, х2 = ???? ???? =− 208 345 . Ответ: х1 = 1, х2 =− 208 345 .  

Б. Приведенное уравнение х2 + рх + q= 0 совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней    принимает вид:  Формулу (3) особенно удобно использовать, когда р — четное число. Решим уравнение х2 + 10х -24 = 0. Имеем: х 1,2 =−5± (5 2) − −24 , х 1 =−12; х 2 =2. Ответ: х 1 =−12; х 2 =2.

7. СПОСОБ: Графическое решение квадратного уравнения. Если в уравнении х2 + px + q = 0 перенести второй и третий члены в правую часть, то получим х2 = - px - q. Построим графики зависимости у = х2 и у = - px - q. График первой зависимости - парабола, проходящая через начало координат. График второй зависимости - прямая (рис.1). Возможны следующие случаи: - прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квад- ратного уравнения; - прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение; - прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней. Решим графически уравнение х2 - 3х - 4 = 0 (рис. 2). Решение. Запишем уравнение в виде х2 = 3х + 4. Построим параболу у = х2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М (0; 4) и N (3; 13). Прямая и парабола пересекаются в двух точках А и В с абсциссами х1 = - 1 и х2 = 4. Ответ: х1 = - 1; х2 = 4.

8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки. Предлагаю следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис. 5). Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 - корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a. Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому Итак: 1) построим точки (центр окружности) и A(0; 1); 2) проведем окружность с радиусом SA; 3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая. 1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х1; 0) и D(х2; 0), где х1 и х2 - корни квадратного уравнения ах2 + bх + с = 0. 2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 - корень квадратного уравнения. 3) Радиус окружности меньше ординаты центра   окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.

Решим уравнение х2 - 2х - 3 = 0 (рис. 7). Решение. Определим координаты точки центра окружности по формулам: Проведем окружность радиуса SA, где А (0; 1). Ответ: х1 = - 1; х2 = 3

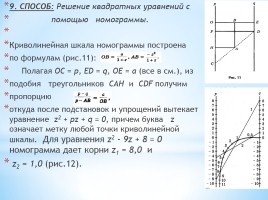
9. СПОСОБ: Решение квадратных уравнений с помощью номограммы. Криволинейная шкала номограммы построена по формулам (рис.11): Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию откуда после подстановок и упрощений вытекает уравнение z2 + pz + q = 0, причем буква z означает метку любой точки криволинейной шкалы. Для уравнения z2 - 9z + 8 = 0 номограмма дает корни z1 = 8,0 и z2 = 1,0 (рис.12).

Заключение Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Эти знания могут пригодиться нам на протяжении всей жизни. Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников. Моя работа дает возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.

Список использованной литературы: 1. Алгебра 8 кл: Учебн. пособие для учащихся школ и классов с углубленным изучением математики /Н.Я.Виленкин, А.Н.Виленкин, Г.С.Сурвилло и др., Под ред Н.Я.Виленкина.-М.:Просвещение, 1997. 2.Морткович А.Г. Алгебра 8 кл.: Учеб. Пособие для общеобразоват. Учреждений.-М.:Мнемозина, 2003. 3.Сборник задач по математике для поступающих в вузы: Учеб.Пособие/В.К. Егерев, Б.А.Кордемский, В.В.Зайцев и др; Под ред. М.И.Сканави-М.:СТОЛОТИЕ, 1997 4.Алимов Ш.А., Ильин В.А. и др. Алгебра, 6-8. Пробный учебник для 6-8 классовой средней школы. - М., Просвещение, 1981. 5. Брадис В.М. Четырехзначные математические таблицы для средней школы. Изд. 57-е. - М., Просвещение, 1990. С. 83. 6. Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. - М., высшая школа, 1969. 7. Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. - М., Просвещение, 1987. 8. Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. - М., Квант, № 4/82. С. 34. 9. Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. - 4-е, дополн. - М., Высшая школа, 1973. 10. Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. - М., Просвещение, 1970.

Спасибо за внимание.