Слайды и текст этой онлайн презентации
Слайд 1
Угол между плоскостями
Решение задач уровня С.
Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа №85
г.о. Тольятти
учитель математики высшей категории Баленко Тамара Борисовна
Слайд 2
Данная тема актуальна, так как подобные задачи требуют развитого абстрактного мышления. Задачи, представленные ниже, чаще всего вызывают затруднения при решении у учащихся. Наглядное решение позволяет лучше усвоить приемы решения таких задач.
Нахождение угла между скрещивающимися прямыми и угла между плоскостями
Слайд 3
Аргументы
1. Определение куба.
2. Определение правильной призмы.
3. Свойства правильной призмы.
4. Свойство средней линии треугольника.
5. Признак параллельности плоскостей.
6. Определение угла между плоскостями.
7. Линейный угол двугранного угла.
8. Теорема Пифагора.
9. Теорема косинусов.
Слайд 4
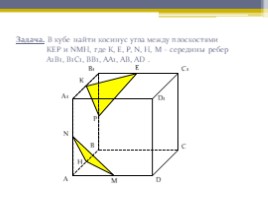
Задача. В кубе найти косинус угла между плоскостями КЕР и NМН, где К, Е, Р, N, Н, М – середины ребер А1В1, В1С1, ВВ1, АА1, АВ, АD .
А
А1
В1
С1
С
D
D1
В
К
Е
Р
N
М
H
Слайд 5
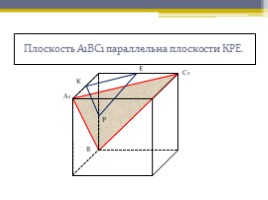
Плоскость А1ВС1 параллельна плоскости КРЕ.
К
Е
Р
А1
В
С1
Слайд 6
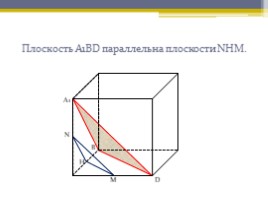
Плоскость А1ВD параллельна плоскости NНМ.
А1
В
D
Н
М
N
Слайд 7
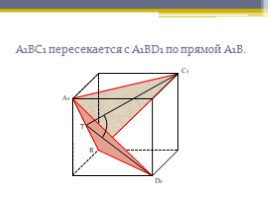
А1ВС1 пересекается с А1ВD1 по прямой А1В.
А1
С1
Т
D1
В
Слайд 8
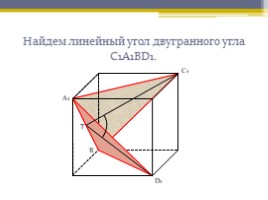
Найдем линейный угол двугранного угла С1А1ВD1.
А1
С1
Т
D1
В
Слайд 9
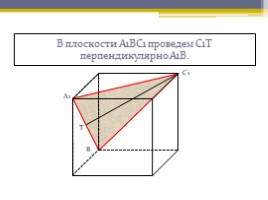
В плоскости А1ВС1 проведем С1Т перпендикулярно А1В.
А1
В
С1
Т
Слайд 10
В плоскости А1ВD проведем DТ перпендикулярно А1В
А1
В
D
Т
Слайд 11
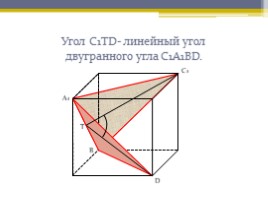
Угол С1ТD- линейный угол двугранного угла С1А1ВD.
А1
С1
Т
D
В
Слайд 12
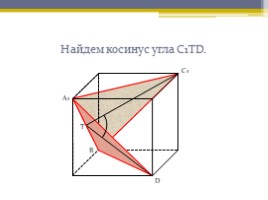
Найдем косинус угла С1ТD.
А1
С1
Т
D
В
Слайд 13
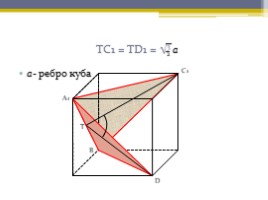
ТС1 = ТD1 = √3
а- ребро куба
А1
С1
Т
D
В
2
а
Слайд 14
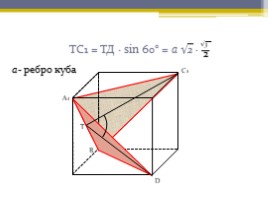
ТС1 = ТД · sin 60° = а √2 ·
А1
С1
Т
D
В
√3
2
а- ребро куба
Слайд 15
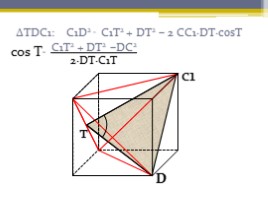
ΔTDC1: C1D2 ₌ C1T2 + DT2 – 2 CC1∙DT∙cosT C1T2 + DT2 –DC2
2∙DT∙C1T
cos T₌
т
с1
D
Слайд 16
Находим cos T:
сosT₌
₌
₌
Ответ:
.
.
Слайд 17
Спасибо за внимание.
 Решение задач по теме: «аксиомы стереометрии. Взаимное расположение прямых в пространстве. Угол между двумя прямыми". Геометрия 10 класс
Решение задач по теме: «аксиомы стереометрии. Взаимное расположение прямых в пространстве. Угол между двумя прямыми". Геометрия 10 класс Угол между лучами. Угол между прямыми в пространстве. Перпендикулярные прямые
Угол между лучами. Угол между прямыми в пространстве. Перпендикулярные прямые Международное уголовное право
Международное уголовное право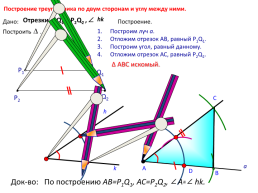 Построение треугольника по двум сторонам и углу между ними
Построение треугольника по двум сторонам и углу между ними Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Соотношения между сторонами и углами в прямоугольном треугольнике
Соотношения между сторонами и углами в прямоугольном треугольнике Угол между прямой и плоскостью
Угол между прямой и плоскостью