Презентация - Решение задач. Конус.

Тема урока: Конус. Решение задач.
Преподаватель математики: Лаптева Наталия Геннадьевна

Конус в переводе с греческого «konos» означает «сосновая шишка». С конусом люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287-212 гг. до н.э.) «О методе», в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа Демокриту (470-380 гг. до н.э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулу для вычисления объема пирамиды и конуса. Много сделала для геометрии школа Платона (428-348 гг. до н.э.). Платон был учеником Сократа (470-399 гг. до н.э.). Он в 387 г. до н.э. основал в Африке Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: «Пусть сюда не входит никто, не знающий геометрии». Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений. Большой трактат о конических сечениях был написан Аполлонием Пергским (260-170 гг. до н.э.) – учеником Евклида (III в. До н.э.), который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.

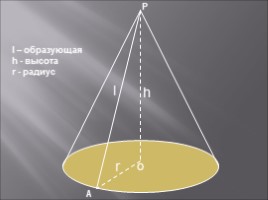
О
А
Р
h
r
l
l – образующая h - высота r - радиус

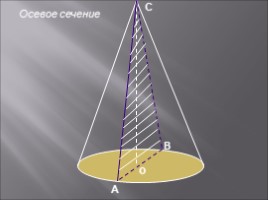
о
А
В
С
Осевое сечение

Площадь поверхности конуса

Теорема Пифагора
Квадрат гипотенузы равен сумме квадратов его катетов.
А
В
С

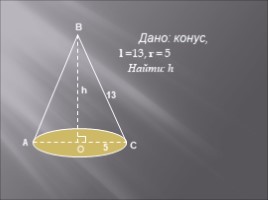
l =13, r = 5 Найти: h
О
А
С
В
h
13
5
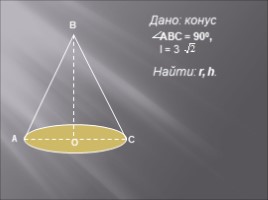
Дано: конус,

Найти: r, h.
АВС = 900, l = 3
А
В
С
О

Дано: конус

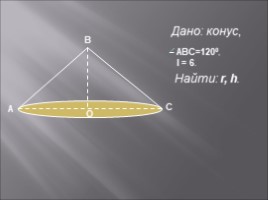
Найти: r, h.
АВС=1200, l = 6.
А
В
С
О
Дано: конус,

30 °
с
а
в
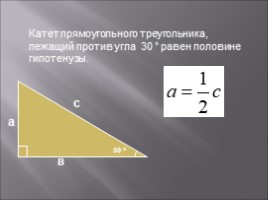
Катет прямоугольного треугольника, лежащий против угла 30 ° равен половине гипотенузы.

Решение задачи №1

Решение задачи №2

Решение задачи №3

Домашнее задание:
П.55,56 № 547, 548