Презентация - Конус. Решение задач

Конус. Решение задач

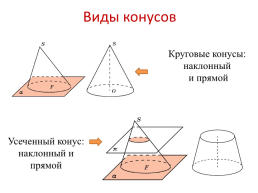
Виды конусов
Круговые конусы: наклонный и прямой
Усеченный конус: наклонный и прямой

Элементы конуса

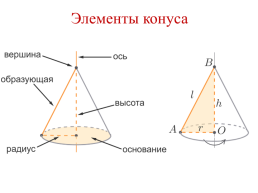
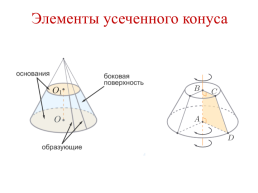
Элементы усеченного конуса

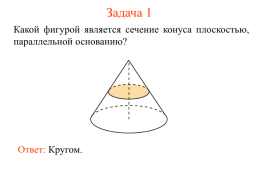
Задача 1
Какой фигурой является сечение конуса плоскостью, параллельной основанию?

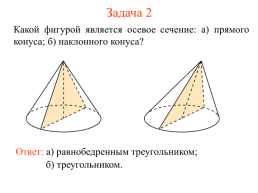
Задача 2
Какой фигурой является осевое сечение: а) прямого конуса; б) наклонного конуса?

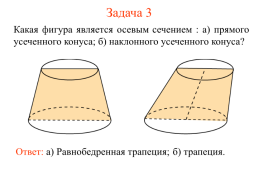
Задача 3
Какая фигура является осевым сечением : а) прямого усеченного конуса; б) наклонного усеченного конуса?

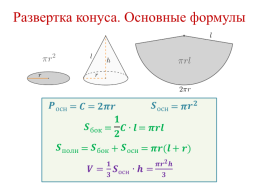
Развертка конуса. Основные формулы

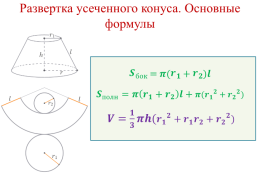
Развертка усеченного конуса. Основные формулы

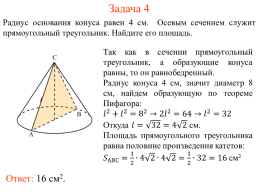
Задача 4
Радиус основания конуса равен 4 см. Осевым сечением служит прямоугольный треугольник. Найдите его площадь.
Так как в сечении прямоугольный треугольник, а образующие конуса равны, то он равнобедренный. Радиус конуса 4 см, значит диаметр 8 см, найдем образующую по теореме Пифагора: Откуда см. Площадь прямоугольного треугольника равна половине произведения катетов: см2
С
В
А
Ответ: 16 см2.

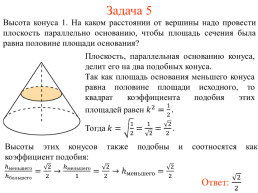
Задача 5
Высота конуса 1. На каком расстоянии от вершины надо провести плоскость параллельно основанию, чтобы площадь сечения была равна половине площади основания?
Плоскость, параллельная основанию конуса, делит его на два подобных конуса. Так как площадь основания меньшего конуса равна половине площади исходного, то квадрат коэффициента подобия этих площадей равен Тогда
Высоты этих конусов также подобны и соотносятся как коэффициент подобия:
Ответ:

Задача 6
Высота конуса равна 8 м, радиус основания - 6 м. Найдите образующую конуса. Его площадь поверхности и объем.
Найдем образующую по теореме Пифагора: м.
м2
l
м3
Ответ: 10 м, м2, м3.

Задача 7
Осевое сечение конуса - равносторонний треугольник со стороной 10 см. Найдите радиус основания и высоту конуса.
С
Так как в сечении равносторонний треугольник, то диаметр основания и образующие равны 10 см. Тогда радиус конуса см. Найдем высоту из ∆АСН по теореме Пифагора: см.
В
Н
А
Ответ: 5 см, см.

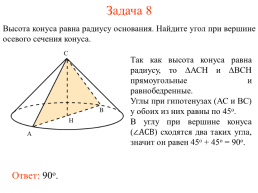
Задача 8
Высота конуса равна радиусу основания. Найдите угол при вершине осевого сечения конуса.
Так как высота конуса равна радиусу, то ∆АСН и ∆ВСН прямоугольные и равнобедренные. Углы при гипотенузах (АС и ВС) у обоих из них равны по 45о. В углу при вершине конуса () сходятся два таких угла, значит он равен 45о + 45о = 90о.
Ответ: 90о.

Задача 9
Образующая конуса равна 6 м и наклонена к плоскости основания под углом 60°. Найдите площадь полной поверхности и объем конуса.
Рассмотрим ∆АВН, он прямоугольный, в нем , тогда .
30о
Значит катет ВН (радиус конуса) равен половине гипотенузы 3 м.
Найдем высоту АН по теореме Пифагора: м.
Подставляем найденные величины в формулы площади и объема:
м2
м3
Ответ: 27 м2, м3.

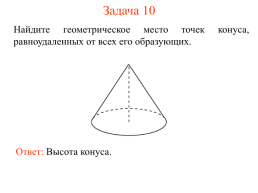
Задача 10
Найдите геометрическое место точек конуса, равноудаленных от всех его образующих.
Ответ: Высота конуса.

Задача 11
Радиусы оснований усеченного конуса равны 3 см и 6 см, образующая – 5 см. Найдите площадь полной поверхности и объем.
Рассмотрим трапецию ABCD, она прямоугольная. Проведем в ней высоту ВН. Тогда DH = 3 см, СН = 6 – 3 = 3 см.
Из треугольника ВСН по теореме Пифагора найдем высоту ВН, которая также является высотой усеченного конуса.
м.
Подставляем найденные величины в формулы площади и объема:
см2
см3
Ответ: см2, см3.

Задача 12
В сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда. Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
Высота конуса, образующегося из налитой воды равна половине высоты конуса, значит коэффициент подобия этих конусов . Отношение объемов подобных тел равно коэффициенту подобия в кубе, т. е.
Тогда осталось долить от всего объема конуса. Нам известно, что всего объема равна 25 мл. Значит, искомый объем жидкости равен 25 · 7 = 175 мл.
Ответ. 175 мл.

Задачи для самостоятельного решения
Найдите площадь полной поверхности и объем усеченного конуса, если он образован вращением прямоугольной трапеции с основаниями 9 и 14 см вокруг меньшей боковой стороны, равной 12 см. Объем первого конуса равен 60 м3. У второго конуса высота в три раза меньше, а радиус основания — в два раза больше, чем у первого. Найдите объем второго конуса. Радиус основания конуса равен 9 см. Найдите площадь полной поверхности и объем конуса, если осевое сечение конуса равносторонний треугольник. Площадь основания конуса равна 64π, а образующая — 10. Найдите площадь полной поверхности и объем конуса. В сосуд, имеющий форму конуса, налили 186 мл жидкости до трети высоты сосуда. Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?