Презентация - Цилиндр. Решение задач

Цилиндр. Решение задач

Элементы цилиндра

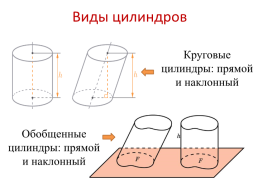
Виды цилиндров
Круговые цилиндры: прямой и наклонный
Обобщенные цилиндры: прямой и наклонный

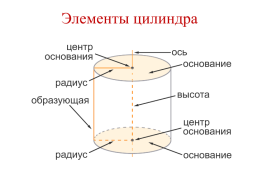
Развертка. Основные формулы

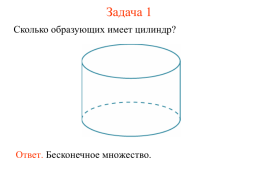
Задача 1
Сколько образующих имеет цилиндр?
Ответ. Бесконечное множество.

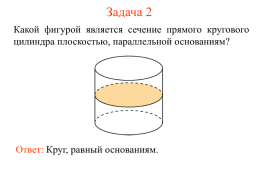
Задача 2
Какой фигурой является сечение прямого кругового цилиндра плоскостью, параллельной основаниям?

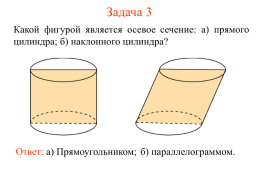
Задача 3
Какой фигурой является осевое сечение: а) прямого цилиндра; б) наклонного цилиндра?

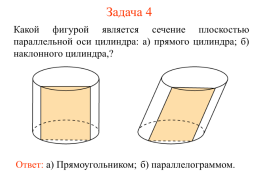
Задача 4
Какой фигурой является сечение плоскостью параллельной оси цилиндра: а) прямого цилиндра; б) наклонного цилиндра,?

Задача 5
Осевым сечением цилиндра является квадрат, площадь которого равна 4. Найдите радиус основания цилиндра, его высоту и образующую.
Осевым сечением цилиндра является квадрат, сторона которого равна одновременно высоте, образующей и диаметру основания.
Так как площадь этого квадрата равна 4, то его сторона равна .
Тогда высота и образующая цилиндра равны по 2, а радиус равен половине диаметра, то есть 1.
Ответ: 2, 2, 1.

Задача 6
Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен плоскостью параллельно оси так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси.
Обозначим квадрат сечения ABCD. Проведем ось цилиндра ОО1 и соединим точку О с А и В, тогда ОА = ОВ = 5 дм – радиусы основания.
Рассмотрим ∆AОB, он равнобедренный, АВ = 8 дм (по условию). Проведем в нем высоту ОН, которая также является медианой, тогда АН = ВН = 4 дм.
По теореме Пифагора найдем ОН (так как отрезок ОНАВ, он и будет расстоянием от сечения до оси).
дм.
Ответ: 3 дм.

Задача 7
Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой и полной поверхности цилиндра.
C– длина окружности основания.
Поэтому  Sбок = 2·3 = 6 кв. ед.
Откуда .
Значит кв. ед.
Получаем  Sполн кв. ед.
Ответ: .

Задача 8
Диаметр основания цилиндрического бака без крышки равен 1 м, высота равна 2 м. Сколько литровых банок краски потребуется для окрашивания бака изнутри и снаружи (толщиной пренебречь), если расход краски составляет 160 мл/м2.
Подставляем значения  Sбок = м2.
Тогда  Sосн = м2.
Sбака = м2.
м2; расход 160 мл/м2 = 0,16 л/м2.
л.
Значит потребуется 3 литровые банки краски.
Ответ: 3.

Задача 9
Диаметр основания наклонного кругового цилиндра равен 1. Образующая равна 2 и наклонена к плоскости основания под углом 60о. Найдите объем цилиндра.
Диаметр основания равен 1, значит радиус составляет 0,5, найдем :
кв. ед.
60о
Проведем высоту цилиндра.
Обозначим треугольник, образованный высотой, образующей и диаметром основания АВС. Он прямоугольный с углом A в 60о.
Через функцию синуса угла А найдем BC = h: .
Тогда куб. ед.
Ответ:

Задача 10
В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в  см3.
Обозначим объем жидкости , объем детали , а объем жидкости с деталью .
Тогда , откуда см2.
Площадь основания при погружении детали не изменилась, а высота увеличилась на 9 см, тогда см, значит, см3.
Отсюда см3.
Ответ. 1500.

Задача 11
Объем первого цилиндра равен 12 м3. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра.
Пусть объём первого цилиндра равен объем второго – , где r₁ и r₂ — радиусы оснований цилин­дров, h₁ и h₂ — их высоты.
Из условия: h₂ = 3h1, r2 = 0,5r1, тогда объем второго цилиндра равен:
Подставляем значение объема первого цилиндра: м3.
Ответ. 9.

Задачи для самостоятельного решения
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в  2  раза больше первого? Ответ выразите в см. Объем первого цилиндра равен 60 м3. У второго цилиндра высота в три раза меньше, а радиус основания — в два раза больше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах. Площадь боковой поверхности цилиндра равна 2π, а диаметр основания — 1. Найдите высоту цилиндра. Площадь боковой поверхности цилиндра равна 15π, а высота — 10. Найдите диаметр основания. В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.