Презентация - Сфера и шар. Решение задач

Сфера и шар. Решение задач

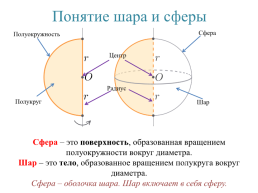
Понятие шара и сферы
Сфера
Полуокружность
Центр
Радиус
Полукруг
Шар
Сфера – это поверхность, образованная вращением полуокружности вокруг диаметра. Шар – это тело, образованное вращением полукруга вокруг диаметра. Сфера – оболочка шара. Шар включает в себя сферу.

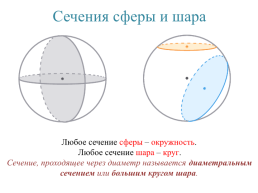
Сечения сферы и шара
Любое сечение сферы – окружность. Любое сечение шара – круг. Сечение, проходящее через диаметр называется диаметральным сечением или большим кругом шара.

Площадь сферы и объем шара
Для сферы и шара радиуса R справедливы формулы

Задача 1
Площадь большого круга шара равна 3 см2. Найдите площадь поверхности шара и его объем.
Так как большой круг шара – это его диаметральное сечение, то можем найти радиус шара: . см2. см3.
Ответ. 12 см2.

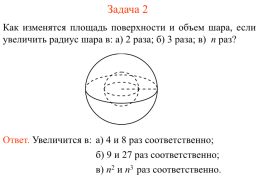
Задача 2
Как изменятся площадь поверхности и объем шара, если увеличить радиус шара в: а) 2 раза; б) 3 раза; в) n раз?
Ответ. Увеличится в:
а) 4 и 8 раз соответственно;
б) 9 и 27 раз соответственно;
в) n2 и n3 раз соответственно.

Задача 3
Площади поверхностей двух шаров относятся как 4 : 9. Найдите отношение их диаметров и объемов.
Площади подобных тел соотносятся как квадрат коэффициента подобия, значит: . Отношение диаметров равно коэффициенту подобия, т. к. диаметр – линейная величина, значит оно равно 2:3. Объем – величина кубическая, значит коэффициент подобия возводим в третью степень: . Тогда соотношение объемов 8:27.
Ответ: 2:3, 8:27.

Задача 4
Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Обозначим площадь меньшего шара S1, большего – S2. Тогда: кв. ед.; кв. ед.; кв. ед.
Пусть площадь искомого шара S3, получаем: .
Ответ. 10.

Задача 5
Сколько нужно взять шаров радиуса 2 см, чтобы сумма их объемов равнялась объему шара радиуса 6 см?
Коэффициент подобия радиусов этих шаров . Их объемы соотносятся как Тогда в шаре радиуса 6 см содержится 27 шаров радиуса 2 см.
Ответ: 27.

Задача 6
Объём шара равен 288 дм3. Найдите площадь его поверхности.
Из формулы объема шара найдем его радиус: . Тогда радиус равен дм. Подставляем в формулу площади:
дм2.
Ответ. дм2.

Задача 7
Радиусы трех шаров 3 см, 4 см и 5 см. Найдите радиус шара, объем которого равен сумме их объемов.
Обозначим объемы этих шаров V1, V2, V2: см3; см3; . Их суммарный объем см3. Найдем радиус см.
Ответ: 6 см.

Задача 8
Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите площадь поверхности и объем шара.
Проведем радиус шара ОМ = R.
Рассмотрим образовавшийся треугольник ОО1М.
Так как плоскость сечения перпендикулярна оси шара, то ∆ ОО1М прямоугольный, в котором известны два катета. Найдем гипотенузу по теореме Пифагора: см.
Подставляем найденный радиус в формулы площади и объема:
см2; см3.
Ответ. см2; см3.

Задача 9
Медный куб, ребро которого равно 10 см, переплавлен в шар. Найдите радиус шара. (Потерями металла при переплавке можно пренебречь.)
Объем куба равен его стороне в третьей степени: см3. Объем шара совпадает с объемом куба: см.
Ответ: 6,2 см.

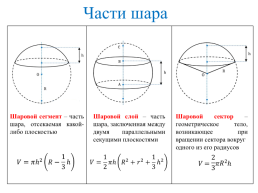
Части шара
..
Шаровой сектор – геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов
Шаровой сегмент – часть шара, отсекаемая какой-либо плоскостью
Шаровой слой – часть шара, заключенная между двумя параллельными секущими плоскостями

Задача 10
Какую часть объема шара составляет объем шарового сегмента, у которого высота равна 0,1 диаметра шара?
По условию нам известно, что высота сегмента , тогда от радиуса она составляет Подставим эту величину вместо h в формулу объема сегмента: .
Объем шара равен , найдем отношение их объемов:
.
Ответ. .

Задача 11
Найдите объем шарового слоя, если радиусы его оснований равны 3 см и 4 см, а радиус шара - 5 см. (Рассмотрите два случая.)
1 случай – основания слоя расположены по одну сторону от центра.
По условию нам известны радиусы оснований и , но чтобы найти объем нужно знать еще и высоту этого слоя h. Проведем 2 радиуса ОМ и ОК.
Рассмотрим образованные треугольники ∆ОО2М и ∆ОО1К. Оба они прямоугольные с гипотенузами равными 5 см и катетами 4 и 3 см соответственно. Найдем неизвестные катеты по теореме Пифагора: см, см. Высотой слоя будет отрезок см. Находим объем см3.

Задача 11 (продолжение)
Найдите объем шарового слоя, если радиусы его оснований равны 3 см и 4 см, а радиус шара - 5 см. (Рассмотрите два случая.)
2 случай – основания слоя расположены по разные стороны от центра.
Радиусы оснований те же и , нужно найти высоту h. Аналогично проведем радиусы ОМ и ОК.
Рассмотрим такие же треугольники ∆ОО2М и ∆ОО1К и применим в них теорему Пифагора: см, см. Как видим отрезки получились такие же, но высота такого слоя будет отличаться: см. Находим объем см3.
Ответ. см3 или см3.

Задача 12
Чему равен объем шарового сектора, если радиус окружности его сегмента равен 60 см, а радиус шара 75 см?
Чтобы найти высоту сегмента h, отметим радиусы шара ОМ и ОК. Рассмотрим ∆ОО1М. Он прямоугольный с гипотенузой ОМ = 75 см и катетом О1М = 60 см. Найдем ОО1 по теореме Пифагора: 5 см. Тогда О1К = h = ОК – ОО1 = 75 – 45 = 30 см.
Находим объем сектора см3.
Ответ. см3.

Задачи для самостоятельного решения
1) Однородный шар диаметром 3 см имеет массу 81 г. Чему равна масса и площадь поверхности шара из того же материала радиусом 5 см? 2) Стальной шар объемом 729 м3 переплавили в куб. Найдите площадь поверхности полученного куба. Потерями металла при переплавке пренебречь. 3) Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса в его основании составляет треть диаметра шара. 4) Радиус шарового сегмента равен 8 см, а радиус шара – 10 см. Найдите его объем. 5) По разные стороны от центра шара проведены два параллельных сечения с площадью 49π и 64π см2. Радиус шара равен 9 см. Определите объём получившегося шарового слоя.