Презентация - Основы логики: логические величины и формулы

Тема урока:
Основы логики: логические величины и формулы

1. Какой длины эта лента? 2. Прослушайте сообщение. 3. Париж – столица Англии. 4. Назовите устройство ввода информации. 5. Кто отсутствует? 6. Число 11 является простым. 7. Делайте утреннюю зарядку! 8. Сложите числа 2 и 5. 9. Некоторые медведи живут на севере.

Какие основные типы полей используются в базах данных? Числовой Годовой Символьный Логический Недельный «Дата»

Алгебра – это раздел математики, предназначенный для описания действий над переменными величинами, которые принято обозначать строчными латинскими буквами, например a, b, x, y и т.д. Логика (древнегреч. – слово logos, означает «мысль, понятие, рассуждение, закон») - наука о законах и формах мышления. Логическая переменная - это простое высказывание, содержащее только одну мысль. Её символическое обозначение – латинская буква (A, B, D, F …). Значениями логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 или 0). Логические операции – логические действия над высказываниями.
ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ

Аристотель (384-322 гг. до н.э.) – древнегреческий философ, основоположник логики. Книги: «Категории» «Первая аналитика» «Вторая аналитика» Исследовал различные формы рассуждений, ввел понятие силлогизма. Силлогизм - рассуждение, в котором из заданных двух суждений выводится третье. Декарт Рене (1596-1650, французский философ, математик) – рекомендовал в логике использовать математические методы.
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ

Лейбниц Готфрид Вильгельм (1646-1716, немецкий ученый и математик) – предложил использовать в логике математическую символику и впервые высказал мысль о возможности применения в ней двоичной системы счисления. Логика обретает символьный язык, конкретность законов, распространяется за рамки гуманитарных наук. Джордж Буль (1815-1864, английский математик-самоучка, основоположник математической логики) В 1846 году Джордж Буль подхватил идею Лейбница о создании логического универсального языка, подчиняющегося строгим математическим законам. Буль изобрел своеобразную алгебру – систему обозначений и правил, применимую к всевозможным объектам, от чисел и букв до предложений. Его именем она теперь и называется: алгебра Буля или булева алгебра.
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ

Логические функции ( логические формулы) – сложные логические выражения, образованные из простых и связанные логическими операциями И, ИЛИ, НЕ и др.) Высказывание «Все мышки и кошки с хвостами» является сложным и состоит из двух простых высказываний. А=«Все мышки с хвостами» и В=«Все кошки с хвостами» Его можно записать в виде логической функции, значение которой истинно: F(A,B)=A и B В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только ложно (0) или истинно (1).
АЛГЕБРА ВЫСКАЗЫВАНИЙ

1. Логическое умножение (к о н ъ ю н к ц и я)
2. Логическое сложение (д и з ъ ю н к ц и я)
3. Логическое отрицание (и н в е р с и я)

Синтаксис: F = A  B или F = A  B (F = A  B)
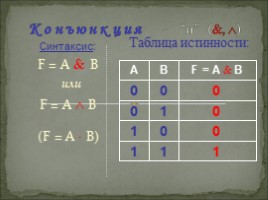
К о н ъ ю н к ц и я - “и” (, )
Таблица истинности:
1
0
0
0

Синтаксис: F = A  B (F = A + B)
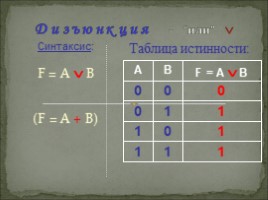
Д и з ъ ю н к ц и я - “или” 
Таблица истинности:
1
1
1
0

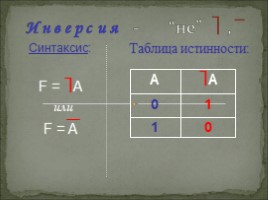
И н в е р с и я - “не”  , ¯
Синтаксис: F =  A или F = A
Таблица истинности:
0
1

Построение таблицы истинности сложных логических величин (ЛВ): 1) определить число простых ЛВ (n); 2) определить число строк в таблице истинности (q=2n); 3) записать все возможные значения простых ЛВ; 4) определить количество логических операций и их порядок; 5) записать логические операции в таблицу истинности и определить для каждой значение.
Алгоритм построения таблицы истинности

Построим таблицу истинности для выражения F=(AB)(AB)
A B AB A B AB (AB)(AB)

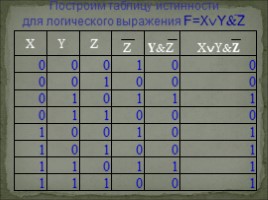
Построим таблицу истинности для логического выражения F=XYZ

Домашнее задание: § 13 Задание №5 выполнить в тетради