Презентация - Предмет и метод начертательной геометрии. Комплексный чертеж

План лекции 1 2 3 3 4 4 5

Начертательная геометрия- Раздел геометрии, в котором пространственные фигуры изучаются с помощью их изображений на плоскости Предметом н ачертательн ой геометри и являются: Способы построения изображени й пространственных ф о р м н а плоскости ; Исследование геометрических с войств объектов по их изображениям .

В начертательной геометрии используются графические методы решения задач

ЛИТЕРАТУРА Рябова И. П. Начертательная геометрия: Учебное пособие для всех форм обучения: Издательский центр ЮУр ГУ, 2014. Бударин О. С. Начертательная геометрия. Краткий курс: Учебное пособие. – СПб.: Издательство «Лань», 2019.

Историческая справка С древних времён человек старался сохранить образ увиденного. Наскальная живопись, украшенные рисунками стены жилища, посуда, предметы быта – первые тому свидетельства. Цивилизация развивалась, появились схемы и карты местности, изображение храмовых комплексов, жилых домов, военных сооружений, мостов, простых механизмов. Потребовалась выработка и первых общих правил представления пространственной информации на плоскости. Семь чудес света трудно представить без первых чертежей, рисунков и схем. Египетские, греческие и римские учёные, изучая перспективу, пытались выработать некие правила представления имеющейся информации.

Эпоха Возрождения вызвала расцвет архитектуры, скульптуры, живописи. Первые теоретические основы перспективы создал итальянский учёный Историческая справка Леон Баттиста Альберти (1 404 -1 472 )

Дополнил линейную перспективу учением "Об уменьшении цветов и отчётливости очертаний". Историческая справка Леонардо да Винчи (1 452 -1 519 )

Ввел метод координат французский архитектор Историческая справка Жерар Дезарг (1 593 -1 662 )

1 795 г. - появилась "Начертательная геометрия" Гаспара Монжа, им введено понятие «комплексный чертёж» и получены полностью обратимые изображения объемных (пространственных) объектов на плоскости. Историческая справка Гаспар Монж (1746 -1818) Основоположник начертательной геометрии -

Первый учебник по начертательной геометрии опубликован во Франции в 1798 г. Россия . Развитию начертательной геометрии способствовали А. Рублёв, Дионисий, архитекторы В. Баженов, А. Ворончихин; самоучки, механики-изобретатели И. Ползунов, И. Кулибин, И. Моторин и другие. 1810 г. – Карл Потье читает в С.-Петербурге первые лекции в Институте корпуса инженеров путей сообщения. 18 2 1 г. – Я. А. Севастьянов (1796-1849) издает оригинальный курс начертательной геометрии на русском языке. Историческая справка

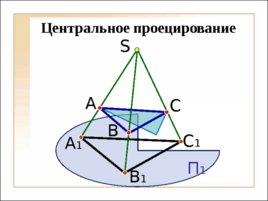
П 1 А 1 В 1 С 1 A C B S Центральное проецирование

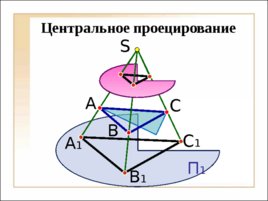
С 1 A B S А 1 C В 1 П 1 Центральное проецирование

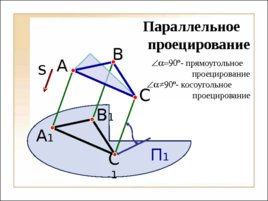
П 1 А 1 В 1 С 1 A C Паралле льное проецирование B º - прямоугольное проецирование º - косоугольное проецирование s

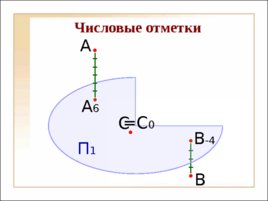
Числовые отметки А 6 A П 1 B C B -4 C 0

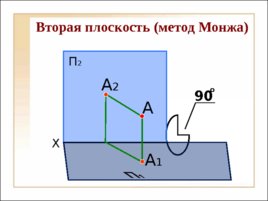
90 Вторая плоскость (метод Монжа) X П 2 А 1 А А 2

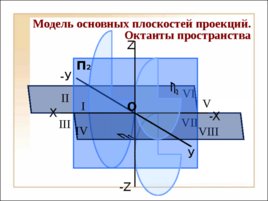
VIII VII VI -У X П 2 -X У Z - Z I II O IV V III Модель основных плоскостей проекций. Октанты пространства

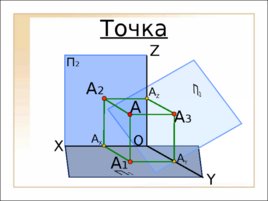
Точка O П 2 X Y Z А X А Y А 1 А А 2 А 3 А Z

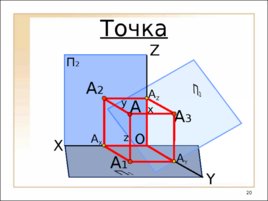
O X Y Z А X А Y А 1 А А 2 А 3 А Z x y z Точка П 2

Переход от пространственной модели к комплексному (ортогональному) чертежу

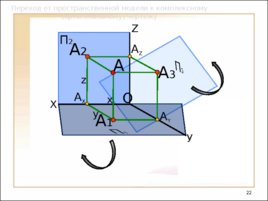
П 2 X Z А X А Y А 1 А А 2 А 3 А Z Переход от пространственной модели к комплексному (ортогональному) чертежу У O x y z

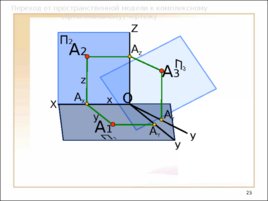
А Y А 1 А 3 Переход от пространственной модели к комплексному (ортогональному) чертежу А Y X У У А Z П 2 Z А 2 А X O x y z

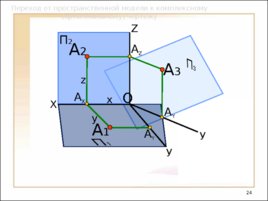
Переход от пространственной модели к комплексному (ортогональному) чертежу X У У O А Y А 1 А 3 А Y А X А Z П 2 Z А 2 x y z

Переход от пространственной модели к комплексному (ортогональному) чертежу X У У А Y А 1 А 3 А Y O А X А Z П 2 Z А 2 x y z

Переход от пространственной модели к комплексному (ортогональному) чертежу X У У А Y А 1 А 3 А Y O А X А Z П 2 Z А 2 x y z

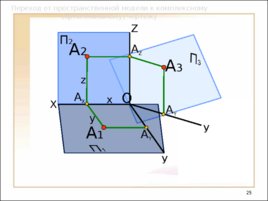
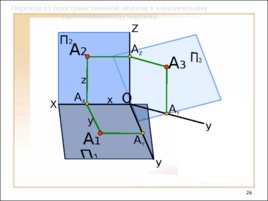
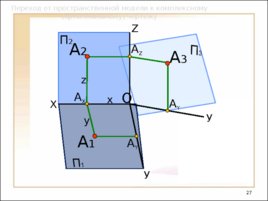
Переход от пространственной модели к комплексному (ортогональному) чертежу X У У А Y А 1 А 3 А Y А X А Z O П 2 Z А 2 x y z

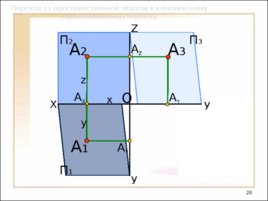
Переход от пространственной модели к комплексному (ортогональному) чертежу X У У А Y А 1 А Y А X А Z O П 2 Z А 2 П 1 П 3 А 3 x y z

1. Положение точки в п ространстве определяется тремя координатами A(x, y, z) ; 2. Положение проекции точки на плоскости проекций определяется двумя координатами А 1 (x, y), А 2 (x, z), А 3 (y, z) ; 3. Две проекции точки определяют ее положение в пространстве ; 4. Две проекции точки лежат на линии связи, перпендикуляр ной координатной оси .

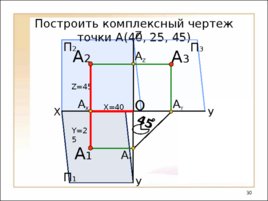
Построить комплексный чертеж точки А( 4 0, 25, 4 5 ) X У У А Y А 1 А Y А X А Z O П 2 Z А 2 П 1 П 3 А 3 X 4 0 Y 25 Z 45 45

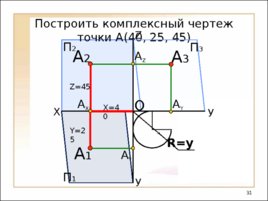
Построить комплексный чертеж точки А( 4 0, 25, 4 5 ) X У У А Y А 1 А Y А X А Z O П 2 Z А 2 П 1 П 3 А 3 X 4 0 Y 25 Z 45 R y

Линия – это множество всех п оследовательных положений двигающейся точки . Прямая линия – линия, о бразованная д вижением точки не меняющей своего н аправления . Прямая линия Прямая линия может быть зада на : 1. Двумя точками ей принадлежащими 2. Одной точкой и направлением линии

Прямая линия не параллельная и не перпендикулярная ни одной из плоскостей проекций называется – п рям ой общего положения. Прямая линия общего положения Замечание : На комплексном чертеже проекции прямой общего положения не параллельны и не перпендикулярны ни одной координатной оси.

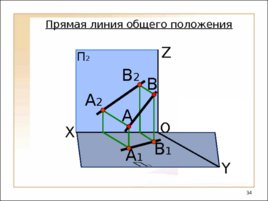
O П 2 X Y Z А 1 А А 2 Прямая линия общего положения В 1 В В 2

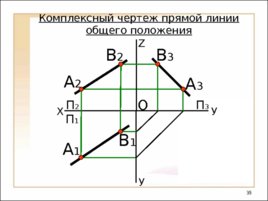
X У У А 1 O П 2 Z А 2 П 1 П 3 А 3 Комплексный чертеж прямой линии общего положения В 1 В 2 В 3

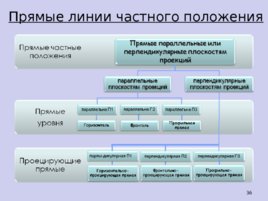
Прямые линии частного положения

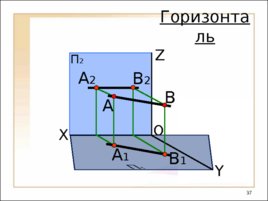
O П 2 X Y Z А 1 А А 2 Горизонталь В 1 В В 2

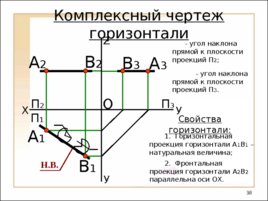
X У А 1 O П 2 Z А 2 П 1 П 3 А 3 Комплексный чертеж горизонтали В 1 В 2 В 3 Н. В. - угол наклона прямой к плоскости проекций П 2 ; - угол наклона прямой к плоскости проекций П 3 . Свойства горизонтали: 1. Горизонтальная проекция горизонтали А 1 В 1 – натуральная величина; У 2. Фронтальная проекция горизонтали А 2 В 2 параллельна оси ОХ.

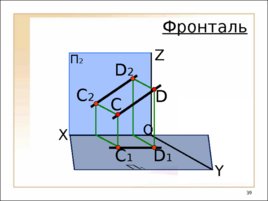
O П 2 X Y Z C 1 C С 2 Фронталь D 1 D D 2

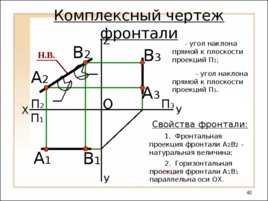
X У А 1 O П 2 Z А 2 П 1 П 3 А 3 Комплексный чертеж фронтали В 1 В 2 В 3 Н. В. - угол наклона прямой к плоскости проекций П 3 . Свойства фронтали: 1. Фронтальная проекция фронтали А 2 В 2 – натуральная величина; У 2. Горизонтальная проекция фронтали А 1 В 1 параллельна оси ОХ. - угол наклона прямой к плоскости проекций П 1 ;

Свойства проекций прямых уровня Если прямая параллельна плоскости проекций, то: на эту плоскость проецируются в натуральную величину сама прямая и углы наклона ее к двум другим плоскостям проекций; проекции прямой на две другие плоскости проекций, параллельны координатным осям.

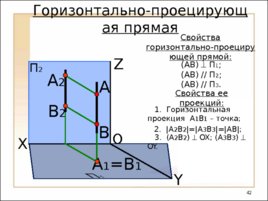
O П 2 X Y Z А А 2 А 1 В 1 В В 2 Горизонтально-проецирующая прямая Свойства горизонтально-проецирующей прямой: (АВ) П 1 ; (АВ) // П 2 ; (АВ) // П 3 . Свойства ее проекций: 1. Горизонтальная проекция А 1 В 1 – точка; 2. А 2 В 2 А 3 В 3 АВ ; 3 . ( А 2 В 2 ) OX; ( А 3 В 3 ) OY .

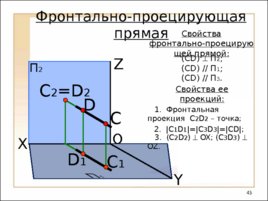
O П 2 X Y Z С С 1 D С 2 D 2 Фронтально-проецирующая прямая Свойства фронтально-проецирующей прямой: ( CD ) П 2 ; ( CD ) // П 1 ; ( CD ) // П 3 . Свойства ее проекций: 1. Фронтальная проекция С 2 D 2 – точка; 2. C 1 D 1 C 3 D 3 CD ; 3 . (C 2 D 2 ) OX; (C 3 D 3 ) OZ . D 1

Свойства проекций проецирующих прямых Если прямая перпендикулярна плоскости проекций, то: на эту плоскость она проецируются в точку; проекции прямой на две другие плоскости проекций проецируются в натуральную величину и перпендикулярны координатным осям.