Презентация - Функции y = tgx и y = ctgx, их свойства и графики

Функции y = tgx и y = ctgx, их свойства и графики

Определение
Тангенсом угла α называют число, равное отношению sin α к cos α, обозначают tg α, т. е.
Тангенс определён для всех углов α, кроме тех, для которых косинус равен нулю
Для любого угла α ≠ π/2 + πk, kЄZ существует, и притом единственный tg α

y
+ ∞
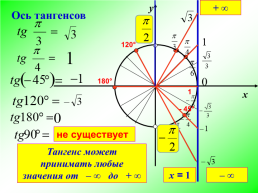
Ось тангенсов
120°
180°
x
- 45°
не существует
Тангенс может принимать любые значения от – ∞ до + ∞
х = 1
– ∞

Определение
Котангенсом угла α называют число, равное отношению cos α к sin α, обозначают сtg α, т. е.
Котангенс определён для всех углов α, кроме тех, для которых синус равен нулю
Для любого угла α ≠ πk, kЄZ существует, и притом единственный сtg α

Y
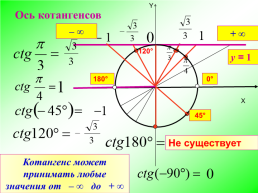
Ось котангенсов
– ∞
+ ∞
120°
у = 1
180°
0°
X
45°

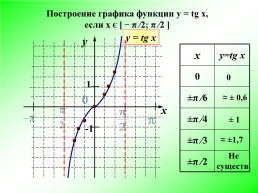
Построение графика функции y = tg x, если х Є [ ̶ π ∕2; π ∕2 ]
y
х.у=tg x
0.
±π ∕6.
±π ∕4.
±π ∕3.
±π ∕2.
≈ ± 0,6
x
± 1
-1
≈ ±1,7
Не существ.

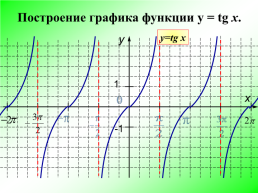
Построение графика функции y = tg x.
y
x
-1

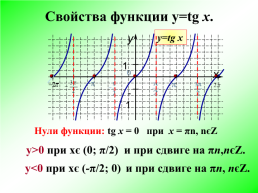
Свойства функции y=tg x.
Нули функции:
tg х = 0 при х = πn, nєZ
у>0 при хє (0; π/2) и при сдвиге на πn,nєZ.
у<0 при хє (-π/2; 0) и при сдвиге на πn, nєZ.

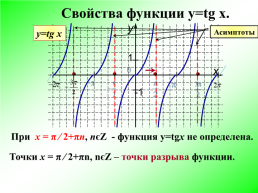
Свойства функции y=tg x.
При х = π ∕ 2+πn, nєZ - функция у=tgx не определена.
Точки х = π ∕ 2+πn, nєZ – точки разрыва функции.

Запишите все свойства функции y = tg x.
1. Область определения: 2. Множество значений функции: 3. Периодическая, Т= 4. Нечётная функция 5. Возрастает на всей области определения. 6. Нули функции у = 0 при х = 7. у > 0 при хє и при сдвиге на 8. у < 0 при хє и при сдвиге на 9. При х = - функция у = tgx не определена. Имеет точки разрыва графика

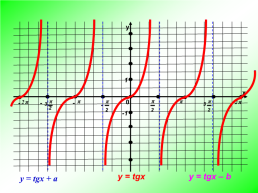
y = tgx
y = tgx – b
y = tgx + a

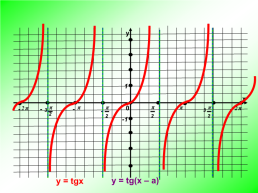
y = tg(x – a)
y = tgx

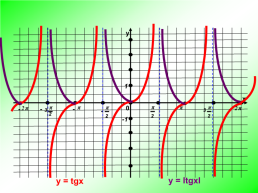
y = ItgxI
y = tgx

Функция y = ctg x
Область определения данной функции – все действительные числа, кроме чисел х=πk, k Z. Область значений функции – все действительные числа. Функция убывает на интервалах Функция нечетная, график ее симметричен относительно начала координат. Функция периодическая, ее наименьший положительный период равен π.
-

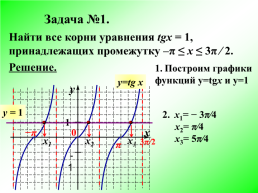
Задача №1.
Найти все корни уравнения tgx = 1, принадлежащих промежутку –π ≤ х ≤ 3π ∕ 2. Решение.
Построим графики функций у=tgx и у=1
х1= − 3π⁄4 х2= π⁄4 х3= 5π⁄4
−π
х1
х2
х3
3π/2
π

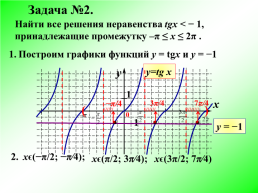
Задача №2.
Найти все решения неравенства tgx < − 1, принадлежащие промежутку –π ≤ х ≤ 2π .
Построим графики функций у = tgx и у = −1
−π/4
3π/4
7π/4
(
)
//////
//////
////////
хϵ(−π/2; −π⁄4);
хϵ(π/2; 3π⁄4);
хϵ(3π/2; 7π⁄4)