Презентация - Квадратный трехчлен

Квадратный трехчлен
Учитель математики ГБОУ СОШ №339 Павлова Л.В.

Введение
Тема «квадратный трехчлен» занимает в курсе алгебры одно из центральных мест.
В блоке «Алгебра» можно выделить 3 основных содержательно-методических линии: - тождественные преобразования - уравнения и неравенства - функции, их свойства и графики
Из «Примерной программы основного общего образования по математике» видно, что тема «Квадратный трехчлен» нашла свое отражение во всех трех аспектах.

Введение
Задания, где применяется данная тема включены в материалы ОГЭ (№15 в 1 части, №21 и №24 во второй части) Также данная тема может быть применена и при решении заданий из ЕГЭ (№13 и №15 во второй части ЕГЭ «Профильного») В учебнике алгебры под реакцией Ю. Н. Макарычев тема «Квадратный трехчлен» рассматривается подробно в 9-м классе. В учебнике под редакцией Ю. М. Колягина ей выделено меньше времени и в 8-м классе (при изучении темы «Теорема Виета») Однако, следует отметить, что учащиеся знакомятся с квадратным трехчленом еще в 7 классе при изучении тем «Многочлены» и «Разложение многочленов на множители».

Введение
В учебнике под редакцией Ю. М. Колягина в 7 классе учащиеся уже знакомятся с один из способов разложения квадратного трехчлена на множители (через формулы сокращенного умножения и вынесение общего множителя за скобки)
Например
Важно, что и в старшей школе (10-11 классы) данная тема находит свое применение при решении показательных, логарифмических, тригонометрических уравнений и неравенств.

Цели и результаты
Цели: Исходя из вышеизложенного я бы выделила следующие цели обучения данной теме: Развитие аналитико-логического мышления Установление взаимосвязи между квадратным трехчленом и квадратичной функцией. Развитие умения рационально подходить к решению поставленной задачи. Упрощение восприятия и усвоения материала в старшей школы. Успешная подготовка к сдаче ОГЭ и ЕГЭ

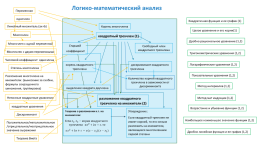
Логико-математический анализ
Переменная
одночлен
Квадратичная функция и ее график (1)
Линейный множитель (ax+b)
Корень многочлена
Целое уравнение и его корни(1)
Многочлен
квадратный трехчлен (1)
Дробно рациональное уравнение (1,2)
Многочлен с одной переменной
Старший коэффициент
Свободный член квадратного трехчлена
Многочлен с двумя переменными
Тригонометрические уравнения (1,2)
Числовой коэффициент одночлена
Логарифмические уравнения (1,2)
корень квадратного трехчлена
дискриминант квадратного трехчлена
Степень многочлена
Показательные уравнения (1,2)
Разложение многочлена на множители: (вынесение за скобки, формулы сокращенного умножения, группировка)
Количество корней квадратного трехчлена в зависимости от дискриминанта
Метод интервалов (1,2)
выделение квадрата двучлена
Неполные квадратные уравнения
Метод мат индукции (1,2)
разложение квадратного трехчлена на множители (2)
квадратные уравнения
Возрастание и убывание функции (1,2)
Утверждение: Если квадратный трехчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени
Дискриминант
Наибольшее наименьшее значение функции (1,2)
Положительное/неположительное/отрицательное/неотрицательное значение выражения
Дробно линейная функция и ее график (1,2)
Теорема Виета

Основные типы задач
Нахождение значений выражений Разложение выражения на множители Сокращение дробей Решение квадратных уравнений Решение квадратных неравенств Нахождение наибольшего/наименьшего значения выражения/функции

Поурочное планирование темы (по учебнику под редакцией Ю. Н. Макарычева)
№ урока.Тема урока.Тип урока.Цели урока.Планируемые результаты.ДЗ
1.Квадратный трехчлен и его корни.Изучение нового материала.Ввести определение квадратного трехчлена, его корней; установить зависимость количества корней квадратного трехчлена от дискриминанта; научить выделять квадрат двучлена из квадратного трехчлена..Урок 1-4 Предметные: знать понятие квадратного трехчлена формулу разложения квадратного трехчлена на множители; уметь выделять квадрат двучлена из квадратного трехчлена; раскладывать квадратный трехчлен на множители различными способами. Личностные: уметь использовать навыки самоанализа, самопроверки, уметь находить и исправлять свои ошибки. Коммуникативные: вступать в диалог с учителем, участвовать в общей беседе. Познавательные: осознавать вопрос задачи; уметь находить рациональный способ решения задачи, уметь извлекать необходимую информацию при чтении материала учебника и прослушивании изложения материала учителем..№59 (б,г,е); № 60 (б,г,); №61 (б,г,); №62(б,г,); №65(б, г,)
2.Разложение квадратного трехчлена на множители.Комбинированный урок (продолжается изучение темы с созданием проблемной ситуации).Продолжить применение ранее изученного материала при решении задач. Вывести формулу разложения квадратного трехчлена на множители; научить применять эту формулу на практике.№77 (б, г); №78 (б, г); №84 (б) №85 (б)
3.Разложение квадратного трехчлена на множители.Урок закрепление полученных знаний и умений. Промежуточный контроль за состоянием знаний, умений и навыков учащихся.Продолжить изучение темы; выполнить промежуточный контроль за состоянием знаний, умений, навыков учащихся с целью выявления «пробелов»; закрепить применение теоретического материала при решении задач. Продолжить развитие алгоритмического и логического мышления у учащихся.№86 №87, №88, №89
4.Подготовка к контрольной работе по теме «Функции их свойства. Квадратный трехчлен, его корни разложение квадратного трехчлена на множители»..Урок – обобщения и систематизации (повторение и закрепление).Закрепление полученных знаний учащимися. Развитие аналитико-логического мышления; развитие алгоритмического мышления; развитие рационального подхода к решению задач. Формирование навыка самоанализа..Подготови- тельный Вариант кр
5.Контрольная работа по теме: «Функции их свойства. Квадратный трехчлен, его корни разложение квадратного трехчлена на множители»..Урок контроля знаний.Выявление знаний и умений учащихся. Формирование навыков самоанализа и самоконтроля. Формирование навыка регулировать собственную деятельность посредством письменной речи. Формирование навыка выбора наиболее эффективного способа решения задачи Научить организовывать выделенное на решение задачи время.Предметные: знать и уметь применять полученные знания на практике. Личностные: использование навыков самоанализа и самоконтроля Коммуникативные: уметь регулировать собственную деятельность посредством письменной речи Регулятивные: уметь оценивать достигнутый результат Познавательные: уметь выбирать рациональные и эффективные способы решения поставленной задачи.

Урок №1 Квадратный трехчлен и его корни
1) Организационный этап. Облако слов, составленное из слов – понятий, которые учащиеся уже знают и нового понятия, выделенного одним цветом. Задача учащихся - определить тему урока.
2) Постановка цели и задач урока.
Цели: Ввести определение квадратного трехчлена, его корней; установить зависимость количества корней квадратного трехчлена от дискриминанта; научить выделять квадрат двучлена из квадратного трехчлена. Задачи: научить использовать навыки самоанализа, самопроверки, научить находить и исправлять свои ошибки, научить извлекать необходимую информацию, научить вступать в диалог и аргументировать свое мнение

3) Актуализация знаний. 1. Повторение темы многочлен Вопросы: Что такое одночлен? Что такое многочлен? Что такое степень одночлена?
Одночлены:.Многочлены:
.
.
.
.
2. Вспомнить как решаются квадратные уравнения.
№74 (неч) Решить уравнение: (Решает 1 учащийся на доске, учитель помогает вопросами, остальные ученики решают в тетради)

Первичное усвоение новых знаний. 1. Давайте сформулируем понятие квадратного трехчлена. Как вы думаете, если речь идет о трехчлене, сколько должно быть слагаемых в многочлене? Что означает понятие «Квадратный»? 2. Попробуйте сформулировать определение квадратного трехчлена (возможные варианты: трехчлен, где все одночлены 2 степени, трехчлен, где есть одночлен 2 степени) 3. Дать определение квадратного трехчлена:
Определение. Квадратным трехчленом называется многочлен вида ax2+bx+c, где x – переменная, a, b, c – некоторые числа, причем a≠0
6) Усвоение новых знаний. Ввести понятие корней квадратного трехчлена. Задать устные вопросы: Что такое уравнение? Что называется корнями уравнения? Рассмотрим пример 1 (п3 пар2, стр 20): Найти корни квадратного трехчлена 3x2-2x-5
Корнями квадратного трехчлена ax2+bx+c называются корни уравнения ax2+bx+c=0

7) Первичное закрепление.
3) Решить № 59 (а, в, д) №60 (а, в) (№59 а – решает учитель, остальное учащиеся под руководством учителя) 4)Выяснить количество корней квадратного трехчлена в зависимости от дискриминанта квадратного трехчлена на примере решение №61(а, в) №62 (а, в) 5)Выделение квадрата двучлена из квадратного трехчлена Рассмотреть пример 2 (п3 пар2, стр 21)
Решить № 64, 65 (a, в)

9) Рефлексия (подведение итогов занятия) Подведение итогов занятия, выставление оценок, объявление галочек за урок (система 5 галочек оценка 5), вопросы по уроку. На специальной доске ставят галочки в одну из ячейки таблицы.
Понял урок, было интерсно.Не понял урок, но было интересно
Понял урок, было не интересно.Не понял урок, было не интересно

Урок №2 Разложение квадратного трехчлена на множители

Решить вышеприведенный пример эти способом и сравнить время, затраченное на решение, установив таким образом полезность данный формулы.

III. Закрепление изученного материала Использование выведенной формулы на практике Пример №1,2 (стр 25) +№77 (а, в,); №78 (а, в) Вопрос: Где может быть использована данная формула? (Ответ: при сокращении дробей) Пример №3 (стр26) + №84 (а); №85(а) IV. Домашнее задание №77 (б, г); №78 (б, г); №84 (б) №85 (б)

Урок №3 Разложение квадратного трехчлена на множители
Ход урока Проверка усвоения знаний. Проверочная работа:
Кол-во баллов.Оценка
0-2.2
3.3
4.4
5.5
№ задания.Балл
1.1
2.1
3.1
4.2

II. Провести анализ проверочной работы, наиболее сложные задания разобрать на доске. III. Продолжение изучения темы (связь квадратного трехчлена и функции)
Построить графики функции:
Вопрос: В чем различие графиков этих функций? (Ответ: различна О.О.Ф., на втором графике выколота 1 точка)

Урок №4 Подготовка к контрольной работе по теме «Функции их свойства. Квадратный трехчлен, его корни разложение квадратного трехчлена на множители».
Ход урока: Проверка Д/З . Анализ ошибок допущенных при выполнении д/з и проверочной работы
2) Область определения функции y= ϕ(x) отрезок [-6;5]. Найдите нули функции, промежутки возрастания/убывания, наибольшее/наименьшее значение функции.

Вынести за скобки общий множитель Формулы сокращенного умножения Способ группировки Разложение квадратного трехчлена н множители
Домашнее задание: Подготовиться к контрольной работе (учитель выдаст подготовительный вариант КР)

Урок №5 Контрольная работа по теме «Функции их свойства. Квадратный трехчлен, его корни разложение квадратного трехчлена на множители».
Контрольная работа
Задание.балл
1а.1
1b.1
2a.1
2b.1
3a.1
3b.1
3c.1
4.2
5.2
балл.оценка
0-5.«2»
6-7.«3»
8-9.«4»
10-11.«5»

Частные случаи нахождения корней квадратного трехчлена

Частные случаи нахождения корней квадратного трехчлена

Частные случаи нахождения корней квадратного трехчлена

Использование темы «Квадратный трехчлен, его корни, разложение на множители»
ОГЭ №15 (I часть) При решении квадратных неравенств №21 (II часть) При решении квадратных уравнений №23 (II часть) При построении графиков ЕГЭ «Базовый» №7 При решении квадратных уравнений №17 при решении квадратных неравеств
ЕГЭ «Профильный» №5 (I часть) Простейшие уравнения №13 (С-1, II часть) Уравнения №15 (С-3, II часть). Решение неравенств
Далее на слайдах *все задания взяты с сайта Д. Д. Гущина «Решу ОГЭ» **все задания взяты с сайта Д. Д. Гущина «Решу ЕГЭ «математика базового уровня»» ***все задания взяты с сайта Д. Д. Гущина «Решу ЕГЭ «математика профильного уровня»»

Использование темы «Квадратный трехчлен, его корни, разложение на множители» в заданиях ОГЭ
№15 (I часть) При решении квадратных неравенств
(314579)*

Использование темы «Квадратный трехчлен, его корни, разложение на множители» в заданиях ЕГЭ «базовый»
№7 при решении квадратных уравнений
(506842)**
(100879)**
x2+11x=-28 x2+11x+28=0 x1=-7 ;x2=-4 Ответ -7
Ответ: -3
№17 при решении квадратных неравенств
(511990)**
(512614)**

Использование темы «Квадратный трехчлен, его корни, разложение на множители» в заданиях ЕГЭ «профильный»
№13 (С-1, II часть) Уравнения (№514623)***
№13 (С-1, II часть) Уравнения (№516779)***

Использование темы «Квадратный трехчлен, его корни, разложение на множители» в заданиях ЕГЭ «профильный»
№15 (С-3, II часть) Решение неравенств
По схеме Горнера
.12.-16.3.1
X=1.12.-4.-1.0
Таким образом отмечаем точки: x=-16;x=12зн!ч;x=1;x=2 (зн!)

Формулировка понятия «квадратный трехчлен»
2 этап: Ввести термин «квадратный трехчлен» Попросить учащихся самостоятельно сформулировать определение задавая наводящие вопросы. Как вы думаете, если речь идет о трехчлене, сколько должно быть слагаемых в многочлене? Что означает понятие «Квадратный»? Обращая внимание на «необходимое» для данного понятия сформулировать определение:
Квадратным трехчленом называется многочлен вида ax2+bx+c, где x – переменная, a, b, c – некоторые числа, причем a≠0

Формулировка понятия «квадратный трехчлен»

Формулировка понятия «корень квадратного трехчлена»
1 этап: Систематизировать другие понятия, входящие в данное понятие Уравнение с одной переменной, корни уравнения Задать устные вопросы: Что такое уравнение? Что называется корнями уравнения? 2 этап: Ввести понятие «корни квадратного трехчлена» Корнями квадратного трехчлена ax2+bx+c называются корни уравнения ax2+bx+c=0 3 этап: Закрепление усвоения понятия в процессе решения практических задач №59(а,в,д); №60(а,в); №61(а,в); №62(а,в) (задания решают учащиеся на доске, учитель контролирует процесс и помогает в случае необходимости) 4 этап: контроль за усвоением данного понятия. Контроль будет проведен на последующих уроках во время проведения проверочной работы (3 урок по теме) и контрольной работы (5 урок по теме)

Этапы работы с теоремой о разложении квадратного трехчлена на множители:
Подчеркнуть, что применение этой формулы упрощает решение задачи.

Учебно-методический комплекс
Учебник Ю. Н. Макарычев «Алгебра 9 класс» Презентации к урокам №1, №2, №3, №4, №5 (пример: презентация к уроку №1) Поурочные планы по учебнику Ю.Н. Макарычева «алгебра 9 класс» Рабочая тетрадь по алгебре Т. М. Ерина, М. Ю. Ерина. (к учебнику Ю.Н. Макарычева)

Список литературы
Учебник Ю. Н. Макарычев «Алгебра» 7 класс Учебник Ю. Н. Макарычев «Алгебра» 8 класс Учебник Ю. Н. Макарычев «Алгебра» 9 класс Учебник Ш. А. Алимов «Алгебра» 8 класс Учебник Ш. А. Алимов «Алгебра» 9 класс Учебник Ш. А. Алимов «Алгебра и начала математического анализа» 10-11 класс