Презентация - Построение таблиц истинности для логических выражений

Задание 2 Построение таблиц истинности для логических выражений
Автор: Никитенко Евгений Игоревич учитель информатики МБОУ СОШ №10 п.Гирей
ЕГЭ по информатике

Выберите номер задания
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Задание 7
Задание 8
Задание 9
Задание 10

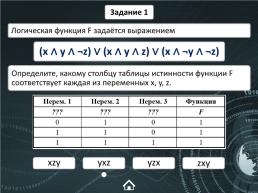
Задание 1
Логическая функция F задаётся выражением
(x ∧ y ∧ ¬z) ∨ (x ∧ y ∧ z) ∨ (x ∧ ¬y ∧ ¬z)
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
xzy
yzx
zxy
yxz

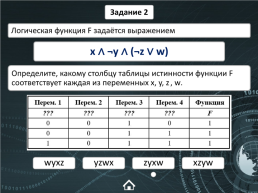
Задание 2
Логическая функция F задаётся выражением
x ∧ ¬y ∧ (¬z ∨ w)
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
wyxz
yzwx
xzyw
zyxw

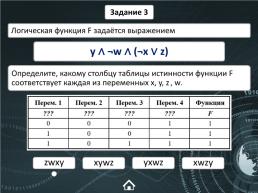
Задание 3
Логическая функция F задаётся выражением
y ∧ ¬w ∧ (¬x ∨ z)
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
zwxy
yxwz
xywz
xwzy

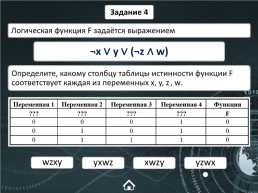
Задание 4
Логическая функция F задаётся выражением
¬x ∨ y ∨ (¬z ∧ w)
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
wzxy
yxwz
xwzy
yzwx

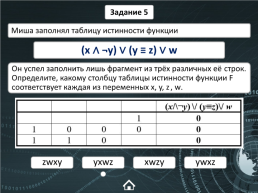
Задание 5
Миша заполнял таблицу истинности функции
(x ∧ ¬y) ∨ (y ≡ z) ∨ w
Он успел заполнить лишь фрагмент из трёх различных её строк. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
ywxz
zwxy
yxwz
xwzy

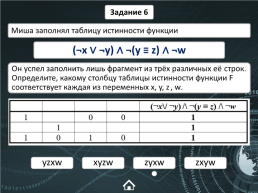
Задание 6
Миша заполнял таблицу истинности функции
(¬x ∨ ¬y) ∧ ¬(y ≡ z) ∧ ¬w
Он успел заполнить лишь фрагмент из трёх различных её строк. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
yzxw
zxyw
zyxw
xyzw

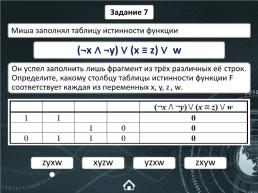
Задание 7
Миша заполнял таблицу истинности функции
(¬x ∧ ¬y) ∨ (x ≡ z) ∨ w
Он успел заполнить лишь фрагмент из трёх различных её строк. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
yzxw
zxyw
zyxw
xyzw

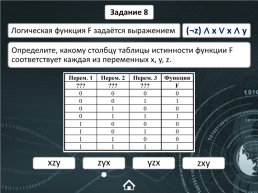
Задание 8
Логическая функция F задаётся выражением
(¬z) ∧ x ∨ x ∧ y
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
xzy
yzx
zxy
zyx

Задание 9
Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы. Каким из приведённых ниже выражений может быть F?

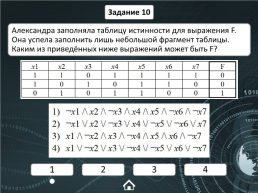
Задание 10
Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы. Каким из приведённых ниже выражений может быть F?

Источники:
1. ФИПИ: Открытый банк заданий ЕГЭ по информатике 2. Демонстрационные варианты ЕГЭ по информатике прошлых лет
Изображения:
Фон 1 слайда Кнопка «Домой» Кнопка «Выход» Скриншоты заданий с открытого банка заданий ЕГЭ по информатике