Презентация - Линейная функция и её график
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 82%
- Слайдов: 27
- Просмотров: 2229
- Скачиваний: 705
- Размер: 0.42 MB
- Класс: 7
- Формат: ppt / pptx
Примеры похожих презентаций
 Линейная функция и её график
Линейная функция и её график Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций … По улицам Архангельска. Линейная функция, её график и свойства
… По улицам Архангельска. Линейная функция, её график и свойства Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций Построение и исследование графиков функций с использованием программного обеспечения компьютеров
Построение и исследование графиков функций с использованием программного обеспечения компьютеров Понятие функции и ее график
Понятие функции и ее график
Слайды и текст этой онлайн презентации
Слайд 1

Линейная функция
и её график
Слайд 2

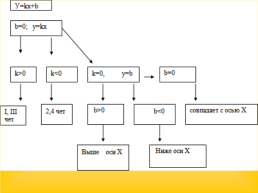
На прошлом уроке мы узнали: *Функция вида у = kx + b называется линейной. *Графиком функции вида у = kx + b является прямая. *Для построения прямой необходимы только две точки, так как через две точки проходит единственная прямая. *Коэффициент k показывает возрастает или убывает прямая. *Коэффициент b показывает, в какой точке прямая пересекает ось OY. *Условие параллельности двух прямых.
Слайд 3
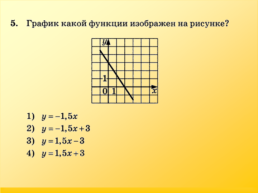
Слайд 4
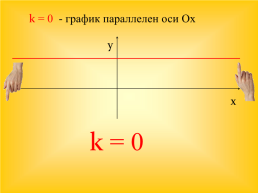
k = 0 - график параллелен оси Ох
y
x
k = 0
y
x
k = 0
Слайд 5
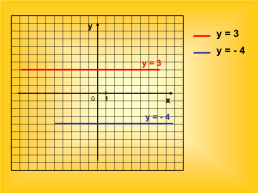
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
у
у = 3
у = - 4
у = 3
х
у = - 4
Слайд 6
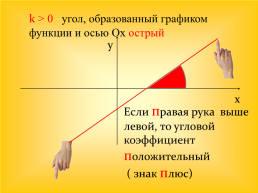
k > 0 угол, образованный графиком функции и осью Ох острый
y
х
Если правая рука выше левой, то угловой коэффициент положительный ( знак плюс)
y
х
Если правая рука выше левой, то угловой коэффициент положительный ( знак плюс)
Слайд 7
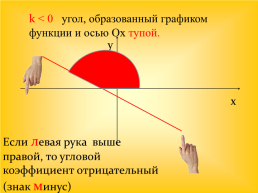
k < 0 угол, образованный графиком функции и осью Ох тупой.
y
x
Если левая рука выше правой, то угловой коэффициент отрицательный (знак минус)
y
x
Если левая рука выше правой, то угловой коэффициент отрицательный (знак минус)
Слайд 8
Слайд 9
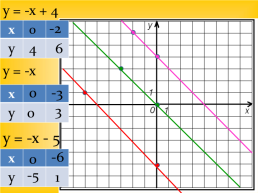
у = -х + 4
-2
х..
у..
у = -х
-3
х..
у..
у = -х - 5
-6
х..
у..
-5
-2
х..
у..
у = -х
-3
х..
у..
у = -х - 5
-6
х..
у..
-5
Слайд 10

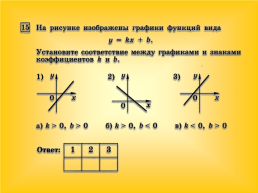
Графики, каких из заданных функций параллельны графику функции у = 2х +1
у = 2х , у = х +1, у = 2х -1, у = - 2х +1, у = -2х
у = 2х,
у = 2х -1.
у = - 2х +1, у = -2х.
у = 2х,
у = 2х -1.
у = - 2х +1, у = -2х.
Слайд 11

Выяснить взаимное расположение графиков функций:
у = 7х – 4 и у = 7х + 5
у = 10х – 3 и у = -10х+6
у = 0,3 + 2 и у = 8,1х + 3
у = -7х + 3 и у = -7х +2
у = 3х + 2, у = 2,3х + 2 и у = - 2,3 х + 2
Слайд 12

Найдите координату точки пересечения графиков функций
у = -2х +7 и у =0,5х – 5,5
Решим уравнение.
-2х + 7 = 0,5х – 5,5,
-2х – 0,5х = - 5,5 – 7,
-2,5х = -12,5,
х = - 12,5 : ( -2,5)
х = 5.
у = -2 • 5 + 7,
у = - 3
Координата точки пересечения прямых ( 5; -3)
Решим уравнение.
-2х + 7 = 0,5х – 5,5,
-2х – 0,5х = - 5,5 – 7,
-2,5х = -12,5,
х = - 12,5 : ( -2,5)
х = 5.
у = -2 • 5 + 7,
у = - 3
Координата точки пересечения прямых ( 5; -3)
Слайд 13

Не выполняя построения графика функции у = 2х +3, выяснить проходит ли он через точку А (-3;-3) ?
Решение.
Т.к. точка А имеет координату (-3; -3), то х = - 3, у = - 3 получим:
- 3 = 2 • ( - 3) + 3 – верно, значит
график функции проходит через точку А
Решение.
Т.к. точка А имеет координату (-3; -3), то х = - 3, у = - 3 получим:
- 3 = 2 • ( - 3) + 3 – верно, значит
график функции проходит через точку А
Слайд 14

Не выполняя построения, найдите координаты точек пересечения графика функции у = - 2х – 6 с осями координат.
Решение.
С осью х, у = 0, - 2 х – 6 = 0,
- 2 х = 6,
х = -3.
Координата точки пересечения с осью х (- 3,0).
С осью у, х = 0,
у = - 2 • 0 – 6 = - 6
Координата точки пересечения с осью у (0,- 6).
Решение.
С осью х, у = 0, - 2 х – 6 = 0,
- 2 х = 6,
х = -3.
Координата точки пересечения с осью х (- 3,0).
С осью у, х = 0,
у = - 2 • 0 – 6 = - 6
Координата точки пересечения с осью у (0,- 6).
Слайд 15

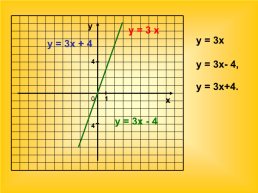
В одной координатной плоскости постройте графики функций:
у = 3х, у = 3х- 4, у = 3х+4.
Слайд 16
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
у
у = 3 х
у = 3х у = 3х- 4, у = 3х+4.
у = 3х + 4
х
у = 3х - 4
Слайд 17
Слайд 18
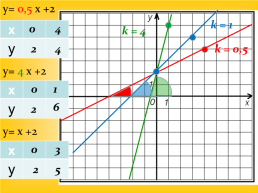
y= 0,5 х +2
k = 1
х..
у..
k = 4
k = 0,5
y= 4 х +2
х..
у..
y= х +2
х..
у..
k = 1
х..
у..
k = 4
k = 0,5
y= 4 х +2
х..
у..
y= х +2
х..
у..
Слайд 19
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
...................
у
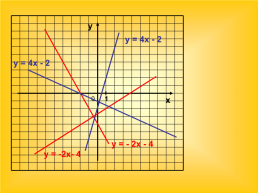
у = 4х - 2
у = 4х - 2
х
у = - 2х - 4
у = -2х- 4
Слайд 20
...................
...................
...................
...................
...................
...................
...................
...................
.........1..........
...................
.........0..........
...................
...................
...................
...................
...................
...................
...................
...................
...................
у
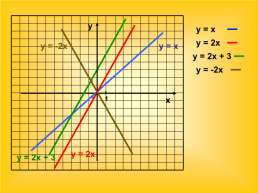
у = х
у = 2х
у = -2х
у = х
у = 2х + 3
у = -2х
х
у = 2х
у = 2х + 3
Слайд 21

1. График функции у = 7х проходит через точку, абсцисса которой равна 4. Чему равна ордината этой точки?
Л – 28;
А – 7; Е – 12; К – 4
2. График функции у = -2х проходит через точку, ордината которой равна 10. Чему равна абсцисса этой точки?
М – 4;
Е – (- 5);
А – 5; Р (-10)
3. Какая из точек принадлежит графику функции у = 4х
Й (3; 12):
А (-2; 2),
С (10; 25); О (1,6).
4. График функции у = kх проходит через точку А (6;-18). Чему равно k?
Б – (- 3 ),
А – 4, М – 3 , С – 3.
Л – 28;
А – 7; Е – 12; К – 4
2. График функции у = -2х проходит через точку, ордината которой равна 10. Чему равна абсцисса этой точки?
М – 4;
Е – (- 5);
А – 5; Р (-10)
3. Какая из точек принадлежит графику функции у = 4х
Й (3; 12):
А (-2; 2),
С (10; 25); О (1,6).
4. График функции у = kх проходит через точку А (6;-18). Чему равно k?
Б – (- 3 ),
А – 4, М – 3 , С – 3.
Слайд 22

5. В каких четвертях расположен график функции у = kх, если k – положительно?
Ш – в первой и второй, А - во второй и третьей,
Р - во второй и четвертой,
Н - в первой и третьей.
6. В каких четвертях расположен график функции у = kх, если k –отрицательно? П – в первой и второй, Ж - в первой и третьей, Д - во второй и третьей,
И - во второй и четвертой.
7. Проходит ли график функции у = 2х, через точку с координатой (2;4)? Р- нет, А – не знаю, М – другой ответ,
Ц - да.
Л е й б
н
и
ц
Н - в первой и третьей.
6. В каких четвертях расположен график функции у = kх, если k –отрицательно? П – в первой и второй, Ж - в первой и третьей, Д - во второй и третьей,
И - во второй и четвертой.
7. Проходит ли график функции у = 2х, через точку с координатой (2;4)? Р- нет, А – не знаю, М – другой ответ,
Ц - да.
Л е й б
н
и
ц
Слайд 23

Готфрид Вильгельм Лейбниц
Ввел многие понятия и символы, употребляемые в математике и сейчас, в частности, им введен термин «функция»
Слайд 24

Постройте графики функций , содержащий модуль:
у = |х|, у = |х| + 2, у = |х - 3|,
используя определение модуля.
Слайд 25
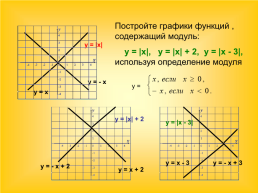
Постройте графики функций , содержащий модуль:
у = |х|, у = |х| + 2, у = |х - 3|, используя определение модуля
у = |х|
у = - х
у = х
у = |х| + 2
у = |х - 3|
у = х - 3
у = - х + 3
у = - х + 2
у = х + 2
у = |х|
у = - х
у = х
у = |х| + 2
у = |х - 3|
у = х - 3
у = - х + 3
у = - х + 2
у = х + 2
Слайд 26

Из данных функций выберите те, которые являются линейными?
у= 4 х + 2,
у = 1,5 х,
у = х + 2,5,
у = 4 х² - 5 х – 1,
у = -8 ,
у = х² + 2,5,
у =
у= 5 х – 2,
у = -2 х,
Слайд 27

Список использованной литературы
1.Учебник "Алгебра " для 7 класса.
Авторы: Алимов А.Ш, Колягин Ю.М. и др.
Год издания: 2007 М.:
Издательство Просвещение,
2. Дидактические материалы по алгебре для 7 класса.
Авторы: Ю.Н.Макарычев, Н.Г.Миндюк, Л.М.Короткова
Год издания: 2007 М.
Издательство Просвещение
3.Изучение алгебры
Книга для учителя
Авторы: Ю.М.Колягин, Ю.В. Сидоров и др..
Год выпуска: 2002
Издательство: М, Просвещение
4.http://www.syrtsovasv.narod.ru
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
