Презентация - Построение сечений тетраэдра и параллелепипеда
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 93%
- Слайдов: 41
- Просмотров: 1512
- Скачиваний: 63
- Размер: 0.57 MB
- Онлайн: Да
- Формат: ppt / pptx
Слайды и текст этой онлайн презентации
Слайд 1

ПОСТРОЕНИЕ СЕЧЕНИЙ
тетраэдра и параллелепипеда
Цель урока: научиться строить сечения тетраэдра и параллелепипеда плоскостью. формировать умения анализировать, сравнивать, обобщать, делать выводы; развивать навыки самостоятельной деятельности у обучающихся, умения работать в группе.
Цель урока: научиться строить сечения тетраэдра и параллелепипеда плоскостью. формировать умения анализировать, сравнивать, обобщать, делать выводы; развивать навыки самостоятельной деятельности у обучающихся, умения работать в группе.
Слайд 2

ЦЕЛИ УРОКА:
Образовательные: Проверить знание теоретического материала о многогранниках (тетраэдр, параллелепипед). Продолжить формирование умения анализировать чертеж, выделять главные элементы при работе с моделью многогранника, намечать ход решения задачи, предвидеть конечный результат. Отработать навыки решения задач на построение сечений многогранников. Развивать графическую культуру и математическую речь. Формировать навыки использования компьютерных технологий на уроках геометрии. Развивающие: Развивать познавательный интерес учащихся. Формировать и развивать у учащихся пространственное воображение. Воспитательные: Воспитывать самостоятельность, аккуратность, трудолюбие. Воспитывать умения работать индивидуально над задачей. Воспитывать волю и настойчивость для достижения конечных результатов.
Образовательные: Проверить знание теоретического материала о многогранниках (тетраэдр, параллелепипед). Продолжить формирование умения анализировать чертеж, выделять главные элементы при работе с моделью многогранника, намечать ход решения задачи, предвидеть конечный результат. Отработать навыки решения задач на построение сечений многогранников. Развивать графическую культуру и математическую речь. Формировать навыки использования компьютерных технологий на уроках геометрии. Развивающие: Развивать познавательный интерес учащихся. Формировать и развивать у учащихся пространственное воображение. Воспитательные: Воспитывать самостоятельность, аккуратность, трудолюбие. Воспитывать умения работать индивидуально над задачей. Воспитывать волю и настойчивость для достижения конечных результатов.
Слайд 3

ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ
Задачи на построение сечений в многогранниках занимают заметное место в курсе стереометрии. Их роль обусловлена тем, что решение этого вида задач способствует усвоению аксиом стереометрии, следствий из них, развитию пространственных представлений и конструктивных навыков. Умение решать задачи на построение сечений является основой изучения почти всех тем курса стереометрии. При решении многих стереометрических задач используют сечения многогранников плоскостью. На предыдущих уроках мы с вами познакомились с аксиомами стереометрии, следствиями из аксиом и с теоремами о параллельности прямых и плоскостей в пространстве. Мы рассмотрели алгоритмы построения несложных сечений куба, тетраэдра и параллелепипеда. Эти сечения, как правило, задавались точками, расположенными на ребрах или гранях многогранника. Сегодня на уроке мы с вами повторим геометрические утверждения, позволяющие сформулировать правила построения сечений. А также научимся применять эти знания при решении задачи на построение сечения тетраэдра и параллелепипеда плоскостью, проходящей через три данные точки, такие, что никакие три из этих точек не лежат в одной грани
Задачи на построение сечений в многогранниках занимают заметное место в курсе стереометрии. Их роль обусловлена тем, что решение этого вида задач способствует усвоению аксиом стереометрии, следствий из них, развитию пространственных представлений и конструктивных навыков. Умение решать задачи на построение сечений является основой изучения почти всех тем курса стереометрии. При решении многих стереометрических задач используют сечения многогранников плоскостью. На предыдущих уроках мы с вами познакомились с аксиомами стереометрии, следствиями из аксиом и с теоремами о параллельности прямых и плоскостей в пространстве. Мы рассмотрели алгоритмы построения несложных сечений куба, тетраэдра и параллелепипеда. Эти сечения, как правило, задавались точками, расположенными на ребрах или гранях многогранника. Сегодня на уроке мы с вами повторим геометрические утверждения, позволяющие сформулировать правила построения сечений. А также научимся применять эти знания при решении задачи на построение сечения тетраэдра и параллелепипеда плоскостью, проходящей через три данные точки, такие, что никакие три из этих точек не лежат в одной грани
Слайд 4

Актуализация знаний
Чтобы перейти к закреплению темы, давайте повторим теоретический материал, ответив на вопросы: Что называется секущей плоскостью (слайд 6)? (Обучающиеся дают определение.) Что называется сечением многогранника (слайд 7)? (Формулируется определение.) Что необходимо сделать для того, чтобы построить сечение многогранника плоскостью? Построение сечения сводится к построению линий пересечения секущей плоскости и плоскостей граней многогранника.)
Чтобы перейти к закреплению темы, давайте повторим теоретический материал, ответив на вопросы: Что называется секущей плоскостью (слайд 6)? (Обучающиеся дают определение.) Что называется сечением многогранника (слайд 7)? (Формулируется определение.) Что необходимо сделать для того, чтобы построить сечение многогранника плоскостью? Построение сечения сводится к построению линий пересечения секущей плоскости и плоскостей граней многогранника.)
Слайд 5

ПРАВИЛА ПОСТРОЕНИЯ СЕЧЕНИЙ
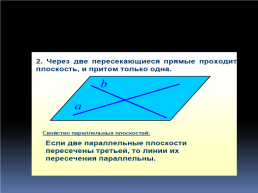
Давайте повторим правила, о которых необходимо помнить при построении сечений многогранника (обучающиеся вспоминают и формулируют нужные аксиомы, теоремы, свойства): Если две точки принадлежат секущей плоскости и плоскости некоторой грани многогранника, то прямая, проходящая через данные точки, будет являться следом секущей плоскости на плоскости грани. Если секущая плоскость параллельна прямой, лежащей в некоторой плоскости, и пересекает эту плоскость, то линия пересечения этих плоскостей параллельна данной прямой. При пересечении двух параллельных плоскостей секущей плоскостью получаются параллельные прямые. Если секущая плоскость параллельна некоторой плоскости, то эти две плоскости пересекают третью плоскость по прямым, параллельным между собой. Если у секущей плоскости и плоскостей двух пересекающихся граней есть общая точка, то она лежит на прямой, содержащей общее ребро данных граней
Давайте повторим правила, о которых необходимо помнить при построении сечений многогранника (обучающиеся вспоминают и формулируют нужные аксиомы, теоремы, свойства): Если две точки принадлежат секущей плоскости и плоскости некоторой грани многогранника, то прямая, проходящая через данные точки, будет являться следом секущей плоскости на плоскости грани. Если секущая плоскость параллельна прямой, лежащей в некоторой плоскости, и пересекает эту плоскость, то линия пересечения этих плоскостей параллельна данной прямой. При пересечении двух параллельных плоскостей секущей плоскостью получаются параллельные прямые. Если секущая плоскость параллельна некоторой плоскости, то эти две плоскости пересекают третью плоскость по прямым, параллельным между собой. Если у секущей плоскости и плоскостей двух пересекающихся граней есть общая точка, то она лежит на прямой, содержащей общее ребро данных граней
Слайд 6
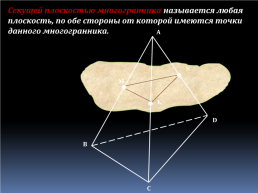
Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника.
Слайд 7

Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Слайд 8
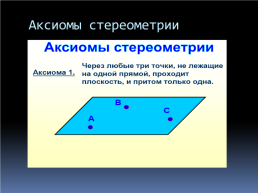
Аксиомы стереометрии
Слайд 9

Слайд 10
Слайд 11
Слайд 12
Слайд 13

Слайд 14

Слайд 15
Слайд 16
Слайд 17
Слайд 18
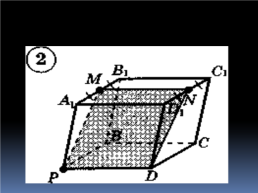
Слайд 19
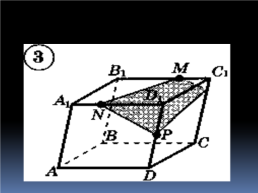
Слайд 20
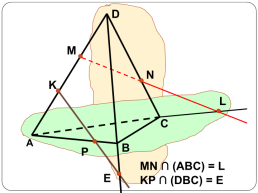
MN ∩ (ABC) = L
KP ∩ (DBC) = E
Слайд 21
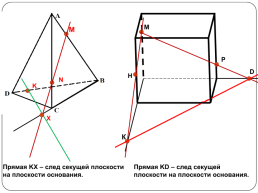
M
N
K
Прямая KX – след секущей плоскости на плоскости основания.
Прямая KD – след секущей плоскости на плоскости основания.
Слайд 22
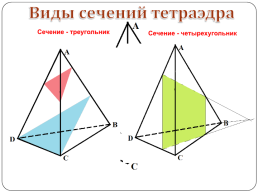
Виды сечений тетраэдра
Слайд 23
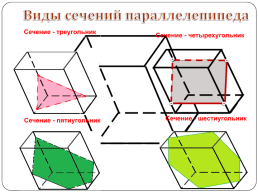
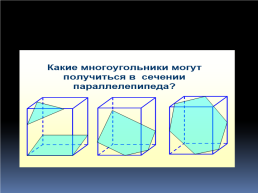
Виды сечений параллелепипеда
Слайд 24
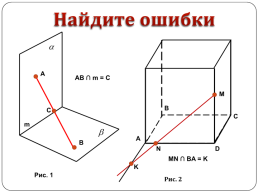
Найдите ошибки
A
AB ∩ m = C
M
B
C
C
m
A
B
N
D
MN ∩ BA = K
K
Рис. 1
Рис. 2
A
AB ∩ m = C
M
B
C
C
m
A
B
N
D
MN ∩ BA = K
K
Рис. 1
Рис. 2
Слайд 25
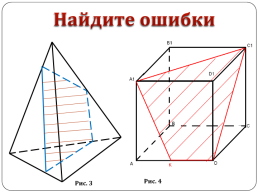
Найдите ошибки
Рис. 4
Рис. 3
Рис. 4
Рис. 3
Слайд 26
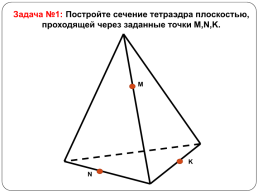
Задача №1: Постройте сечение тетраэдра плоскостью, проходящей через заданные точки M,N,K.
Слайд 27
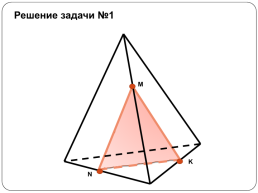
Решение задачи №1
Слайд 28
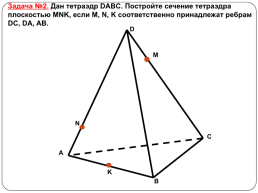
Задача №2. Дан тетраэдр DABC. Постройте сечение тетраэдра плоскостью MNK, если M, N, K соответственно принадлежат ребрам DC, DA, AB.
Слайд 29
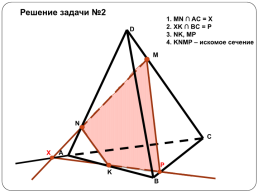
Решение задачи №2
1. MN ∩ AC = X 2. XK ∩ BC = P 3. NK, MP 4. KNMP – искомое сечение
1. MN ∩ AC = X 2. XK ∩ BC = P 3. NK, MP 4. KNMP – искомое сечение
Слайд 30
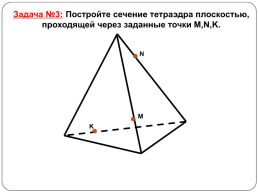
Задача №3: Постройте сечение тетраэдра плоскостью, проходящей через заданные точки M,N,K.
Слайд 31
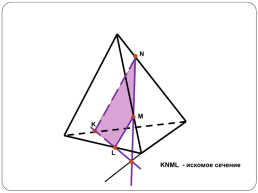
KNML - искомое сечение
Слайд 32
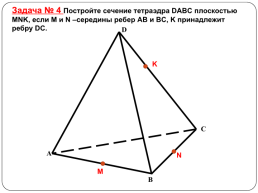
Задача № 4 Постройте сечение тетраэдра DABC плоскостью MNK, если M и N –середины ребер AB и BC, K принадлежит ребру DC.
Слайд 33
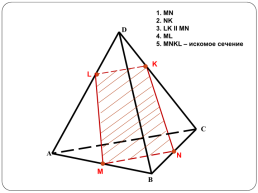
1. MN
2. NK
3. LK II MN
4. ML
5. MNKL – искомое сечение
L
L
Слайд 34
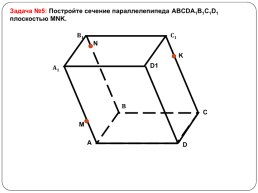
Задача №5: Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью MNK.
Слайд 35
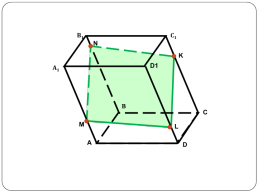
Слайд 36
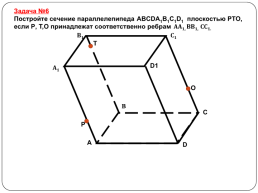
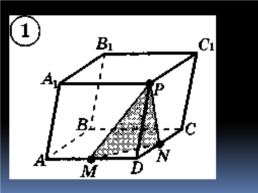
Задача №6 Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью PTO, если P, T,O принадлежат соответственно ребрам АА1, ВВ1, СС1.
Слайд 37
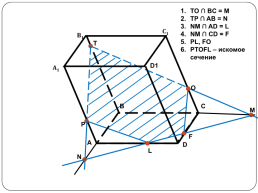
TO ∩ BC = M
TP ∩ AB = N
NM ∩ AD = L
NM ∩ CD = F
PL, FO
PTOFL – искомое сечение
Слайд 38
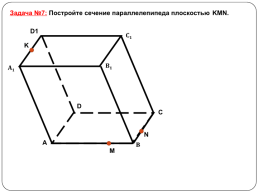
Задача №7: Постройте сечение параллелепипеда плоскостью KMN.
Слайд 39
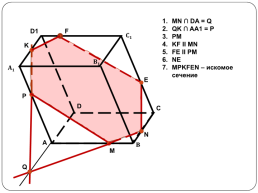
MN ∩ DA = Q
QK ∩ AA1 = P
PM
KF II MN
FE II PM
NE
MPKFEN – искомое сечение
Слайд 40

Итог урока:
«Мне понравился (не понравился) урок, потому что…» «Сегодня на уроке я научился….» «Мне хочется, чтобы….» «В этот урок я добавил(а) бы …»
«Мне понравился (не понравился) урок, потому что…» «Сегодня на уроке я научился….» «Мне хочется, чтобы….» «В этот урок я добавил(а) бы …»
Слайд 41

Спасибо за урок!!!
Задание на дом: п.14 №105, 106. (Дополнительное задание к № 105 на карточке)
Задание на дом: п.14 №105, 106. (Дополнительное задание к № 105 на карточке)
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.







