Презентация - Параллелепипед - Задачи на построение сечений
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 96%
- Слайдов: 42
- Просмотров: 5094
- Скачиваний: 2155
- Размер: 3.75 MB
- Онлайн: Да
- Формат: ppt / pptx
Примеры похожих презентаций
 Задачи на построение сечений
Задачи на построение сечений Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Построение сечений параллелепипеда 10 класс
Построение сечений параллелепипеда 10 класс Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Тетраэдр - Задачи на построение сечений
Тетраэдр - Задачи на построение сечений Задачи на построение сечений
Задачи на построение сечений Решение задач на построение изображений в линзах
Решение задач на построение изображений в линзах
Слайды и текст этой онлайн презентации
Слайд 1

Параллелепипед. Задачи на построение сечений.
Слайд 2

Цель работы:
Развитие пространственных представлений.
Задачи: Познакомить с правилами построения сечений. Выработать навыки построения сечений тетраэдра и параллелепипеда при различных случаях задания секущей плоскости. Сформировать умение применять правила построения сечений при решении задач по темам «Многогранники».
Задачи: Познакомить с правилами построения сечений. Выработать навыки построения сечений тетраэдра и параллелепипеда при различных случаях задания секущей плоскости. Сформировать умение применять правила построения сечений при решении задач по темам «Многогранники».
Слайд 3

Четырёхугольники АВВ1А1, ВСС1В1, СDD1C1, DAA1D1 также являются параллелограммами, т.к. каждый из них имеет попарно параллельные противоположные стороны (в четырёхугольнике АВВ1А1 стороны АА1 и ВВ1 параллельны по условию, а стороны АВ и А1В1 - по свойству линий пересечения двух параллельных плоскостей третьей.
А
В
D
С
А1
В1
C1
D1
Содержание
Далее
Параллелепипед
А
В
D
С
А1
В1
C1
D1
Содержание
Далее
Параллелепипед
Слайд 4

Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырёх параллелограммов, называется параллелепипедом и обозначается так: ABCDA1B1C1D1.
Параллелограммы, из которых составлен параллелепипед, называются гранями, их стороны - рёбрами, а вершины параллелограммов - вершинами параллелепипеда.
Далее
Содержание
Определения
Далее
Содержание
Определения
Слайд 5

Параллелепипед имеет шесть граней, двенадцать рёбер и восемь вершин.
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих рёбер - противоположными.
Далее
Содержание
Определения
Далее
Содержание
Определения
Слайд 6

На рисунке противоположными являются грани ABCD и A1B1C1D1, ABB1A1 и DCC1D1, ADD1A1 и BCC1B1. Две вершины, не принадлежащие одной грани, называются противоположными.
Далее
Содержание
Далее
Содержание
Слайд 7

Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.
Каждый параллелепипед имеет четыре диагонали. На рисунке диагоналями являются отрезки AC1, BD1, CA1 и DB1.
Содержание
Далее
Содержание
Далее
Слайд 8

Часто выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани - боковыми гранями параллелепипеда.
Рёбра параллелепипеда, не принадлежащие основаниям, называются боковыми рёбрами. Если выбрать грани ABCD и A1B1C1D1, то боковыми гранями будут параллелограммы, а боковыми рёбрами - отрезки AA1, BB1, CC1 и DD1.
Далее
Содержание
Далее
Содержание
Слайд 9

1.Противоположные грани параллелепипеда параллельны и равны.
Далее
В содержание
Свойства параллелепипеда
Далее
В содержание
Свойства параллелепипеда
Слайд 10
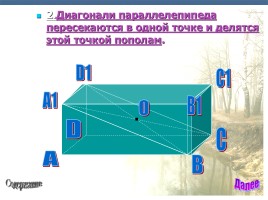
2.Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Далее
Содержание
Далее
Содержание
Слайд 11
Для решения многих геометрических задач необходимо строить сечения многогранников различными плоскостями.
Слайд 12

Понятие секущей плоскости
Секущей плоскостью параллелепипеда (тетраэдра) называется любая плоскость, по обе стороны от которой имеются точки данного параллелепипеда (тетраэдра).
Секущей плоскостью параллелепипеда (тетраэдра) называется любая плоскость, по обе стороны от которой имеются точки данного параллелепипеда (тетраэдра).
Слайд 13
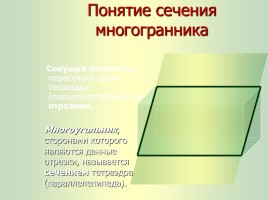
Многоугольник, сторонами которого являются данные отрезки, называется сечением тетраэдра (параллелепипеда).
Понятие сечения многогранника
Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам.
Понятие сечения многогранника
Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам.
Слайд 14

Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками.
Слайд 15

1. Соединять можно только две точки, лежащие в плоскости одной грани.
2. Секущая плоскость пересекает параллельные грани по параллельным отрезкам.
Правила построения сечений
Правила построения сечений
Слайд 16

3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку.
Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.
Правила построения сечений
Правила построения сечений
Слайд 17
Тетраэдр
Слайд 18

Тетраэдр - простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Тетраэдр, у которого все грани —равносторонние треугольники, называется правильным. Тетра́эдр (др.-греч.τετρά-εδρον — четырёхгранник
Тетраэдр
Тетраэдр
Слайд 19

тетраэдр
огонь
огонь
Слайд 20
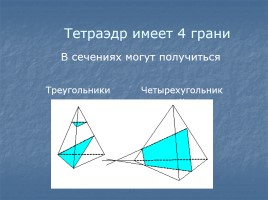
В сечениях могут получиться
Четырехугольники
Треугольники
Тетраэдр имеет 4 грани
Четырехугольники
Треугольники
Тетраэдр имеет 4 грани
Слайд 21
Куб (параллелепипед)
Слайд 22

Куб (параллелепипед)
Куб - правильный многогранник, каждая грань которого представляет собой квадрат. Общее число граней – 6; Общее число вершин – 8; Общее число рёбер – 12; Куб (др.-греч. κύβος) или правильный гексаэдр («правильный шестигранник»)
Куб - правильный многогранник, каждая грань которого представляет собой квадрат. Общее число граней – 6; Общее число вершин – 8; Общее число рёбер – 12; Куб (др.-греч. κύβος) или правильный гексаэдр («правильный шестигранник»)
Слайд 23

куб
земля
земля
Слайд 24
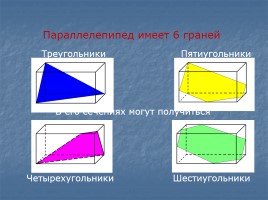
В его сечениях могут получиться
Параллелепипед имеет 6 граней
Параллелепипед имеет 6 граней
Слайд 25

МЕТОД СЛЕДОВ
Суть метода: построение вспомогательной прямой, являющейся линией пересечения секущей плоскости с плоскостью грани фигуры.
Эту линию называют следом секущей плоскости.
Суть метода: построение вспомогательной прямой, являющейся линией пересечения секущей плоскости с плоскостью грани фигуры.
Эту линию называют следом секущей плоскости.
Слайд 26

Построение сечений тетраэдра и параллелепипеда
Слайд 27
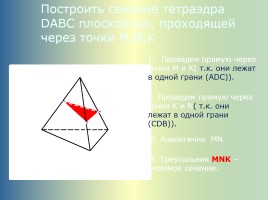
Построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K
Проведем прямую через точки М и К( т.к. они лежат в одной грани (АDC)).
2. Проведем прямую через точки К и N( т.к. они лежат в одной грани (СDB)).
3. Аналогично MN.
4. Треугольник MNK – искомое сечение.
Проведем прямую через точки М и К( т.к. они лежат в одной грани (АDC)).
2. Проведем прямую через точки К и N( т.к. они лежат в одной грани (СDB)).
3. Аналогично MN.
4. Треугольник MNK – искомое сечение.
Слайд 28
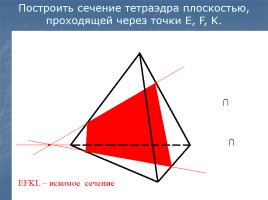
Построить сечение тетраэдра плоскостью, проходящей через точки E, F, K.
E
F
K
L
A
B
C
D
M
1. Проводим КF.
2. Проводим FE.
3. Продолжим EF, продол- жим AC.
5. Проводим MK.
7. Проводим EL
EFKL – искомое сечение
E
F
K
L
A
B
C
D
M
1. Проводим КF.
2. Проводим FE.
3. Продолжим EF, продол- жим AC.
5. Проводим MK.
7. Проводим EL
EFKL – искомое сечение
Слайд 29

A1
А
В
В1
С
С1
D
D1
Построить сечение параллелепипеда плоскостью, проходящей через точки M,A,D
М
1. AD
2. MD
3. ME//AD, т.к. (ABC)//(A1B1C1)
4. AE
5. AEMD – искомое сечение
E
А
В
В1
С
С1
D
D1
Построить сечение параллелепипеда плоскостью, проходящей через точки M,A,D
М
1. AD
2. MD
3. ME//AD, т.к. (ABC)//(A1B1C1)
4. AE
5. AEMD – искомое сечение
E
Слайд 30
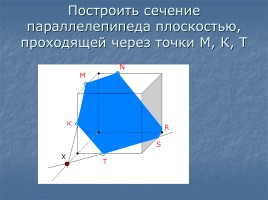
Построить сечение параллелепипеда плоскостью, проходящей через точки М, К, Т
М
К
Т
М
К
Т
Слайд 31
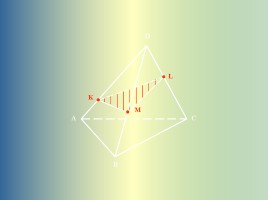
K
L
M
A
B
C
D
L
M
A
B
C
D
Слайд 32
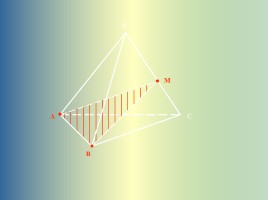
A
B
M
D
C
B
M
D
C
Слайд 33
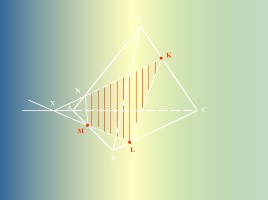
K
L
M
X
N
A
B
C
D
L
M
X
N
A
B
C
D
Слайд 34
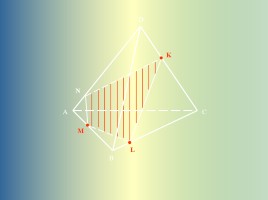
K
L
M
N
A
B
C
D
L
M
N
A
B
C
D
Слайд 35
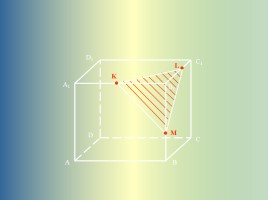
K
L
M
A
B
C
D
A1
B1
C1
D1
L
M
A
B
C
D
A1
B1
C1
D1
Слайд 36
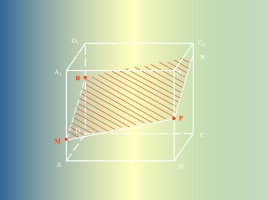
M
R
P
N
A
B
C
D
A1
B1
C1
D1
R
P
N
A
B
C
D
A1
B1
C1
D1
Слайд 37
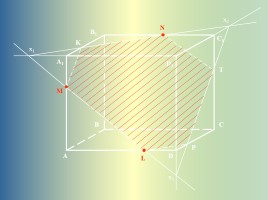
A
A1
B
B1
C
C1
D
D1
M
N
L
x1
x2
x3
K
T
P
A1
B
B1
C
C1
D
D1
M
N
L
x1
x2
x3
K
T
P
Слайд 38
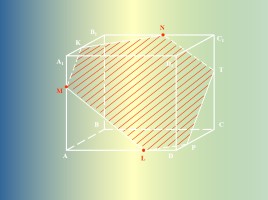
A
A1
B
B1
C
C1
D
D1
M
N
L
K
T
P
A1
B
B1
C
C1
D
D1
M
N
L
K
T
P
Слайд 39
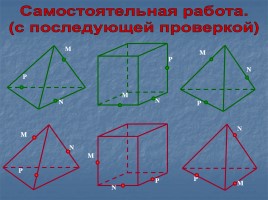
Самостоятельная работа.
(с последующей проверкой)
Слайд 40
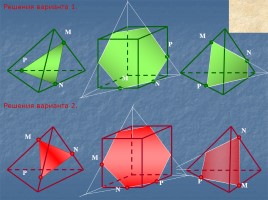
M
N
P
M
N
P
M
N
P
Решения варианта 1.
Решения варианта 2.
M
N
P
M
N
P
M
N
P
N
P
M
N
P
M
N
P
Решения варианта 1.
Решения варианта 2.
M
N
P
M
N
P
M
N
P
Слайд 41

Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их
(Д. Пойа)
СПАСИБО ЗА УРОК !
СПАСИБО ЗА УРОК !
Слайд 42

Домашняя работа
П.13,14 №76,104.
П.13,14 №76,104.
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
