Презентация - Решение задач на классическое определение вероятности

ЕГЭ. Математика. (Профильный уровень. Задание 4 Базовый уровень. Задание 10)
(Теория вероятности. Классическое определение вероятности)
Учитель математики ФГКОУ СОШ № 8 г. Севастополя Павленко Марина Петровна

Теория. Вероятность — это числовая характеристика возможности наступления какого-либо события. Вероятностью события А называется отношение числа m случаев, благоприятствующих его наступлению, к числу n всех возможных случаев.
P(A) – вероятность события А
m – число случаев, при которых событие А наступает
n – число всех возможных случаев

Теория. Если событие наступить не может, оно называется невозможным.
Если событие непременно наступает, оно называется достоверным.
Вероятность события – число из отрезка [0; 1]

Теория. Два события называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события называются зависимыми.
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании. В противном случае события называются несовместными.
Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Вероятности противоположных событий в сумме дают 1.

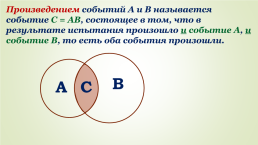
Произведением событий А и В называется событие С = AB, состоящее в том, что в результате испытания произошло и событие А, и событие В, то есть оба события произошли.
B
C
A

Вероятность произведения двух независимых событий A и B равна произведению этих вероятностей
P (AB) = P (A) ∙ P (B)

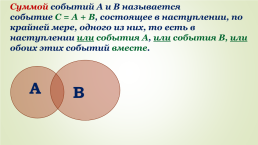
Суммой событий А и В называется событие С = А + В, состоящее в наступлении, по крайней мере, одного из них, то есть в наступлении или события А, или события В, или обоих этих событий вместе.
A
B

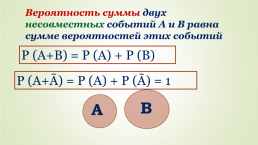
Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий
P (A+B) = P (A) + P (B)
P (A+Ā) = P (A) + P (Ā) = 1
B
A

1. (Задача об игральных костях). В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
.1.2.3.4.5.6
1......
2......Х
3.....Х.
4....Х..
5...Х...
6..Х....
n = 6 ∙ 6 = 36
m = 5

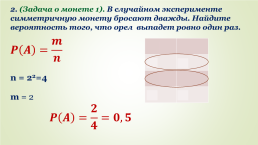
2. (Задача о монете 1). В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
О.О
О.Р
Р.О
Р.Р
n = 22=4
m = 2

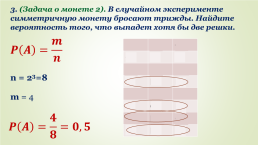
3. (Задача о монете 2). В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что выпадет хотя бы две решки.
О.О.О
О.О.Р
О.Р.О
О.Р.Р
Р.О.О
Р.О.Р
Р.Р.О
Р.Р.Р
n = 23=8
m = 4

4. (Задача о сумках). Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых
n = 100+8=108
m = 100

5. (Задача о бытовых приборах). В большой партии насосов в среднем на каждые 1992 исправных 8 неисправных насосов. Найдите вероятность того, что случайно выбранный насос окажется неисправным.
n = 1992+8=2000
m = 8

6. (Задача о спортсменах ). В соревнованиях по толканию ядра участвуют 6 спортсменов из Великобритании, 3 спортсмена из Франции, 6 спортсменов из Германии и 10 – из Италии. Порядок в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Франции
n = 6 + 3 + 6 +10 =25
m = 3

7. (Задача о научной конференции). Научная конференция проводится в 5 дней. Всего запланировано 75 докладов – в первые 3 дня по 17 докладов, и остальные распределены поровну между четвертым и пятым днем. Порядок докладов распределяется жеребьевкой. Какова вероятность того, что доклад профессора Максимова запланирован на последний день конференции?
n = 75
m = (75 – 3 ∙ 17) : 2

8. (Задача о фестивале). На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
n = 6
Д.Ш.Н
Д.Н.Ш
Н.Д.Ш
Н.Ш.Д
Ш.Д.Н
Ш.Н.Д
m = 2

9. (Задача о экзаменационных билетах). В сборнике билетов по истории всего 20 билетов, в 12 из них встречается вопрос по теме «Смутное время». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос по теме «Смутное время»
m = 20 – 12 = 8
n = 20

10. (Задача о туристах). В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
n = 30
Сколько всего туристов?
Сколько туристов могут полететь первым рейсом?
m = 6

11. (Задача о чемпионате мира). В чемпионате мира участвуют 12 команд. С помощью жребия их нужно разделить на четыре группы по три команды в каждой. В ящике вперемешку лежат карточки с номерами групп. 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4 Капитаны команд тянут по одной карточке. Какова вероятность того, что команды Канады окажется в третьей группе?
n = 12
m = 3

12. (Задача о друзьях). В классе 26 учащихся, среди них два друга — Андрей и Сергей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
n = 26 – 1 =25
12+А
m = 12

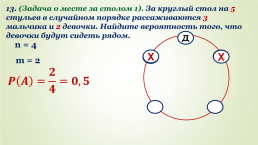
13. (Задача о месте за столом 1). За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом.
Д
n = 4
X
X
m = 2

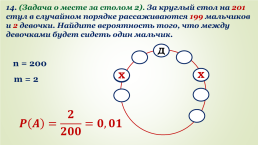
14. (Задача о месте за столом 2). За круглый стол на 201 стул в случайном порядке рассаживаются 199 мальчиков и 2 девочки. Найдите вероятность того, что между девочками будет сидеть один мальчик.
Д
n = 200
Х
Х
m = 2

15. (Задача об игральных костях). Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию А - «Сумма очков равна 7».
.1.2.3.4.5.6
1.2.3.4.5.6.7
2.....7.
3....7..
4...7...
5..7....
6.7.....
m = 6

16. (Задача о частоте рождения). В некотором городе из 2000 появившихся на свет младенцев 1020 мальчики. Найдите частоту рождения девочек в этом городе
n = 2000
m = 2000 – 1020 = 980

17. (Задача о деньгах в кармане). У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
n = 25
Всего монет: 12+6+4+3 = 25
Сумма денег составляет: 12∙1+6∙2+4∙5+3∙10 = 74 р.
Какие монеты можно взять, чтобы оставшаяся сумма была больше 70 р?
m = 12+6

18. (Задача о часах). Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 10, но не дойдя до отметки 1.
n = 12
m = 3

19. (Задача о бытовых приборах). Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
0,051 – 0 ,045 = 0,006

Теория. Два события называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события называются зависимыми.

Вероятность произведения двух независимых событий A и B равна произведению этих вероятностей
P (AB) = P (A) ∙ P (B)

20. (Задача о шахматистах). Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
S – А играет белыми и выигрывает
T – А играет черными и выигрывает
S и T – независимые события

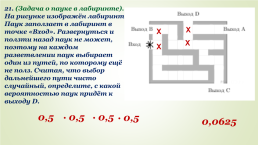
21. (Задача о пауке в лабиринте). На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.
X
X
X
X
∙ 0,5
∙ 0,5
0,5
∙ 0,5
0,0625

22. (Задача о биатлонисте). Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист первые 3 раза попал в мишени, а последний раз промахнулся. Результат округлите до десятых.
Р (попал) = 0,7
Р (не попал) = 0,3
0,7 ∙ 0,7 ∙ 0,7 ∙ 0,3 =0,1029

23 . (Задача о лампочках). Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,27. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Р (перегорит 1 лампа) = 0,27
Р (перегорит 2 лампа) = 0,27
Р (обе лампы перегорят) = 0,27 ∙ 0,27 = 0,0729
Р (хотя бы одна не перегорит) = 1 - 0,0729

24. (Задача о подшипниках). При изготовлении подшипников диаметром 61 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,976. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 60,99 мм, или больше, чем 61,01 мм.

1. (Задача о цифрах на телефоне). На клавиатуре телефона 10 цифр от 0 до 9. Какова вероятность того, что случайно нажатая цифра, будет четной и больше трех.
n = 10
m = 3
0,3

25. (Задача о температуре тела). Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже, чем 36,8°, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8° или выше.

Спасибо за внимание!!!