Презентация - Решение уравнений с модулями

Решение уравнений с модулями
Выполнила: ученица 11 класса Бугреева Ангелина

Актуальность работы:
Уравнения с модулями, нередко встречаются на математических олимпиадах, вступительных экзаменах в институты и на ЕГЭ. Несмотря на все это, программой школьного курса математики уделяется не достаточно времени этой теме. Объект исследования: Уравнения с модулями

Цель работы:
узнать какие существуют способы и виды решения уравнений с модулями. Задачи: 1.Изучить виды уравнений с модулями 2.Изучить свойства модулей. 3.Изучить способы решения уравнений, содержащих модуль. 4.Решить каждый вид уравнения с модулем всеми способами, если это возможно

Гипотеза:
Для решения уравнений с модулями существуют различные способы их решения. Я предполагаю, что существует ли универсальный способ решения подходящий для всех уравнений.

Основные понятия:
Геометрическое определение: Модулем числа   A  называют расстояние (в единичных отрезках) от начала координат до точки Алгебраическое определение: Модуль числа а или абсолютная величина числа а равна а, если а больше или равна нулю или равна –а, если а меньше нуля. Вид записи: |a| = a, если a ≥ 0 и |a| = -a, если a < 0
а
а
-а 0 а

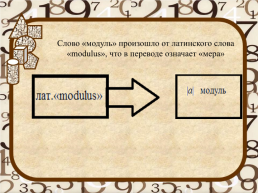
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера»

Свойства модуля:
1. ǀаǀ ≥ 0 2. ǀаǀ = ǀ-аǀ 3. ǀаǀ ≥ а 4. ǀаbǀ = ǀаǀ ǀbǀ 5. ǀа?ǀ = ǀаǀǀ?ǀ , b ǂ 0 6. ǀа + bǀ ≤ ǀаǀ + ǀbǀ 7. ǀа + bǀ = ǀаǀ + ǀbǀ, аb ≥ 0 8. ǀаǀ + ǀbǀ = а + b, а ≥ 0 и b ≥ 0 9. ǀа - bǀ = ǀаǀ + ǀbǀ, аb ≤ 0 10. ǀаǀ - ǀbǀ ≥ 0, а² - b² ≥ 0

Виды решения уравнений, содержащих модуль:

1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы: {±c, если с > 0 Если |x| = c, то x = {0, если с = 0 {нет корней, если с < 0

Примеры:
1) |x| = 7, т.к. 7 > 0, то x = ±7; 2) |x| = -7, т.к. -7 < 0, то уравнение не имеет корней; 3) |x| = 0, то x = 0.

2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b< 0, решений не будет.

Примеры:
1) |x + 5| = 7, т.к. 7 > 0, то x + 5 = 7 или x + 5 = -7 x = 2            x = -12 Ответ: -12; 2 2) |x2 – 4| = 12, т.к. 12 > 0, то x2 – 4 = 12 или x2 – 5 = -12 x2 = 16           x2 = -7 x = ± 4             нет корней Ответ: ± 4  3) |x2 – 5x| = -8 , т.к. -8 < 0, то уравнение не имеет корней.

3. Уравнение вида |f(x)| = g(x). Такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь: f(x) = g(x) или f(x) = -g(x).

Примеры:
|x – 9| = 6x – 12. Данное уравнение будет иметь корни, если 6x – 12 ≥ 0. Именно с этого и начинают решение таких уравнений. 1. Допустимые значения 6x – 12 ≥ 0 6x ≥ 12 x ≥ 2. 2. Решение: x –9 = 6x – 12 или x – 9 = -(6x – 12) -5x = -3                     7x = 21 x = 3/5                      x = 3 3. Объединяем допустимые значения . и решение, получаем: Корень x =3/5 не подходит по допустимым значениям, он меньше 2, а x = 3 этому условию удовлетворяет. Ответ: 3

4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям  f(x) = g(x) или f(x) = -g(x).

Примеры:
1) |x2 – 3x + 2| = |3x – 6|. Данное уравнение равносильно двум следующим: x2 – 3x + 2  = 3x – 6 или x2 – 3x +2  = -3x + 6 x2 – 6x + 8  = 0            x2 + 2 = 6 x = 2 или x = 4             x = 2 или x = -2 Ответ:-2;2;4.

5. Уравнения, решаемые способом подстановки (замены переменной).

Примеры:
x2 – 9|x| + 8 = 0. x2 = |x|2, поэтому уравнение можно переписать  так: |x|2 – 9|x| + 8 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь: t2 – 9t + 8 = 0. Решая данное уравнение, получаем, что t = 1 или t =8. Вернемся к замене: |x| = 1 или |x| = 8 x = ±1        x = ± 8 Ответ: -8;-1;1;8.

Способы решения уравнений содержащих модуль. Основные понятия

1  способ. Метод последовательного раскрытия модуля.
Пример 1. Решим уравнение |х-7|=4. Произведем следующие рассуждения. Если выражение, стоящее под знаком модуля неотрицательно, то есть х-7≥0, то уравнение примет вид х-7=4. Если значение выражения под знаком модуля отрицательно, то по определению оно будет равно – (х-7)=4 или х-7= -4. Решая полученные уравнения, находим: х1=3, х2=11. Ответ: 3; 11.
|a|= a, если а ≥ 0 |a|= -a, если а < 0

Пример 2. Решим уравнение ||2х-1|-4|=6. 1) |2х-1|-4=6, |2х-1|=10. Используя еще раз определение модуля, получим: 2х-1=10 либо 2х-1= -10. Откуда х1=5,5, х2= -4,5. 2) |2х-1|-4= -6, |2х-1|= -2. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен. Ответ:-4,5;5,5

2 способ. Метод интервалов.  Метод интервалов – это метод разбиения числовой прямой на промежутки, в которых по определению модуля знак абсолютной величины можно будет снять. Для каждого из промежутков необходимо решить уравнение и сделать вывод относительно получившихся корней. Корни, удовлетворяющие промежуткам, и дадут окончательный ответ.

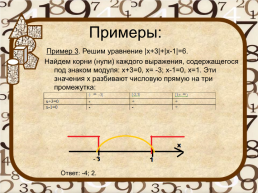
Примеры:
Пример 3. Решим уравнение |х+3|+|х-1|=6. Найдем корни (нули) каждого выражения, содержащегося под знаком модуля: х+3=0, х= -3; х-1=0, х=1. Эти значения х разбивают числовую прямую на три промежутка:
-
Ответ: -4; 2.

3 способ. Графический метод. Суть данного метода заключается в использовании графиков функций для нахождения корней уравнения. Этот метод реже других применяют для решения уравнений, содержащих модуль, так как, во-первых, он занимает достаточно много времени и не всегда рационален, а, во-вторых, результаты, полученные при построении графиков, не всегда являются точными.

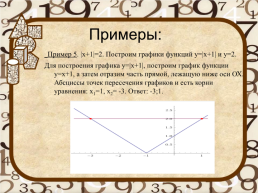
Примеры:
Пример 5. |х+1|=2. Построим графики функций у=|х+1| и у=2. Для построения графика у=|х+1|, построим график функции у=х+1, а затем отразим часть прямой, лежащую ниже оси ОХ. Абсциссы точек пересечения графиков и есть корни уравнения: х1=1, х2= -3. Ответ: -3;1.

4 способ. Метод решения при помощи зависимостей между числами а и в, их модулями и квадратами этих чисел.  |а|=|в|  а=в или а=-в;  а2=в2  а=в или а=-в; (1) |а|=|в|   а2=в2 (2)

Примеры:
Пример 6. Решим уравнение |х2-10х+5|=|х2-5|. Учитывая соотношение (1), получим: х2-10х+5= х2-5 или х2-10х+5= -х2+5 х=1 х=0 или х=5. Ответ: 0;1;5.

5 способ. Использование геометрической интерпретации модуля.  Опорная информация: геометрический смысл модуля разности величин – это расстояние между ними. Например, геометрический смысл выражения |х-а| - длина отрезка координатной оси, соединяющей точки с абсциссами а и х. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений.

Примеры:
Пример 7. |х+3|=|х-9|. В силу соотношения (2) получаем: (х+3)2=(х-9)2; х2+6х+9= х2-18х+81; х=3 Ответ:3 Пример 8. (3-2х)2=(х-6)2. Учитывая соотношение (2), получаем: |3-2х|=|х-6|, откуда из соотношения (1), имеем: 3-2х=х-6 или 3-2х=-(х-6) х=3 х=-3. Ответ: -3; 3.

Вывод:
В начале данного исследования была поставлена цель, изучить решение уравнений с модулями. Для достижения этой цели были рассмотрены виды уравнений, содержащих модуль, их свойства и способы решения, были выявлены достоинства и недостатки

https://yravneniyawithmodule

https://yravneniyawithmodule

Список литературы
https://nsportal.ru/shkola/algebra/library/2011/06/19/metodicheskie-rekomendatsii-po-teme-reshenie-uravneniy-s-modulem-v http://nenuda.ru https://infourok.ru/sposobi-resheniya-uravneniy-soderzhaschih-modul-398462.html Галицкий М.Л.,Гольдман А.М.,Звавич Л.И.Сборник задач по алгебре для 8-9 классов:Учебное пособие для учащихся школ и классов с углубленным изучение математики.-М.:Просвещение,1994-271с Алгебра и начала анализа:Учебник для 10 класса общеобразовательных учреждений/С.М.Никольский, М.К.Потапов Н.Н. Решетников, А.В.Шевкин.- М.:Просвещение,2001-381с Алгебра и начала анализа:Учебник для 11 класса общеобразовательных учреждений/С.М.Никольский, М.К.Потапов Н.Н. Решетников, А.В.Шевкин.- М.:Просвещение,2002-448с Доброва О.Н. Задания по алгебре и математическому анализу:пособие для учащихся 9-11 классов общеобразовательных учреждений.- М.:Просвещение,1996-351с Углубленное изучение алгебры и математического анализа:Методические рекомендации и дидактические материалы :Пособие для учителя М.:Просвещение,1997-350с

СПАСИБО ЗА ВНИМАНИЕ!