Презентация - Развитие критического мышления на уроках математики в условиях реализации ФГОС

Мастер-класс « Развитие критического мышления на уроках математики в условиях реализации ФГОС».

Критика – изучение или обсуждение чего-либо с целью поиска недостатков. С.И. Ожегов

Мышление – это творческий познавательный процесс, обобщенно и опосредствованно отражающий отношения предметов и явлений, законы объективного мира.

Критическое мышление – это умение занять свою позицию по обсуждаемому вопросу и умение обосновать её способность выслушать собеседника, тщательно обдумать аргументы и проанализировать их логику.

Технология «Развитие критического мышления» разработана в конце XX века в США и связана с именами Чарльза Темпла, Джинни Стила, Куртис Мередита, а в России – М.В.Клариным, С.И.Заир-Беком, И.О.Загашевым, И.В.Муштавинской и красноярскими учеными и практиками А.Бутенко, Е.Ходос.

Технология «Развитие критического мышления» - это целостная система, которая развивает продуктивное творческое мышление, формирует интеллектуальные умения, навыки работы с информацией, учит учиться. (по Выготскому).

Критическое мышление есть мышление самостоятельное Информация является отправным, а отнюдь не конечным пунктом критического мышления. Критическое мышление начинается с постановки вопросов и уяснения проблем, которые нужно решить. Критическое мышление стремится к убедительной аргументации. Критическое мышление есть мышление социальное.

Формирует собственное мнение Совершает обдуманный выбор между различными мнениями Решает проблемы Аргументировано спорит Ценит совместную работу, в которой возникает общее решение Умеет ценить чужую точку зрения и сознает, что восприятие человека и его отношение к любому вопросу формируется под влиянием многих факторов.

Цель данной технологии - развитие мыслительных навыков учащихся, необходимых не только в учебе, но и в обычной жизни (умение принимать взвешенные решения, работать с информацией, анализировать различные стороны явлений и т.п.).

Базовая модель технологии КМ предлагает 3 стадии:
Вызов (учащиеся должны использовать свои предыдущие знания по теме,  делать прогнозы по содержанию предстоящей информации) Осмысление новой информации(учащиеся интегрируют идеи, изложенные в тексте, со своими собственными идеями)  Рефлексия (интерпретация обретённых идей и информации собственными словами).

Приемы технологии критического мышления

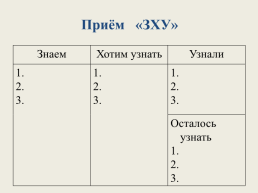
Приём «ЗХУ»
Знаем.Хотим узнать.Узнали
1. 2. 3..1. 2. 3..1. 2. 3.
Осталось узнать 1. 2. 3.

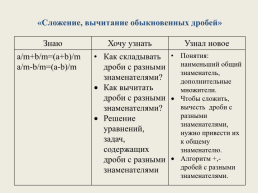
«Сложение, вычитание обыкновенных дробей»
Знаю.Хочу узнать.Узнал новое
а/m+b/m=(a+b)/m а/m-b/m=(a-b)/m.Как складывать дроби с разными знаменателями? Как вычитать дроби с разными знаменателями? Решение уравнений, задач, содержащих дроби с разными знаменателями.Понятия: наименьший общий знаменатель, дополнительные множители. Чтобы сложить, вычесть дроби с разными знаменателями, нужно привести их к общему знаменателю. Алгоритм +,- дробей с разными знаменателями.

«Площадь параллелограмма»
З.Х.У
Единицы измерения площади: мм², см², дм², м², км². Sквадрата = а·а=а² Sпрямоуг .= а·в.Формулы для вычисления площади треугольника, параллелограмма, трапеции, ромба..Определение площади Свойства площади Док-во формулы: S=a∙b Sпараллелограмма S=a∙h Осталось узнать: Sтрапеции Sромба Потренироваться в применении формул в различных ситуациях

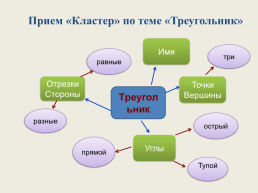
Прием «Кластер» по теме «Треугольник»
Имя
три
равные
Отрезки Стороны
Точки Вершины
Треугольник
разные
острый
Углы
прямой
Тупой

Кластер по теме «Квадратные уравнения»
Неполное квадратное уравнение
Неприведённое квадратное уравнение
Полное квадратное уравнение
Приведённое квадратное уравнение
Квадратные уравнения
Неполное квадратное уравнение (c = 0)
Неполное квадратное уравнение (b = 0)
Неполное квадратное уравнение (b=c= 0)
3х – 5х + 2 = 0
5х = 0
3х – 2х = 0
4х + 5х + 1 = 0
Х + 3х + 2 = 0
х – 3х + 1 = 0
х – 3 = 0
0,2х – 2х = 0

Прием «Верные и неверные утверждения" или "верите ли вы" «Понятие вектора в пространстве»

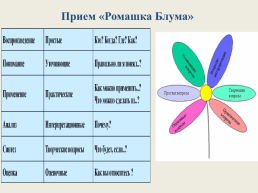
Прием «Ромашка Блума»

Особенности работы с различными видами текста
Приём Инсерт (insert) I – interactive: самоактивизирующая N – noting: разметка S – system: системная E – effective: для эффективного R – reading чтения и T – thinking размышления

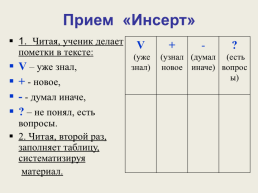
Прием «Инсерт»
1. Читая, ученик делает пометки в тексте: V – уже знал, + - новое, - - думал иначе, ? – не понял, есть вопросы. 2. Читая, второй раз, заполняет таблицу, систематизируя материал.
V (уже знал).+ (узнал новое.- (думал иначе).? (есть вопросы)
...

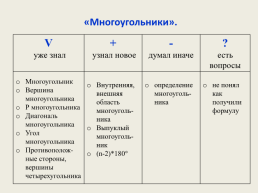
«Многоугольники».
V уже знал.+ узнал новое.- думал иначе.? есть вопросы
Многоугольник Вершина многоугольника Р многоугольника Диагональ многоугольника Угол многоугольника Противополож-ные стороны, вершины четырехугольника.Внутренняя, внешняя область многоуголь-ника Выпуклый многоуголь-ник (n-2)*180°.определение многоуголь-ника.не понял как получили формулу

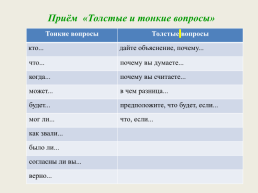
Приём «Толстые и тонкие вопросы»
Тонкие вопросы.Толстые вопросы
кто....дайте объяснение, почему...
что....почему вы думаете...
когда....почему вы считаете...
может....в чем разница...
будет....предположите, что будет, если...
мог ли....что, если...
как звали....
было ли....
согласны ли вы....
верно....

Прием «Составление «Синквейна»»
Для его написания существуют правила:
Название.существительное -1
Описание.Прилагательное - 2
Действия.Глагол - 3
Чувство.Фраза из 4 слов
Повторение сути.(синоним) 1 слово

Уравнение Линейное квадратное Решить найти доказать Равенство, содержащее переменную Корень

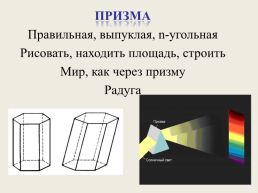
Призма Правильная, выпуклая, n-угольная Рисовать, находить площадь, строить Мир, как через призму Радуга

Прием «Пазл»
Пример. Тема “Параллельные прямые”, 7 класс. Каждая теорема в этом комплекте представлена так: 1-я карточка – словесная формулировка, 2-я карточка – чертеж к теореме, 3-я карточка – краткая запись условия и заключения теоремы, Ученику надо полностью собрать указанную ему теорему

Ценность данной технологии  и в том, что она учит: - детей слушать и слышать, - развивает речь, - даёт возможность общения, - активизирует мыслительную деятельность, познавательный интерес, - побуждает детей к действию, поэтому работают все. Уходит страх, повышается ответственность ученика за свой ответ, учитель и учащиеся вместе участвуют в добывании знаний. Всё это необходимо не только на уроке математики. В этом заключается метапредметность данной технологии и её значимость.

Спасибо за внимание!