Презентация - Организация современного урока математики в средних и старших классах в условиях реализации ФГОС

Организация современного урока математики в средних и старших классах в условиях реализации ФГОС.
Антонова Татьяна Викторовна МБОУ «Инсарская СОШ №1», г. Инсар, Республика Мордовия

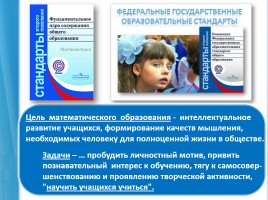
Цель математического образования - интеллектуальное развитие учащихся, формирование качеств мышления, необходимых человеку для полноценной жизни в обществе.
Задачи – … пробудить личностный мотив, привить познавательный интерес к обучению, тягу к самосовер-шенствованию и проявлению творческой активности, "научить учащихся учиться".

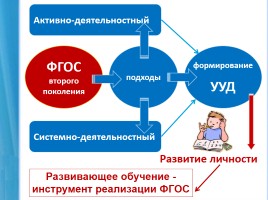
ФГОС второго поколения
подходы
УУД
формирование
Активно-деятельностный
Системно-деятельностный
Развитие личности
Развивающее обучение - инструмент реализации ФГОС

Обучение, которое, обеспечивая полноценное усвоение знаний, формирует учебную деятельность и тем самым непосредственно влияет на умственное развитие, и есть развивающее обучение. И.С. Якиманская Цель развивающего обучения – развитие личности учащегося, превращение его в субъект учения и собственной жизни. Результат заключаются не в изменении предмета, с которым действует ученик, а в изменении последним самого себя в ходе учебной деятельности.

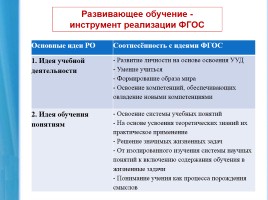
Основные идеи РО Соотнесённость с идеями ФГОС
1. Идея учебной деятельности - Развитие личности на основе освоения УУД - Умение учиться - Формирование образа мира - Освоение компетенций, обеспечивающих овладение новыми компетенциями
2. Идея обучения понятиям - Освоение системы учебных понятий - На основе усвоения теоретических знаний их практическое применение - Решение значимых жизненных задач - От изолированного изучения системы научных понятий к включению содержания обучения в жизненные задачи - Понимание учения как процесса порождения смыслов
Развивающее обучение - инструмент реализации ФГОС

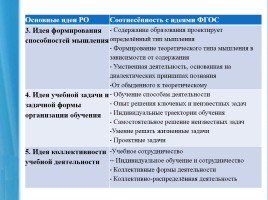
Основные идеи РО Соотнесённость с идеями ФГОС
3. Идея формирования способностей мышления - Содержание образования проектирует определённый тип мышления - Формирование теоретического типа мышления в зависимости от содержания - Умственная деятельность, основанная на диалектических принципах познания -От обыденного к теоретическому
4. Идея учебной задачи и задачной формы организации обучения - Обучение способам деятельности - Опыт решения ключевых и неизвестных задач - Индивидуальные траектории обучения - Самостоятельное решение неизвестных задач -Умение решать жизненные задачи - Проектные задачи
5. Идея коллективности учебной деятельности Учебное сотрудничество - Индивидуальное обучение и сотрудничество - Коллективные формы деятельности - Коллективно-распределённая деятельность

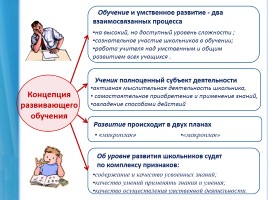
на высокий, но доступный уровень сложности ; сознательное участие школьников в обучении; работа учителя над умственным и общим развитием всех учащихся .
активная мыслительная деятельность школьника, самостоятельное приобретение и применение знаний, овладение способами действий
«микроплан»
«макроплан»
содержание и качество усвоенных знаний; качество умений применять знания и умения; качество осуществления умственной деятельности.
Об уровне развития школьников судят по комплексу признаков:

Условия повышения развивающего эффекта обучения
а) формирование предметных знаний и умений; б) формирование приемов умственной деятельности; в) овладение рациональными приемами учебной работы; г) применение активных методов и форм обучения.
Основой развивающего обучения является проблемное обучение.

Формирование предметных знаний и умений
Развивающая функция присуща:
понятиям и теориям школьного курса; предметным и общеучебным умениям и навыкам; методологическим знаниям (о знаниях, о методах их приобретения, а о способах самоорганизации деятельности); языку науки; прикладным аспектам содержания.
Учебные приемы, способствующие развитию личности:
перенос усвоенных знаний и способов действий в новую ситуацию; поиск новых способов деятельности; самоуправление учебной деятельностью; выполнение заданий на сравнение, классификацию, обобщение и др.

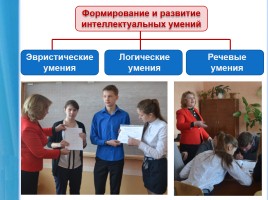
Формирование и развитие интеллектуальных умений
Эвристические умения
Логические умения
Речевые умения

Пример 1: Урок по теме «Сумма углов треугольника»
Проблемная ситуация (задание невыполнимое вообще): Постройте треугольник с углами 9000, 12000, 6000. Побуждающий диалог. Учитель: – Вы можете начертить такой треугольник? (Побуждение к осознанию противоречия.) Ученик: – Нет, не получается! (осознание затруднения.) Учитель: – Какой же вопрос возникает? (Побуждение к формулировке проблемы.) Ученик: – Почему не строится треугольник? (Проблема как вопрос, не совпадающий с темой урока.)  Формулировка учебной проблемы. Диалог, побуждающий к выдвижению и проверке гипотезы. – Начертите треугольник. – Измерьте его углы транспортиром. – Найдите сумму углов. – Какие результаты у вас получились? – К какому круглому числу приближаются ваши результаты? – Что же можно предположить о сумме углов треугольника? – Сверим вывод с учебником. – А почему у вас получились неточные результаты?

Пример 2: Исследовательская работа на уроке по теме «Признаки делимости на 3 и 9»
1. Представьте число 8535 в виде суммы разрядных слагаемых. 2. Каждое круглое число представьте в виде суммы двух слагаемых, одно из которых равно 1 (например: 100 = 99 + 1). 3. Раскройте скобки, применив распределительный закон a·(b + c) = ( a·c + b·c ). 4. Пользуясь законами сложения, упростите полученное выражение, заключив в скобки слагаемые, не входящие в произведения. Выполните сложение в скобках. 5. Будет ли данное выражение делится на 3, согласно свойствам делимости суммы и произведения? 6. Подумайте, от делимости на 3 какого слагаемого будет зависеть делимость всего выражения? 7. Как получилось это слагаемое? Что это за цифры? 8. Попробуйте сделать вывод о том, когда число делится на 3? Сформулируйте правило. 9. Проверьте свой вывод по учебнику.

Пример 3: Урок по теме « Формулы сокращенного умножения»
Прочитай выражения: (а-в)2; а2-в2; а2-2ав+в2. Найди значение выражения при а=4, в=1; а=-3, в=2; а=-1, в= -5 . Что ты замечаешь? Проверь свою гипотезу для произвольно выбранных значений а и в. Объясни полученный вывод, используя графическую модель. в а
(а-в)²
в²

Пример 4: Синквейны учащихся
Уравнения Сложные, красивые; Думать, терпеть, радоваться; Уравнения важнее политики, политика существует только для данного момента, а уравнения будут существовать вечно. Наука. Многочлен Стандартный, трудный; Умножать, складывать, трудиться; Многочлены описывают многие процессы в жизни, сложенные воедино. Сумма.

Пример 5: Составить математическую модель к задаче. Ни один полет не обходится без экспериментов, вот и вам предстоит выяснить: Влияние невесомости на рост грибов. Скорость роста гриба в теплую погоду на Земле равна 4мм/мин. На сколько бы вырос гриб и какова бы была его высота, если бы он рос с такой же скоростью 1час и его первоначальная высота была 10 мм? Какова была бы высота такого же гриба, в космических условиях, если скорость роста его на станции увеличивается в 2 раза. Какие перспективы этот эксперимент может дать на земле? Решение задачи может быть предложено в двух вариантах. Аналитическим способом и графическим способом.

Пример 6: Задачи на проценты
В 6 классе 25 человек, отличники составляют 25%, от хорошистов. На сколько процентов отличников в классе меньше, чем хорошистов?
В 6 классе 25 человек, отличники составляют 25%, от хорошистов. На сколько процентов хорошистов больше, чем отличников?

Графики зависимости
1.На одной координатной плоскости построй графики зависимостей у=-2х+1 и у=-2х-3. Что ты наблюдаешь? Сформулируй гипотезу. 2.На одной координатной плоскости построй графики зависимостей у=кх, при к=-1, к=-3, к=-1/3. Что ты наблюдаешь? Сформулируй гипотезу.

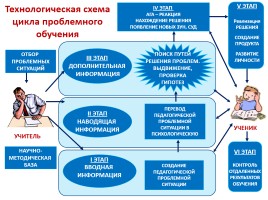
ОТБОР ПРОБЛЕМНЫХ СИТУАЦИЙ
НАУЧНО- МЕТОДИЧЕСКАЯ БАЗА
IV ЭТАП АГА – РЕАКЦИЯ НАХОЖДЕНИЕ РЕШЕНИЯ ПОЯВЛЕНИЕ НОВЫХ ЗУН, СУД
ПЕРЕВОД ПЕДАГОГИЧЕСКОЙ ПРОБЛЕМНОЙ СИТУАЦИИ В ПСИХОЛОГИЧЕСКУЮ
СОЗДАНИЕ ПЕДАГОГИЧЕСКОЙ ПРОБЛЕМНОЙ СИТУАЦИИ
ВВОДНАЯ ИНФОРМАЦИЯ
I ЭТАП
II ЭТАП НАВОДЯЩАЯ ИНФОРМАЦИЯ
III ЭТАП ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
УЧИТЕЛЬ
УЧЕНИК
ПОИСК ПУТЕЙ РЕШЕНИЯ ПРОБЛЕМ. ВЫДВИЖЕНИЕ, ПРОВЕРКА ГИПОТЕЗ
V ЭТАП Реализация РЕШЕНИЯ СОЗДАНИЕ ПРОДУКТА РАЗВИТИЕ ЛИЧНОСТИ
VI ЭТАП КОНТРОЛЬ ОТДАЛЕННЫХ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ
Технологическая схема цикла проблемного обучения

про урок

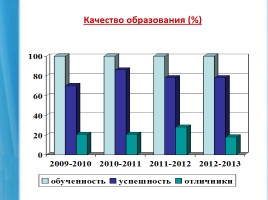
Качество образования (%)

Результаты применения РО
самореализация учащихся
мотивация к учению
понимание радости открытий
хороший уровень знаний
100% выбор элективных курсов
личностное развитие
призовые места в конкурсах
формирование компетентностей
призовые места в олимпиадах

Результаты применения РО

Школа – пространство мысли и творчества для будущего