Презентация - Домашнее задание по учебнику 6 класса:. Б: изучить § 22 (правила выучить, вопросы стр. 133-134), № 671, 673 П: № 675

Домашнее задание по учебнику 6 класса:
Б: Изучить § 22 (правила выучить, вопросы стр. 133-134), № 671, 673 П: № 675

12.01.2023
Классная работа
Прямая и обратная пропорциональности

Устная разминка(ответить на вопросы)
1. Равенство двух отношений называют … (продолжить предложение). 2. Отношение 2-х чисел показывает, во сколько раз первое число…. 3. Если пропорция верна, то произведение её средних членов равно произведению …. 4.Назовите крайние члены пропорции:7:21=1:3 5. Верна ли пропорция: 5:3 =2:1,2 ? 6.Частное двух чисел называют … (продолжить предложение). 7. Если пропорция верна, то произведение её крайних членов равно произведению … 8. Отношение двух чисел показывает, какую часть первое число ….

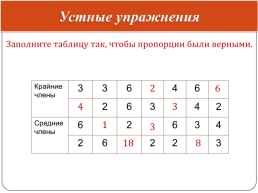
Устные упражнения
Заполните таблицу так, чтобы пропорции были верными.
Крайние члены.3.3.6..4.6.
.2.6.3..4.2
Средние члены.6..2..6.3.4
2.6..2.2..3

Определение прямо пропорциональных величин
Если две величины связаны между собой так, что с увеличением (уменьшением) одной в несколько раз вторая увеличивается (уменьшается) во столько же раз, то такие величины называются прямо пропорциональными.

Если две величины прямо пропорциональны, то отношение любых двух значений первой величины равно отношению соответствующих значений второй величины.
Примеры
– при постоянной скорости
– при постоянном времени

Прямо пропорциональные величины
Примеры прямо пропорциональных величин:
количество товара и его стоимость при постоянной цене
длина прямоугольника и его площадь при постоянной ширине
объём выполненной работы и затраченное на неё время при постоянной производительности труда
производительность труда и объём выполненной работы при постоянном времени
длина пути, проходимого равномерно движущимся телом, и время его движения
скорость и длина пути при постоянном времени

Прямо пропорциональные величины
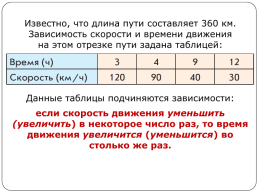
Пример За 2 часа машина прошла 120 км. Требуется узнать, какое расстояние она пройдёт за 6 ч, если скорость останется неизменной.
способ 1
Сначала узнаем, во сколько раз увеличится время движения: 6 : 2 = 3 раза.
Следовательно, путь так же увеличится в три раза: 120 · 3 = 360 (км).

Прямо пропорциональные величины
Пример За 2 часа машина прошла 120 км. Требуется узнать, какое расстояние она пройдёт за 6 ч, если скорость останется неизменной.
способ 2
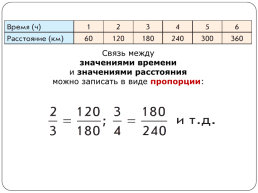
Условие этой задачи можно записать так:
Одинаково направленные стрелки показывают, что величины прямо пропорциональны, то есть отношение значений расстояния 120 : х равно отношению соответствующих значений времени 2 : 6.

Прямо пропорциональные величины
Пример За 2 часа машина прошла 120 км. Требуется узнать, какое расстояние она пройдёт за 6 ч, если скорость останется неизменной.
Решение
Составим пропорцию: .
Теперь решим её:

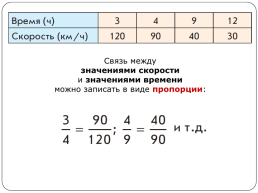
Связь между значениями скорости и значениями времени можно записать в виде пропорции:

Определение обратно пропорциональных величин
Если две величины связаны между собой так, что с увеличением (уменьшением) одной в несколько раз вторая уменьшается (увеличивается) во столько же раз, то такие величины называются обратно пропорциональными.

Обратно пропорциональные величины
Если две величины обратно пропорциональны, то отношение любых двух значений первой величины равно обратному отношению соответствующих значений второй величины.
Пример
– при неизменном расстоянии

Обратно пропорциональные величины
Примеры обратно пропорциональных величин:
количество товара и его цена при одинаковой стоимости покупки
скорость и время движения равномерно движущегося объекта при одинаковой длине пути
производительность труда и время работы при одинаковом объёме работы
число рабочих и время выполнения ими заданной работы при одинаковой производительности труда всех рабочих
величина дроби и её знаменатель при постоянном числителе

Обратно пропорциональные величины
Пример Машина затратила 2 часа на движение по некоторому участку пути со скоростью 50 км/ч. Требуется узнать, за какое время она пройдёт этот же участок пути, если её скорость будет 100 км/ч.
Метод 1
Сначала узнаем, во сколько раз увеличится скорость движения: 100 : 50 = 2 раза.
Следовательно, время движения уменьшится в 2 раза и станет равным: 2 : 2 = 1 ч.

Обратно пропорциональные величины
Пример Машина затратила 2 часа на движение по некоторому участку пути со скоростью 50 км/ч. Требуется узнать, за какое время она пройдёт этот же участок пути, если её скорость будет 100 км/ч.
способ 2
Условие этой задачи можно записать так:
Противоположно направленные стрелки показывают, что величины обратно пропорциональны, то есть отношение значений скорости 50 : 100 равно обратному отношению соответствующих значений времени х : 2.

Обратно пропорциональные величины
Пример Машина затратила 2 часа на движение по некоторому участку пути со скоростью 50 км/ч. Требуется узнать, за какое время она пройдёт этот же участок пути, если её скорость будет 100 км/ч.
Решение
Составим пропорцию: .
Найдём неизвестный член пропорции:

Алгоритм решения задач на пропорции.
1) Искомую величину обозначить за x. 2) По условию составить таблицу. 3) Указать вид зависимости, поставив стрелочки. 4) Записать пропорцию, следуя по стрелочкам. 5) Решить пропорцию. 6) Записать ответ.