Презентация - Максимум и минимум функции
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 98%
- Слайдов: 26
- Просмотров: 1359
- Скачиваний: 170
- Размер: 0.24 MB
- Онлайн: Да
- Формат: ppt / pptx
Примеры похожих презентаций
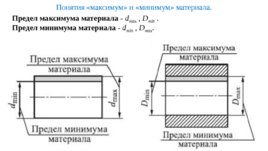 Понятия «максимум» и «минимум» материала
Понятия «максимум» и «минимум» материала Функциональные разновидности языка
Функциональные разновидности языка Причины возникновения, виды и функции денег
Причины возникновения, виды и функции денег Построение и исследование графиков функций с использованием программного обеспечения компьютеров
Построение и исследование графиков функций с использованием программного обеспечения компьютеров Белки (строение и функции)
Белки (строение и функции) Белки (свойства и функции)
Белки (свойства и функции) Обратные тригонометрические функции (10 класс)
Обратные тригонометрические функции (10 класс)
Слайды и текст этой онлайн презентации
Слайд 1

Максимум и минимум функции
Слайд 2
Повторение
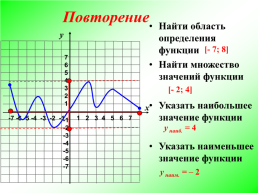
Найти область определения функции Найти множество значений функции Указать наибольшее значение функции Указать наименьшее значение функции
у
[- 7; 8]
7 6 5 4 3 2 1
[- 2; 4]
х
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
-1 -2 -3 -4 -5 -6 -7
у наиб. = 4
у наим. = – 2
Найти область определения функции Найти множество значений функции Указать наибольшее значение функции Указать наименьшее значение функции
у
[- 7; 8]
7 6 5 4 3 2 1
[- 2; 4]
х
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
-1 -2 -3 -4 -5 -6 -7
у наиб. = 4
у наим. = – 2
Слайд 3
Повторение
у
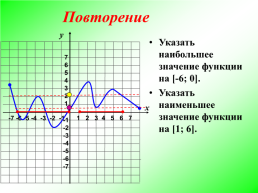
Указать наибольшее значение функции на [-6; 0]. Указать наименьшее значение функции на [1; 6].
7 6 5 4 3 2 1
х
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
-1 -2 -3 -4 -5 -6 -7
у
Указать наибольшее значение функции на [-6; 0]. Указать наименьшее значение функции на [1; 6].
7 6 5 4 3 2 1
х
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
-1 -2 -3 -4 -5 -6 -7
Слайд 4

Повторение
Геометрический смысл производной.
Производная функции в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Геометрический смысл производной.
Производная функции в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.
Слайд 5
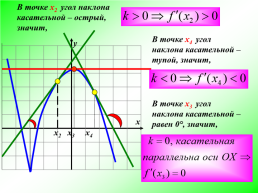
В точке х2 угол наклона касательной – острый, значит,
В точке х4 угол наклона касательной – тупой, значит,
у
В точке х3 угол наклона касательной – равен 0°, значит,
х
х2 х3 х4
В точке х4 угол наклона касательной – тупой, значит,
у
В точке х3 угол наклона касательной – равен 0°, значит,
х
х2 х3 х4
Слайд 6

Максимум функции на отрезке
Определение Говорят, что функция у = f(х) принимает на отрезке [a; b] наибольшее значение в точке х0 є [a;b], если для любого х є [a;b] выполняется f(x0) ≥ f(x). Наибольшее значение называют максимумом функции на отрезке [a;b], а точку х0 – точкой максимума Обозначение:
Определение Говорят, что функция у = f(х) принимает на отрезке [a; b] наибольшее значение в точке х0 є [a;b], если для любого х є [a;b] выполняется f(x0) ≥ f(x). Наибольшее значение называют максимумом функции на отрезке [a;b], а точку х0 – точкой максимума Обозначение:
Слайд 7

Минимум функции на отрезке.
Определение Говорят, что функция у = f(х) принимает на отрезке [a; b] наименьшее значение в точке х0 є [a;b], если для любого х є [a;b] выполняется f(x0) ≤ f(x). Наименьшее значение называют минимумом функции на отрезке [a;b], а точку х0 – точкой минимума Обозначение:
Определение Говорят, что функция у = f(х) принимает на отрезке [a; b] наименьшее значение в точке х0 є [a;b], если для любого х є [a;b] выполняется f(x0) ≤ f(x). Наименьшее значение называют минимумом функции на отрезке [a;b], а точку х0 – точкой минимума Обозначение:
Слайд 8
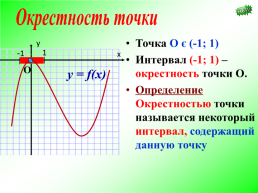
Окрестность точки
Точка О є (-1; 1) Интервал (-1; 1) – окрестность точки О. Определение Окрестностью точки называется некоторый интервал, содержащий данную точку
y
-1
x
О
у = f(х)
Слайд 9
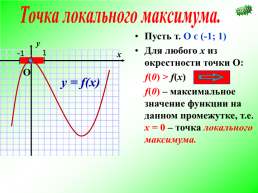
Точка локального максимума.
Пусть т. О є (-1; 1) Для любого х из окрестности точки О: f(0) > f(х) f(0) – максимальное значение функции на данном промежутке, т.е. х = 0 – точка локального максимума.
y
-1
x
О
у = f(х)
Слайд 10
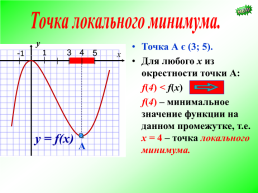
Точка локального минимума.
y
Точка А є (3; 5). Для любого х из окрестности точки А: f(4) < f(х) f(4) – минимальное значение функции на данном промежутке, т.е. х = 4 – точка локального минимума.
-1
x
у = f(х)
А
Слайд 11
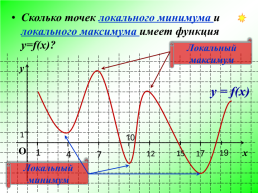
Сколько точек локального минимума и локального максимума имеет функция у=f(х)?
Локальный максимум
y
у = f(х)
Локальный минимум
Слайд 12
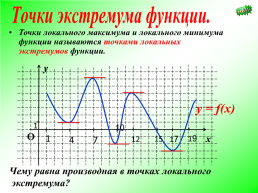
Точки экстремума функции.
Точки локального максимума и локального минимума функции называются точками локальных экстремумов функции.
y
у = f(х)
Чему равна производная в точках локального экстремума?
Слайд 13
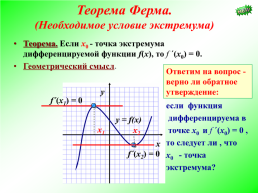
Теорема Ферма. (Необходимое условие экстремума)
Теорема. Если х0 - точка экстремума дифференцируемой функции f(х), то f ´(х0) = 0. Геометрический смысл.
Ответим на вопрос - верно ли обратное утверждение:
y
f´(х1) = 0
если функция дифференцируема в точке х0 и f ´(х0) = 0 , то следует ли , что х0 - точка экстремума?
у = f(х)
x1
x2
x
f´(х2) = 0
Теорема. Если х0 - точка экстремума дифференцируемой функции f(х), то f ´(х0) = 0. Геометрический смысл.
Ответим на вопрос - верно ли обратное утверждение:
y
f´(х1) = 0
если функция дифференцируема в точке х0 и f ´(х0) = 0 , то следует ли , что х0 - точка экстремума?
у = f(х)
x1
x2
x
f´(х2) = 0
Слайд 14
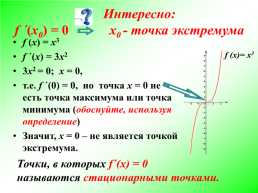
Интересно: f ´(х0) = 0 х0 - точка экстремума
f (х) = х3 f ´(х) = 3х2 3х2 = 0; х = 0, т.е. f ´(0) = 0, но точка х = 0 не есть точка максимума или точка минимума (обоснуйте, используя определение) Значит, х = 0 – не является точкой экстремума.
f (х)= х3
Точки, в которых f´(х) = 0 называются стационарными точками.
f (х) = х3 f ´(х) = 3х2 3х2 = 0; х = 0, т.е. f ´(0) = 0, но точка х = 0 не есть точка максимума или точка минимума (обоснуйте, используя определение) Значит, х = 0 – не является точкой экстремума.
f (х)= х3
Точки, в которых f´(х) = 0 называются стационарными точками.
Слайд 15

Задача №1
Найти наибольшее и наименьшее значение функции f (х) = х3 - 3х2 на [-1; 4]
Решение.
3) f (-1) = (-1)3 – 3∙(-1) 2=
- 4
1) f ´ (х) = 3х2 - 6х
f (4) = 43 – 3∙42=
f (0) =
2) 3х2 – 6х = 0
- 4
f (2) = 23 – 3∙22=
3х (х - 2) =0
x = 0 и х - 2 = 0
х = 2
Найти наибольшее и наименьшее значение функции f (х) = х3 - 3х2 на [-1; 4]
Решение.
3) f (-1) = (-1)3 – 3∙(-1) 2=
- 4
1) f ´ (х) = 3х2 - 6х
f (4) = 43 – 3∙42=
f (0) =
2) 3х2 – 6х = 0
- 4
f (2) = 23 – 3∙22=
3х (х - 2) =0
x = 0 и х - 2 = 0
х = 2
Слайд 16

Задача №2
Найти максимум и минимум функции f(x)= |x-2| на отрезке [0; 6]
В точке х = 2 функция не имеет производной (см. П.4.1)
Решение.
y
f(х)=|x-2|
x
Определение. Точки, в которых производная функции равна нулю или не существует, называют критическими точками этой функции.
Найти максимум и минимум функции f(x)= |x-2| на отрезке [0; 6]
В точке х = 2 функция не имеет производной (см. П.4.1)
Решение.
y
f(х)=|x-2|
x
Определение. Точки, в которых производная функции равна нулю или не существует, называют критическими точками этой функции.
Слайд 17

Ответьте на вопросы.
Что называется максимумом функции на отрезке? Что называется минимумом функции на отрезке? Что называется локальным минимумом? Локальным максимумом? Какие точки называются точками экстремума? Чему равна производная в точке экстремума? Верно ли обратное утверждение? Как называются точки, в которых производная функции равна нулю? Какие точки называются критическими точками функции?
Слайд 18

Проверь себя
(пронумеруй задания 1 – 7, запиши ответы и сверь их с ответами, приведёнными в таблице на последнем слайде)
Слайд 19
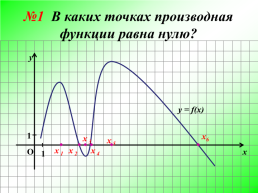
№1 В каких точках производная функции равна нулю?
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
х6
х 3
х 5
●
●
●
●
●
●
O
х 1
х 2
х 4
x
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
х6
х 3
х 5
●
●
●
●
●
●
O
х 1
х 2
х 4
x
Слайд 20
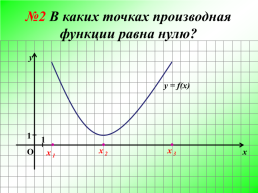
№2 В каких точках производная функции равна нулю?
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
●
●
●
O
х 2
х 3
x
х 1
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
●
●
●
O
х 2
х 3
x
х 1
Слайд 21
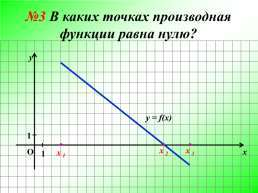
№3 В каких точках производная функции равна нулю?
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
●
●
●
O
х 2
х 3
x
х 1
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
●
●
●
O
х 2
х 3
x
х 1
Слайд 22
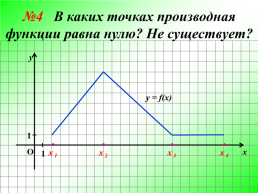
№4 В каких точках производная функции равна нулю? Не существует?
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
●
●
●
●
O
x
х 1
х 2
х 3
х 4
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
●
●
●
●
O
x
х 1
х 2
х 3
х 4
Слайд 23
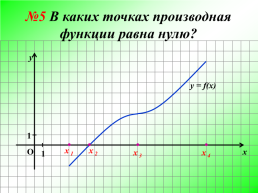
№5 В каких точках производная функции равна нулю?
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
●
●
●
●
O
х 1
х 2
x
х 3
х 4
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
●
●
●
●
O
х 1
х 2
x
х 3
х 4
Слайд 24
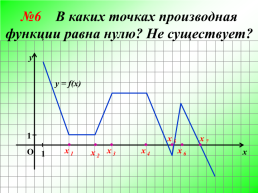
№6 В каких точках производная функции равна нулю? Не существует?
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
х 5
х 7
●
●
●
●
●
●
●
O
х 1
х 3
х 4
х 6
x
х 2
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
х 5
х 7
●
●
●
●
●
●
●
O
х 1
х 3
х 4
х 6
x
х 2
Слайд 25
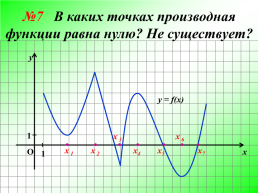
№7 В каких точках производная функции равна нулю? Не существует?
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
х 3
х 6
●
●
●
●
●
●
●
O
х 1
х 2
х4
х5
х7
x
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
.............................
y
у = f(х)
х 3
х 6
●
●
●
●
●
●
●
O
х 1
х 2
х4
х5
х7
x
Слайд 26
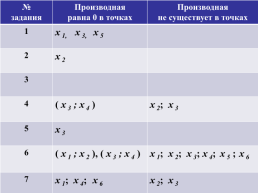
№ задания.Производная равна 0 в точках.Производная не существует в точках
1.х 1, х 3, х 5.
2.х 2.
3..
4.( х 3 ; х 4 ).х 2; х 3
5.х 3.
6.( х 1 ; х 2 ), ( х 3 ; х 4 ).х 1; х 2; х 3; х 4; х 5 ; х 6
7.х 1; х 4; х 6.х 2; х 3
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
