Презентация - Взаимное расположение двух прямых в пространстве

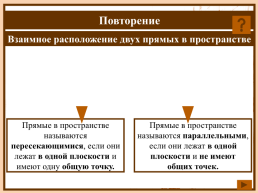
Взаимное расположение двух прямых в пространстве
Прямые в пространстве называются пересекающимися, если они лежат в одной плоскости и имеют одну общую точку.
Прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.

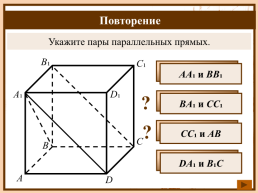
Укажите пары параллельных прямых.
В₁
С₁
AA₁ и ВB₁
A₁
D₁
?
ВA₁ и СС₁
?
СС₁ и АВ
С
В
DA₁ и В₁C
A
D

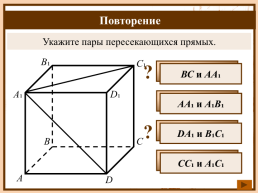
Укажите пары пересекающихся прямых.
В₁
С₁
?
ВС и AA₁
A₁
D₁
AA₁ и A₁B₁
?
DA₁ и B₁C₁
В
С
СС₁ и А₁C₁
A
D

Определение
Две прямые называются скрещивающимися, если не существует такой плоскости, которая бы проходила через эти прямые.

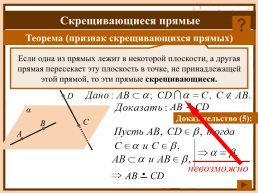
Теорема (признак скрещивающихся прямых)
Если одна из прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей этой прямой, то эти прямые скрещивающиеся.
Доказательство (5):

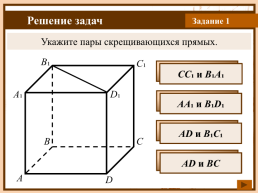
Задание 1
Укажите пары скрещивающихся прямых.
В₁
С₁
СС₁ и B₁А₁
A₁
D₁
AA₁ и B₁D₁
AD и B₁C₁
В
С
AD и BC
A
D

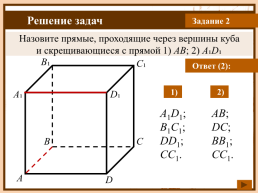
Задание 2
Назовите прямые, проходящие через вершины куба и скрещивающиеся с прямой 1) AB; 2) A₁D₁
В₁
С₁
Ответ (2):
2)
1)
A₁
D₁
A1D1; B1C1; DD1; CC1.
AB; DC; BB1; CC1.
В
С
A
D

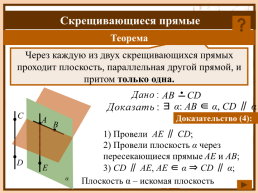
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство (4):
1) Провели AE ∥ CD;
2) Провели плоскость α через пересекающиеся прямые AE и АВ;
3) CD ∥ AE, AE ∈ α ⇒ CD ∥ α;
Плоскость α – искомая плоскость

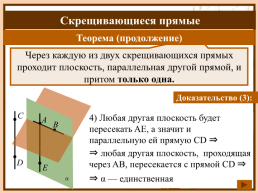
Теорема (продолжение)
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство (3):
4) Любая другая плоскость будет пересекать AE, а значит и параллельную ей прямую CD ⇒
⇒ любая другая плоскость, проходящая через AB, пересекается с прямой CD ⇒
⇒ α — единственная

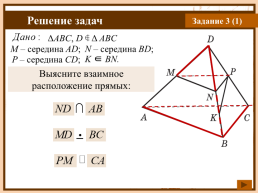
Задание 3 (1)
ΔABC, D ∉ Δ ABC
M – середина AD;
N – середина BD;
K ∈ BN.
P – середина CD;
Выясните взаимное расположение прямых:

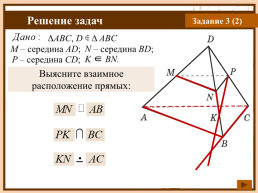
Задание 3 (2)
ΔABC, D ∉ Δ ABC
M – середина AD;
N – середина BD;
K ∈ BN.
P – середина CD;
Выясните взаимное расположение прямых:

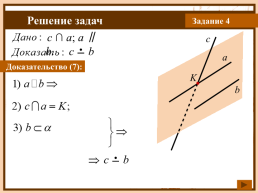
Задание 4
c ∩ a; a ∥ b.
c
a
Доказательство (7):
K
b

Фон презентации
Презентации к урокам