Слайды и текст этой онлайн презентации
Слайд 1
Методическая разработка Савченко Е.М.
МОУ гимназия №1, г. Полярные Зори, Мурманской обл.
Признак перпендикулярности
прямой и плоскости
Геометрия 10
Слайд 2
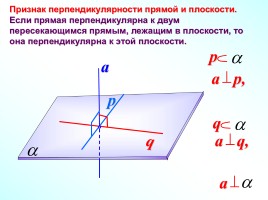
Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Слайд 3
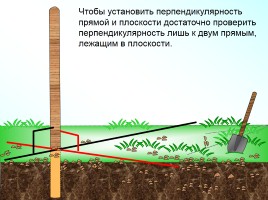
Чтобы установить перпендикулярность прямой и плоскости достаточно проверить перпендикулярность лишь к двум прямым, лежащим в плоскости.
Слайд 5
О
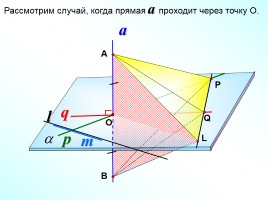
Рассмотрим случай, когда прямая a проходит через точку О.
Слайд 6
О
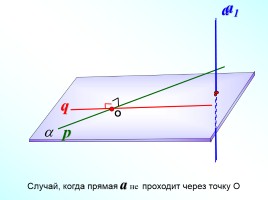
Случай, когда прямая a не проходит через точку О
Слайд 7
A
O
В
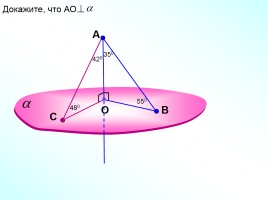
Докажите, что АО
С
С
350
550
420
480
Слайд 8
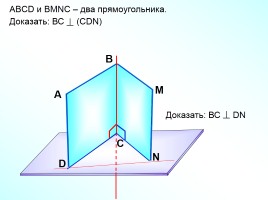
ABCD и ВMNС – два прямоугольника.
Доказать: ВС (СDN)
А
В
С
D
M
N
Слайд 9
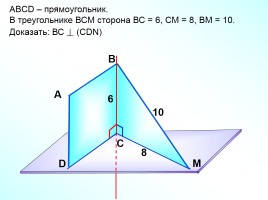
ABCD – прямоугольник.
В треугольнике ВСМ сторона ВС = 6, СМ = 8, ВМ = 10.
Доказать: ВС (СDN)
А
В
С
D
M
6
8
10
Слайд 10
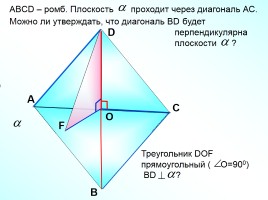
ABCD – ромб. Плоскость проходит через диагональ АС. Можно ли утверждать, что диагональ ВD будет
перпендикулярна
плоскости ?
А
В
С
D
О
Слайд 11
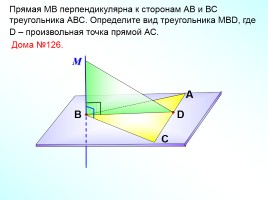
Прямая МВ перпендикулярна к сторонам АВ и ВС треугольника АВС. Определите вид треугольника МВD, где D – произвольная точка прямой АС.
А
С
В
Дома №126.
Слайд 12
В
М
O
С
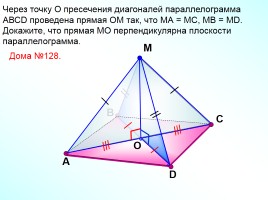
Через точку О пресечения диагоналей параллелограмма АВСD проведена прямая ОМ так, что МА = МС, МВ = МD. Докажите, что прямая МО перпендикулярна плоскости параллелограмма.
А
D
Дома №128.
Слайд 13
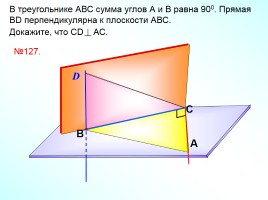
В треугольнике АВС сумма углов А и В равна 900. Прямая ВD перпендикулярна к плоскости АВС.
Докажите, что СD АС.
C
A
B
№127.
Слайд 14
D
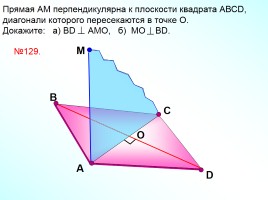
Прямая АМ перпендикулярна к плоскости квадрата АВСD, диагонали которого пересекаются в точке О.
Докажите: а) ВD АМО, б) МО ВD.
A
C
B
О
№129.
Слайд 15
А
М
D
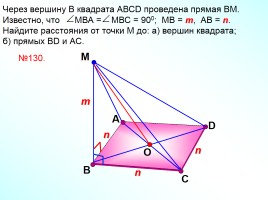
Через вершину В квадрата АВСD проведена прямая ВМ. Известно, что МВА = МВС = 900; МВ = m, АВ = n. Найдите расстояния от точки М до: а) вершин квадрата;
б) прямых ВD и АС.
В
С
n
m
n
n
№130.
Слайд 16
С
B
A
D
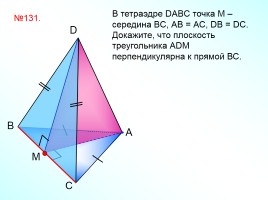
В тетраэдре DABC точка М – середина BС, АB = АС, DВ = DC.
Докажите, что плоскость треугольника АDМ перпендикулярна к прямой ВС.
M
№131.
Слайд 17
D
А
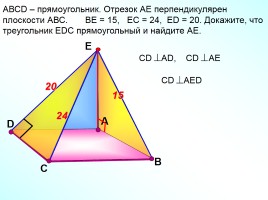
АВСD – прямоугольник. Отрезок АЕ перпендикулярен плоскости АВС. ВЕ = 15, ЕС = 24, ЕD = 20. Докажите, что треугольник ЕDС прямоугольный и найдите АЕ.
C
В
Е
Слайд 18
С
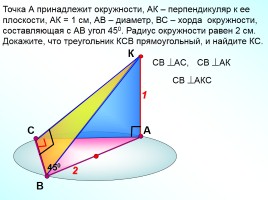
Точка А принадлежит окружности, АК – перпендикуляр к ее плоскости, АК = 1 см, АВ – диаметр, ВС – хорда окружности, составляющая с АВ угол 450. Радиус окружности равен 2 см. Докажите, что треугольник КСВ прямоугольный, и найдите КС.
В
А
2
1
450
Слайд 19
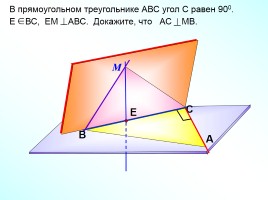
В прямоугольном треугольнике АВС угол С равен 900.
Е ВС, ЕМ АВС. Докажите, что АС МВ.
C
A
B
Е
Слайд 21
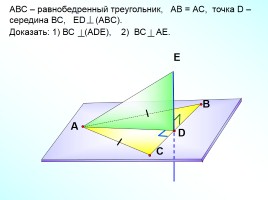
АВС – равнобедренный треугольник, АВ = АС, точка D – середина ВС, ЕD (ABC).
Доказать: 1) ВС (АDЕ), 2) ВС АЕ.
В
С
А
Слайд 22
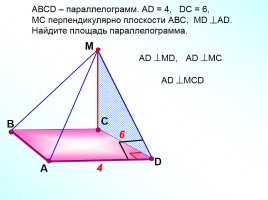
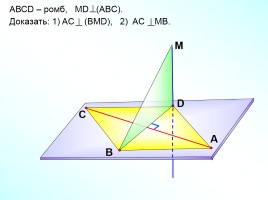
АВСD – ромб, МD (ABC).
Доказать: 1) AС (BMD), 2) AС MB.
D
С
А
B
Слайд 23
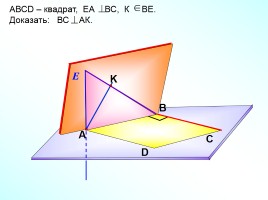
АВСD – квадрат, ЕА ВС, К ВЕ.
Доказать: ВС АК.
С
А
D
В
 Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Прямоугольный треугольник. Признаки равенства прямоугольных треугольников
Прямоугольный треугольник. Признаки равенства прямоугольных треугольников Взаимное положение прямой и плоскости
Взаимное положение прямой и плоскости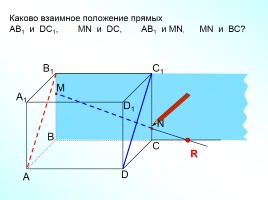 Параллельность прямой и плоскости
Параллельность прямой и плоскости Перпендикулярность плоскостей - Параллелепипед
Перпендикулярность плоскостей - Параллелепипед Параллельные плоскости - Признак параллельности двух плоскостей
Параллельные плоскости - Признак параллельности двух плоскостей Угол между прямой и плоскостью
Угол между прямой и плоскостью