Презентация - Урок алгебры в 9 классе по теме «Неравенства»

Урок алгебры в 9 классе по теме: «Неравенства».
Урок разработала и провела Малиновская Галина Анатольевна, учитель математики МБОУ «СОШ № 2» г. Алексина, Тульской области, 2015 год.

Тип урока: обобщение. Цели урока:
Образовательные: а). Обобщение и систематизация знаний учащихся по теме «Неравенства». б). Закрепление и решение заданий по данной теме. в). Выработка умения анализировать, выделять главное. Развивающие: а). Развитие памяти, внимания, логического мышления. б). Развитие навыков самоконтроля при выполнении самостоятельной работы. Воспитывающие: а). Воспитание объективной самооценки при выполнении заданий. б). Воспитание умения выдерживать регламент времени, отведенного на решение каждого задания. в). Привитие интереса к предмету.

Повторение основных понятий.
Линейное неравенство – неравенство вида ах+в>0 (ах+в<0), где а и в – любые числа, а≠0. Квадратное неравенство – неравенство вида ах2+вх+с>0 (ах2+вх +с<0), где а≠0.

Равносильные преобразования неравенств.
Правило 1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, не меняя при этом знак неравенства. Правило 2. Обе части неравенства можно умножить или разделить на одно и то же положительное число, не меняя при этом знак неравенства.

Основные правила решения неравенств.
Правило 3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.

Алгоритм решения квадратного неравенства ах2+вх+с>0
Определить, куда (вверх или вниз) направлены ветви параболы, служащей графиком функции у=ах2+вх+с. Найти точки пересечения параболы с ось Х, решив уравнение ах2+вх+с=0. Отметить найденные корни на оси Х и сделать эскиз графика. С помощью полученной геометрической модели определить, на каких промежутках оси Х ординаты графика положительны (отрицательны) и включить эти промежутки в ответ.

Решение квадратных неравенств методом интервалов.
Разложить квадратный трехчлен на множители, воспользовавшись формулой ах2+вх+с=а(х-х1)(х-х2). Отметить на числовой прямой корни квадратного трехчлена. Определить на каких промежутках трехчлен имеет положительный или отрицательный знак. Учитывая знак неравенства, включить нужные промежутки в ответ.

Решение дробно-рациональных неравенств методом интервалов
1. Привести данное неравенство к виду 2. Разложить числитель и знаменатель дроби на множители; 3. Нанести на числовую ось числа, при которых каждый множитель равен нулю и разделить числовую ось на промежутки; 4.Изобразить выбитыми те точки, которые не являются решением неравенства; 5. Выяснить знаки промежутков; 6. Выбрать ответ.

Решение неравенств
1. Решить линейное неравенство: 3х – 5 ≥ 7х - 15 Ответ: (-∞; 2,5].
3х – 7х ≥ -15 + 5 Перенесите слагаемые, не забыв поменять знаки слагаемых
-4х ≥ -10 Приведите подобные слагаемые в левой и в правой частях неравенства.
х ≤ 2,5 Разделите обе части на -4, не забыв поменять знак неравенства.

Решение неравенств
2. Решить квадратное неравенство: а) х2>16 б) х2+5>0 х2-16>0 Ответ: верно при (х-4)(х+4)>0 любом значении Х. + - + в) х2+ 5<0 -4 4 х Ответ: не имеет Ответ:(-∞;-4)U(4;+∞) решений.

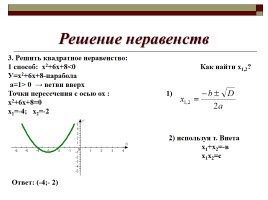
Решение неравенств
3. Решить квадратное неравенство: 1 способ: х2+6х+8<0 Как найти х1,2? У=х2+6х+8-парабола а=1> 0 → ветви вверх Точки пересечения с осью ох : 1) х2+6х+8=0 х1=-4; х2=-2 2) используя т. Виета х1+х2=-в х1х2=с Ответ: (-4;- 2)

Решение неравенств
Решить квадратное неравенство: 2 способ (метод интервалов): х2+6х+8<0 Рассмотрим функцию у = х2+6х+8 Нули функции х2+6х+8=0 х1=-4; х2=-2 (x+4)(x+2)<0 + - + -4 -2 x Ответ: -4

Самостоятельная работа. Решить неравенства:
1 вариант 2 вариант а)5х+4 < 9х-12 а)7х-11≥ 10х-8 б)х2+ 3х-4≥ 0 б)х2-5х-36<0 в)(х+5)(х-7)<0 в)(х+1)(х-4)>0 г)(х-1)2(2х-1)(х+2)≤ 0 г)(х-2)2(5х+4)(х-7)≥0 д) д)

Проверь себя:
1 Вариант 2 Вариант 1. х>4 1. x≤-3 2. x≤-4; x≥1 2. -45 5. x≤-8: -2

Используемая литература:
«Алгебра 9 класс», часть 1, учебник, под редакцией А.Г. Мордковича, Мнемозина, 2013 г. «Алгебра 9 класс», часть 2, задачник, под редакцией А.Г. Мордковича, Мнемозина, 2013 г. «Самостоятельные работы алгебра 9» под редакцией Л.А. Александрова, Мнемозина,2013г. «Типовые тестовые задания для подготовки к государственной (итоговой) аттестации в форме ОГЭ», под редакцией И.В. Ященко, 2016 г.