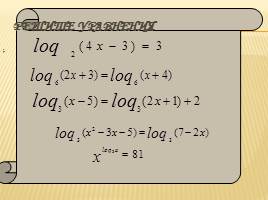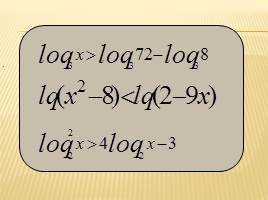Презентация - Решение логарифмических уравнений и неравенств

Решение логарифмических уравнений и неравенств. Учитель математики МБОУ СОШ с. Березовка 1-я Портнова С.Ю.

Логарифмические уравнения
Уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими.

Решение уравнений, содержащих неизвестное под знаком логарифма, основано на следующих теоремах:

Методы решения ЛУ: Вид уравнения
1.Применение определения логарифма
2.Введение новой переменной
3. Приведение к одному и тому же основанию
4. Метод потенцирования
5 Метод логарифмирования обеих частей уравнения
6. Функционально-графический метод

Выбери метод решения уравнения

Решите уравнения
;.

Найти корни уравнения
;.

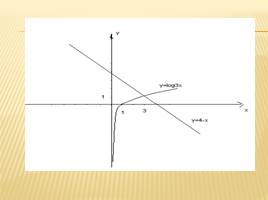
Для решения ЛУ графическим методом надо построить в одной и той же системе координат графики функций, стоящих в левой и правой частях уравнения и найти абсциссу их точки пересечения
Найти корни уравнения Так как функция у= log3 х возрастающая, а функция у =4-х убывающая на (0; + ∞ ),то заданное уравнение на этом интервале имеет один корень.

Логарифмические неравенства
Решение неравенств, содержащих неизвестное под знаком логарифма, основано на следующих теоремах:

Решите неравенства
1

.

.

Логарифмическая «комедия 2>3»
Комедия начинается с неравенства, бесспорно правильного. Затем следует преобразование тоже не внушающее сомнения Большему числу соответствует больший логарифм, если функция возрастает, значит, После сокращения на Имеем 2>3. В чем ошибка этого доказательства?