Презентация - Функции и их графики

Функции и их графики

Содержание
Теоретические сведения о функциях Преобразование графиков функций Элементарные функции и их графики Об авторе

Теоретические сведения о функциях
Понятие функции Свойства функции

Понятие функции
Функцией называют такую зависимость переменной У от переменной Х, при которой каждому значению переменной Х соответствует единственное значение переменной У. Х – независимая переменная (аргумент) У – зависимая переменная (значение функции) Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: у = f(х)

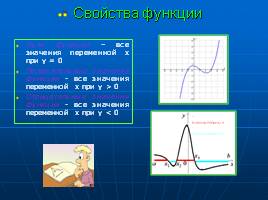
Свойства функции
Нули функции – все значения переменной х при у = 0 Положительные значения функции - все значения переменной х при у > 0 Отрицательные значения функции - все значения переменной х при у < 0

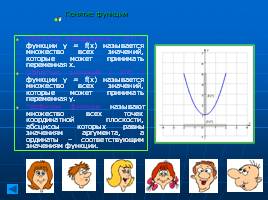
Областью определения ( D(f) ) функции у = f(х) называется множество всех значений, которые может принимать переменная х. Областью значений ( E(f) ) функции у = f(х) называется множество всех значений, которые может принимать переменная у. Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
Понятие функции

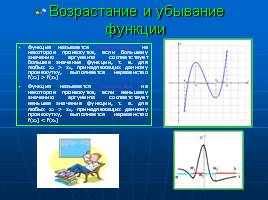
Возрастание и убывание функции
Функция называется возрастающей на некотором промежутке, если большему значению аргумента соответствует большее значение функции, т. е. для любых х2 > х1, принадлежащих данному промежутку, выполняется неравенство f(х2) > f(х1) Функция называется убывающей на некотором промежутке, если меньшему значению аргумента соответствует меньшее значение функции, т. е. для любых х2 > х1, принадлежащих данному промежутку, выполняется неравенство f(х2) < f(х1)

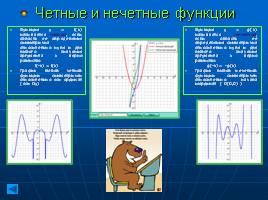
Четные и нечетные функции
Функция у = f(x) называется четной, если область ее определения симметрична относительно нуля и для любого значения аргумента x верно равенство f(-x) = f(x) График любой четной функции симметричен относительно оси ординат ( оси Оу)
Функция у = g(x) называется нечетной, если область ее определения симметрична относительно нуля и для любого значения аргумента x верно равенство g(-x) = -g(x) График любой нечетной функции симметричен относительно начала координат ( О(0,0) )

Преобразование графиков функций
 Функция Преобразование графиков функции
у = f(х)+а Параллельный перенос вдоль оси OY на а единиц вверх, если а>0, и на |а| единиц вниз, если а<0.
у = f (х-а) Параллельный перенос вдоль оси OX на a единиц вправо, если a > 0, на |a| единиц влево, если a < 0.
у = kf(х) Растяжение вдоль оси OY относительно оси OX в k раз, если k > 1, и сжатие в 1/k раз, если 0 < k < 1.
у = f(kx) Сжатие вдоль оси OX относительно оси OY в k раз, если k > 1, и растяжение в 1/k раз, если 0 < k < 1.
у = -f(х) Симметричное отражение относительно оси OX
у = |f(х)| Часть графика, расположенная ниже оси OX, симметрично отражается относительно этой оси, остальная его часть остается без изменения.
у = f(-х) Симметричное отражение относительно оси OY.
у = f(|х|) Часть графика, расположенная в области x ≥ 0, остается без изменения, а его часть для области x ≤ 0 заменяется симметричным отображением относительно оси OY части графика для x і≥0.
Посмотреть рисунки преобразований

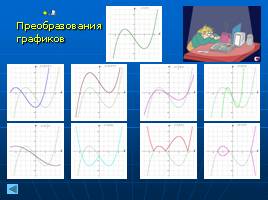
Преобразования графиков

Элементарные функции и их графики
Линейная функция Прямая пропорциональность Обратная пропорциональность Квадратичная функция Кубическая функция

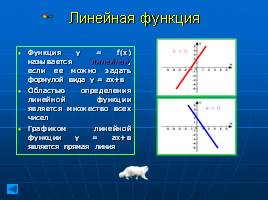
Линейная функция
Функция у = f(х) называется линейной, если ее можно задать формулой вида у = ах+в Областью определения линейной функции является множество всех чисел Графиком линейной функции у = ах+в является прямая линия

Прямая пропорциональность
Функция у = f(x) называется прямой пропорциональностью, если ее можно задать формулой вида у = kx k – коэффициент пропорциональности Областью определения прямой пропорциональности у = kx является множество всех чисел Графиком прямой пропорциональности у = kx является прямая

Обратная пропорциональность
Обратной пропорциональностью называется функция, которую можно задать формулой вида у = , k ≠ 0 Область определения обратной пропорциональности состоит из всех чисел, кроме нуля Область значений обратной пропорциональности состоит из всех чисел, кроме нуля Графиком обратной пропорциональности у = является кривая, называемая гиперболой, состоящей из двух отдельных частей, симметричных относительно начала координат

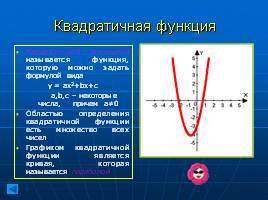
Квадратичная функция
Квадратичной функцией называется функция, которую можно задать формулой вида у = ах2+bх+с a,b,с – некоторые числа, причем а≠0 Областью определения квадратичной функции есть множество всех чисел Графиком квадратичной функции является кривая, которая называется параболой

Преобразования графиков квадратичной функции
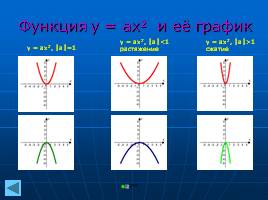
у = ах2 у = ах2+n у = а(х-m)2 у = а(х-m)2+n

Функция у = ax2 и её график

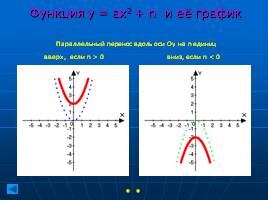
Функция у = ax2 + n и её график

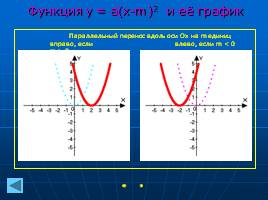
Функция у = a(x-m)2 и её график

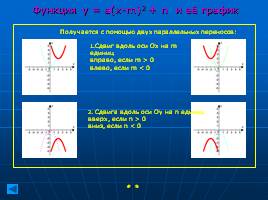
Функция у = a(x-m)2 + n и её график

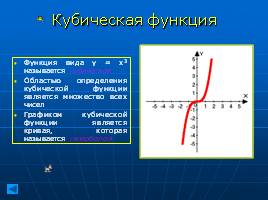
Кубическая функция
Функция вида у = х3 называется кубической Областью определения кубической функции является множество всех чисел Графиком кубической функции является кривая, которая называется гиперболой

Об авторе