Презентация - Квадратные уравнения - методы решения

Квадратные уравнения: методы решения.
Выполнила учитель математики высшей категории МОБУ«Солнечная СОШ» Зайцева С.Л.
2013 г.

«Уравнение - это золотой ключ, открывающий все математические сезамы». С. Коваль.

ПЛАН УРОКА
1. Теоретическая разминка. 2. Энциклопедия квадратных уравнений. 3. Думающий колпак. 4. Историческая справка. 5. Копилка ценных мыслей. 6. Домашнее задание.

Сформулируйте определение квадратного уравнения. 2. Объясните, в чём заключается смысл ограничения в определении квадратного уравнения (а ≠ 0). 3. Перечислите виды квадратных уравнений. 4. Какое квадратное уравнение называется неполным? Приведите пример. 5. Какое квадратное уравнение называется приведённым? Приведите пример. 6. Способы решения полного квадратного уравнения?
Вопросы теоретической разминки:
подробнее
подробнее

Специальные методы:
1. Метод выделения квадрата двучлена. 2. Метод «переброски» старшего коэффициента. 3. На основании теорем.

ДУМАЮЩИЙ КОЛПАК
Большим и указательным пальцами мягко оттягивают назад и прижимают, массируя, раковины ушей. УЧЕБНЫЕ ИНСТРУКЦИИ • Держите голову прямо, чтобы подбородку было удобно. • Упражнение повторяют трижды или более раз.

№ уравнения 1 2 3 4 5 6 7 8 9 10
Слог

.

Впервые ввёл термин «квадратное уравнение» немецкий философ
- знаменитый немецкий философ, родился в 1679 г. в Бреславле, в семье простого ремесленника, изучал в Йене сначала богословие, потом математику и философию.
Кристиан Вольф.
Кристиан Вольф -

– английский математик, который ввёл термин «дискриминант».
Сильвестр Джеймс Джозеф

В 13 – 16 веках даются отдельные методы решения различных видов квадратных уравнений. Слияние этих методов произвел в 1544 году немецкий математик – Это было настоящее событие в математике.
Михаэль Штифель.

Домашнее задание

Решите уравнение 3х2 + 5х + 2 = 0: используя формулу дискриминанта – «3», двумя способами – «4», тремя способами – «5». Дополнительно. Решите уравнение (х2-х)2 - 14(х2-х) + 24 = 0 методом введения новой переменной.

Энциклопедия квадратного уравнения
подробнее

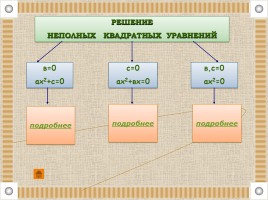
РЕШЕНИЕ НЕПОЛНЫХ КВАДРАТНЫХ УРАВНЕНИЙ
в=0 ах2+с=0
с=0 ах2+вх=0
в,с=0 ах2=0
подробнее
подробнее
подробнее

Алгоритм решения
1.Переносим с в правую часть уравнения. ах2 = -с. 2.Делим обе части уравнения на а≠0. х2= . 3.Если >0 - два решения: х1 = и х2 = - Если <0 - нет решений.
в=0 ах2+с=0

Выносим x за скобки: х (ах + в) = 0. 2. «Разбиваем» уравнение на два: x = 0, ах + в = 0. 3. Два решения: х = 0 и х = (а≠0).
Алгоритм решения
с=0 ах2+вх=0

1. Делим обе части уравнения на а≠0. х2 = 0 2. Одно решение: х = 0.
Алгоритм решения
Подведём итог!
в,с=0 ах2=0

Если < 0, то корней нет. Если > 0, то
Неполные квадратные уравнения:

D < 0
D = 0
D > 0
Корней нет

b = 2k (чётное число)

Теорема Виета

x1 и х2 – корни уравнения

x1 и х2 – корни уравнения

Суть метода: привести квадратное уравнение общего вида к неполному квадратному уравнению. Пример: х2 - 6х + 5 = 0.
Метод выделения квадрата двучлена.
подробнее

Корни квадратных уравнений и связаны соотношениями и
Пример:
Метод «переброски» старшего коэффициента.
подробнее
2х2 - 9х – 5 = 0.

На основании теорем:
Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а второй по теореме Виета равен
Если в квадратном уравнении a+c=b, то один из корней равен (-1), а второй по теореме Виета равен
Примеры:
подробнее
200х2 + 210х + 10 = 0.

Метод выделения квадрата двучлена.
(a + b)2 = a2 + 2ab + b2, (a - b)2 = a2 - 2ab + b2.
Решим уравнение х2 - 6х + 5 = 0. х2 - 6х + 5 = 0. (х -3)2 – 4 = 0. (х -3)2 = 4. х – 3 = 2; х – 3 = -2. х = 5, х =1. Ответ: 5; 1.

Метод “переброски” старшего коэффициента
ax2 + bx + c = 0 и y2+ by + ac = 0 связаны соотношениями:
Решите уравнение 2х2 - 9х – 5 = 0. у2 - 9у - 10 = 0. D>0, по теореме, обратной теореме Виета, получаем корни: -1; 10, далее возвращаемся к корням исходного уравнения: - 0,5; 5. Ответ: 5; -0,5.

Теорема 1. Если в квадратном уравнении a + b + c = 0, то один из корней равен 1, а второй по теореме Виета равен
Решите уравнение 137х2 + 20х – 157 = 0. 137х2 + 20х – 157 = 0. a = 137, b = 20, c = -157. a + b+ c = 137 + 20 – 157 =0. x1 = 1, Ответ: 1; .
.

Теорема 2. Если в квадратном уравнении a + c = b, то один из корней равен (-1), а второй по теореме Виета равен
Решите уравнение 200х2 + 210х + 10 = 0. 200х2 + 210х + 10 = 0. a = 200, b = 210, c = 10. a + c = 200 + 10 = 210 = b. х1 = -1, х2 = -
Ответ: -1; -0,05

Метод разложения на множители.
Решите уравнение 4х2 + 5х + 1 = 0. 4х2 + 5х + 1 = 0. 4х2 + 4х + х + 1 = 0. 4х(х+1) + (х+1) = 0. 4х(х + 1) = 0. Произведение двух множителей равно нулю, если хотя бы один из них равен нулю, а второй при этом не теряет смысла, или когда оба равны нулю. 4х = 0, х + 1 = 0. х = 0, х = -1. Ответ: 0; -1.

№ уравнения № метода
1 100x2 + 53x – 153 = 0
2 20x2 - 6x = 0
3 299x2 + 300x + 1 = 0
4 3x2 - 5x + 4 = 0
5 7x2 + 8x + 2 = 0
6 35x2 – 8 = 0
7 4x2 – 4x + 3 = 0
8 (x – 8)2 – (3x + 1)2 = 0
9 4(x – 1)2 + 0,5(x – 1) – 1 = 0
10 12x2 = 0
3. в=0 ах2+с=0
2. с=0 ах2+вх=0
1. в,с=0 ах2=0
4. b - нечётное ах2+bx+с=0
5. b - чётное ах2+bx+с=0
6. Теорема Виета. 7. Метод выделения квадрата двучлена. 8. Метод «переброски» старшего коэффициента. 9. Т1 или Т2. 10. Метод разложения на множители. 11. Метод введения новой переменной.

№ метода шифр
1 !
2 те
3 но
4 тик
5 нем
6 ке
7 до
8 го
9 ма
10 по
11 эт
12 ру
13 -

№ уравнения 1 2 3 4 5 6 7 8 9 10
Слог ма те ма тик нем но го по эт !
№ уравнения 1 2 3 4 5 6 7 8 9 10
Слог
Математик немного поэт. Т. Вейерштрасс